【题解】CF1633F Perfect Matching

对于树的最大匹配有一个经典的贪心算法：

• 从叶子节点开始，如果当前考虑的节点和父节点都未参与匹配就让当前考虑的节点和父亲节点匹配，即自底向上能匹配就匹配。

这启发我们使用一个 \(O(n)\) 的贪心算法 check 一棵树是否有完全匹配：

• 取树上的一片叶子，将它与它的父亲匹配，然后删除这两个顶点，重复这个过程直到只剩下孤立的顶点。如果树存在完美匹配，那么这个过程应该消除所有的顶点。

改进一下贪心算法：

• 总是挑选最深的叶子。如果存在一个完美的匹配，挑选最深的叶子将确保树始终是一棵树，不会散开，也就是说，任意时刻不存在孤立点。这意味着，当我们把叶子和它的父亲一起移除时，这个叶子是它的父亲的唯一儿子。

注意到，在算法进行的任意时刻，一个节点 \(u\) （在删除之前）的子树大小的奇偶性是固定的，因为每次移除一对点时，子树大小要么减小 \(2\)，要么不变。

考虑算法进行过程中某一个被移除的叶子节点 \(u\)，该节点会被移除意味着当前子树内除了该点以外的所有点都被移除掉了，即点 \(u\) 的子树大小为 \(1\)，因为子树大小的奇偶性是不变的所以在初始状态下点 \(u\) 子树大小一定是奇数。

同理一个点 \(u\) 会被移除，那么在该时刻点 \(u\) 的子树大小为 \(2\)，等价于在初始状态下点 \(u\) 的子树大小是偶数。

那么我们可以得出结论：一个点 \(u\) 在贪心算法中与父亲产生匹配等价于初始状态下点 \(u\) 的子树大小为奇数。

那么存在完全匹配的充分必要条件即：

• 对于每一个子树大小为偶数的点 \(u\)，存在且仅存在一个子树大小为奇数的儿子 \(v\)。

• 对于每一个子树大小为奇数的点 \(u\)，其父亲的子树大小为偶数。

那么不难得到一个必要条件，子树大小为奇数的点的个数与子树大小为偶数的点的个数相等，并且这个条件也是充分条件，充分性证明在后面。

使用轻重链剖分 + 线段树维护所有奇数点的点权和以及个数即可，复杂度 \(O(n\log^2 n)\) 。

---

如果子树大小为奇数的点的个数与子树大小为偶数的点的个数相等那么有：

• 结论 1 ：对于每一个子树大小为偶数的点 \(u\)，存在且仅存在一个子树大小为奇数的儿子 \(v\)。

• 结论 2 ：对于每一个子树大小为奇数的点 \(u\)，其父亲的子树大小为偶数。

证明：

令树 \(T=(V,E),|E|=|V|-1\)，且任意两个点 \(u,v\in V\)，连通。

对于树 \(T\) 定义 \(cnt(T,0)\) 为树 \(T\) 中子树大小为偶数的点的个数，\(cnt(T,1)\) 为树 \(T\) 中子树大小为奇数的点的个数。

引理 1 : 对于任意树 \(T\) ，\(cnt(T,1)\ge cnt(T,0)\)。

引理 1 证明：

对于任意一个树 \(T\) 中子树大小为偶数的点 \(u\) ，至少存在一个点 \(v\) 满足 ：

• \(v\) 是 \(u\) 的儿子。

• \(v\) 的子树大小为奇数。

反证，如果 \(u\) 所有儿子的子树大小均为偶数，那么 \(u\) 的子树大小为奇数。

引理 1 ，证毕。

引理 2：对于树 \(T=(V,E)\) ，若 \(|V|\) 为奇数，那么有 \(cnt(T,1)>cnt(T,0)\)。

证明：考虑树 \(T\) 根节点儿子的所有子树 \(SubTree(u),u\in son(T)\)，\(cnt(SubTree(u),1)\ge cnt(SubTree(u),0)\)，那么：

\[\sum_{u\in son(T)}cnt(SubTree(u),1)\ge\sum_{u\in son(T)}cnt(SubTree(u),0) \]

\[\sum_{u\in son(T)}cnt(SubTree(u),1)+1>\sum_{u\in son(T)}cnt(SubTree(u),0) \]

引理 2 ，证毕。

结论 2 等价命题：对于树 \(T\) ，若 \(cnt(T,0) = cnt(T,1)\)，那么不存在子树大小为奇数的点 \(u\)，其父亲的子树大小为奇数。

反正法（反证），若存在子树大小为奇数的点 \(u\)，其父亲的子树大小为奇数。

令 \(u\) 的父亲为 \(fa\)。

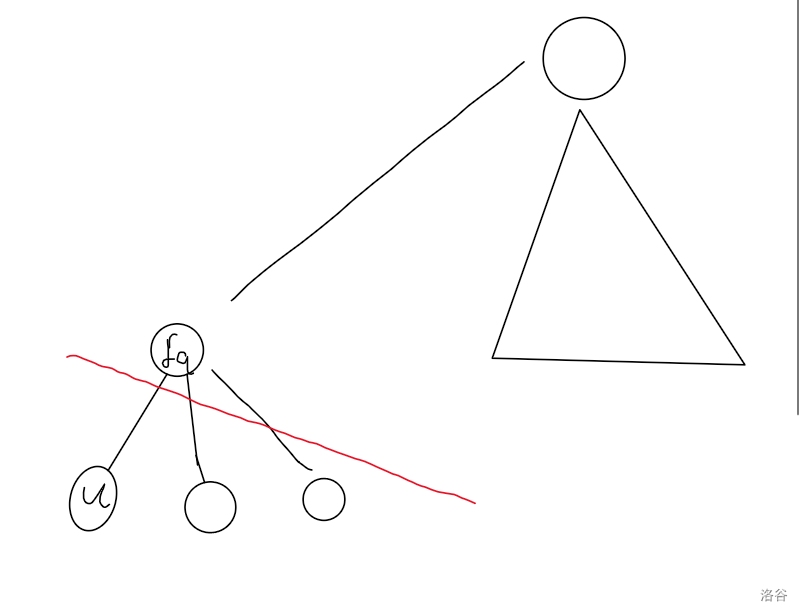
那么将树割为两部分，\(G=\{T-SubTree(fa)\}\cup \{fa\}\) 与\(G'=T-G\) 。

那么 \(cnt(G,1)\ge cnt(G,0)\)，并且在森林 \(G'\) 存在至少两棵树有奇数个点，因为引理 2，一定有：

\[cnt(G',1)>cnt(G',0) \]

进而可以推出 \(cnt(G',1)+cnt(G,1)>cnt(G,0)+cnt(G',0)\)

因为树 \(T=G\cup G'\)，且 \(cnt(T,0)=cnt(G,0)+cnt(G',0),cnt(T,1)=cnt(G',1)+cnt(G,1)\)。

所以，可以得到

\[cnt(T,1)>cnt(T,0) \]

因此，若树 \(T\) 存在子树大小为奇数的点 \(u\)，其父亲的子树大小为奇数，一定不存在 \(cnt(T,1),cnt(T,0)\)。

结论 2 证毕。

结论 1 等价命题：对于树 \(T\) ，若 \(cnt(T,0) = cnt(T,1)\)，那么不存在一个点 \(u\) ，满足 \(u\) 的子树大小为偶数，且具有多余 \(1\) 的儿子满足子树大小为奇数。

证明（反证）：若树 \(T\) 存在一个点 \(u\)，满足 \(u\) 的子树大小为偶数，且具有多余 \(1\) 的儿子满足字数大小为奇数。

令集合 \(Set(u)\) 表示 \(u\) 并上 \(u\) 的一个子树大小为奇数的儿子的子树并上所有子树大小为偶数的儿子的子树。

同样考虑将树拆成两部分，令 \(G=\{T-SubTree(u)\}\cup Set(u)\)，\(G'=T-G\)

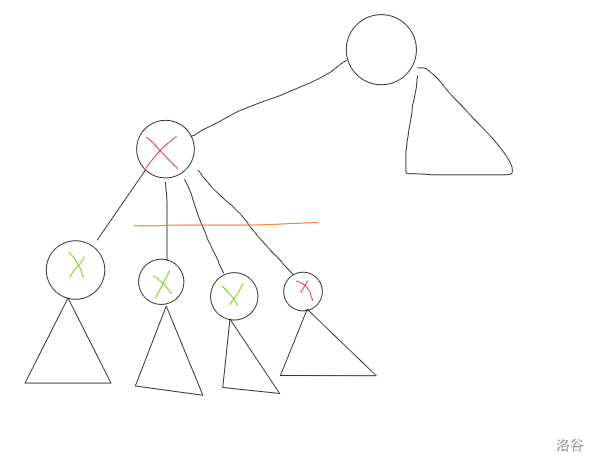
其中打绿叉的表示子树大小为奇数的点，打红叉的表示子树大小为偶数的点。

那么有 ：

\[cnt(G,1)\ge cnt(G,0) \]

因为 \(u\) 的子树大小为偶数，所以 \(G'\) 中有至少两棵子树大小为奇数的树，那么有：

\[cnt(G',1)>cnt(G',0) \]

同理，可以得出 \(cnt(T,1)>cnt(T,0)\)，因此若树 \(T\) 存在一个点 \(u\)，满足 \(u\) 的子树大小为偶数，且具有多余 \(1\) 的儿子满足子树大小为奇数，那么不可能存在 \(cnt(T,1)=cnt(T,0)\)。

结论 1 证毕。