【题解】CF1606D Red-Blue Matrix 贪心
对于任意一组的合法染色解,一定存在一种分割方案 \(cut(idx)\) (我们用 \(cut(idx)\) 表示一种分割矩形的方案,意为将矩阵分割成 \(1\sim idx\) 列,\(idx+1\sim m\) 列的分割方案),满足题目的关于颜色格子权值大小关系的限制。
因此考虑枚举分割方案 \(cut(idx)\) ,对每种分割方案尝试构造一种染色方案使其满足题目要求。
考虑题目对于切割出的左边的矩阵的限制:
- 左矩阵中所有红色元素比所有蓝色元素大。
对该限制做一个等价的转换:
- 左矩阵中红色元素的最小值大于蓝色元素的最大值。
因此,我们实际只在意切割出的矩阵每行的最小值与最大值,等价于对问题进行了一个降维。
转化后的限制即:
- \(n\) 个二元组 \((Mn,Mx)\) , 要求从中选出若干个,使得选出的每个二元组满足 \(\forall (Mn_i,Mx_i),Mn_i\) 大于任意一个不在集合中二元组的 \(Mx'\) 。
因为对于任意二元组 \((Mn,Mx)\) 有 \(Mn > Mx\) ,所以选出的每个二元组满足 \(\forall (Mn_i,Mx_i),Mn_i\) 大于任意一个不在集合中二元组的 \(Mn'\) 。
(将二维不容易确定点对相对关系的限制转化到一维容易确定相对关系的限制上。)
因此如果我们选了一个二元组 \((Mn_k,Mx_k)\) 那么所有 \((Mn_i,Mx_i),Mn_i \ge Mn_k\) 的是必选的。
因此我们将所有的二元组按 \(Mn\) 升序排序,对于任一合法的涂色方案涂红色的行一定是排序后的一个后缀。
因此,我们可以得出以下的做法:
-
枚举 \(cut(idx)\) 。
-
对于每个固定的 \(cut(idx)\) 将所有行按分割出的左边矩阵每行的 \((Mn,Mx)\) 按 \(Mn\) 排序。
-
枚举后缀 \(O(1)\) check 方案合法性。
如果我们可以在 \(O(1)\) 的时间内 check 方案的合法性,那么就可以在 \(O(nm\log n)\) 的时间内解决这个问题。
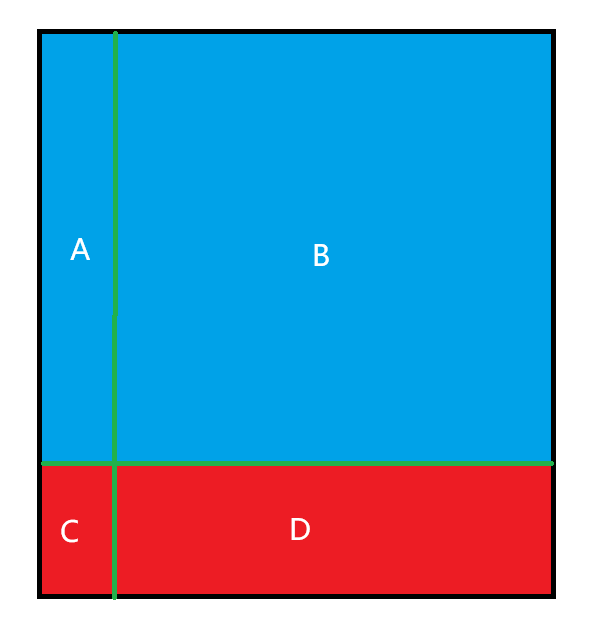
我们发现,实质上在将所有行排列后,相当于枚举两条直线将矩阵分成四个部分,我们的限制为 \(\min(C) > \max(A),\min(B) > \max(D)\) ,在枚举的过程维护前缀 \(\min,\max\) 即可。
我们考虑上述做法正确的根本性原因。
一个很重要的转化是,我们用每一行的前缀 \(\min\) 代表出每行的相对关系,即选了 xx 行,一定选 yy 行。
但实际上,回归题目限制,我们从每一行的前缀中随便选一个代表元素 \(d_i\) ,如果我们选了第 \(k\) 行,那么所有 \(d_i\ge d_k\) 的行 \(i\) 也一定必选。
因为每个前缀都包含第一列的元素,因此我们可以只按第一列元素排序一次,可以做到 \(O(n\log n + nm)\) 的复杂度。


