Slope Trick & 数据结构维护分段函数学习笔记

基础理论

一个函数被称为 slope-trick-able function 当且仅当满足于：

• 其是连续的。

• 可以被分成多个部分，其中每个部分是一个线性函数。

• 是一个凸/凹函数 ： 当从左向右扫描函数时，每个部分的斜率是不减小或不增大的。

例如，函数 \(f(x)=|x|\) 就是一个 slope-trick-able function 。

因为它可以被分成两个部分，且每个部分是一个线性函数：\(y=-x,x\in (-\infty,0)\) 于与 \(y=x,x\in[0,\infty)\) 。

定义 slope changing point 为点 \(x_{change}\) 当且仅当点 \(x_{change}\) 左边直线的斜率与点 \(x_{change}\) 右边直线的斜率不同。

例如对于函数 \(f(x)=|x|\) ，点 \(x=0\) 就是一个 slope changing point 。

但对于一个 slope-trick-able function 可能有多个 slope changing point 。

接下来来看这样一个函数：

\[y=g(x)= \begin{cases} 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x< 2 \\ x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2 \le x < 8 \\4x-24 \ \ \ \ \ \ \ x\ge 8 \end{cases} \]

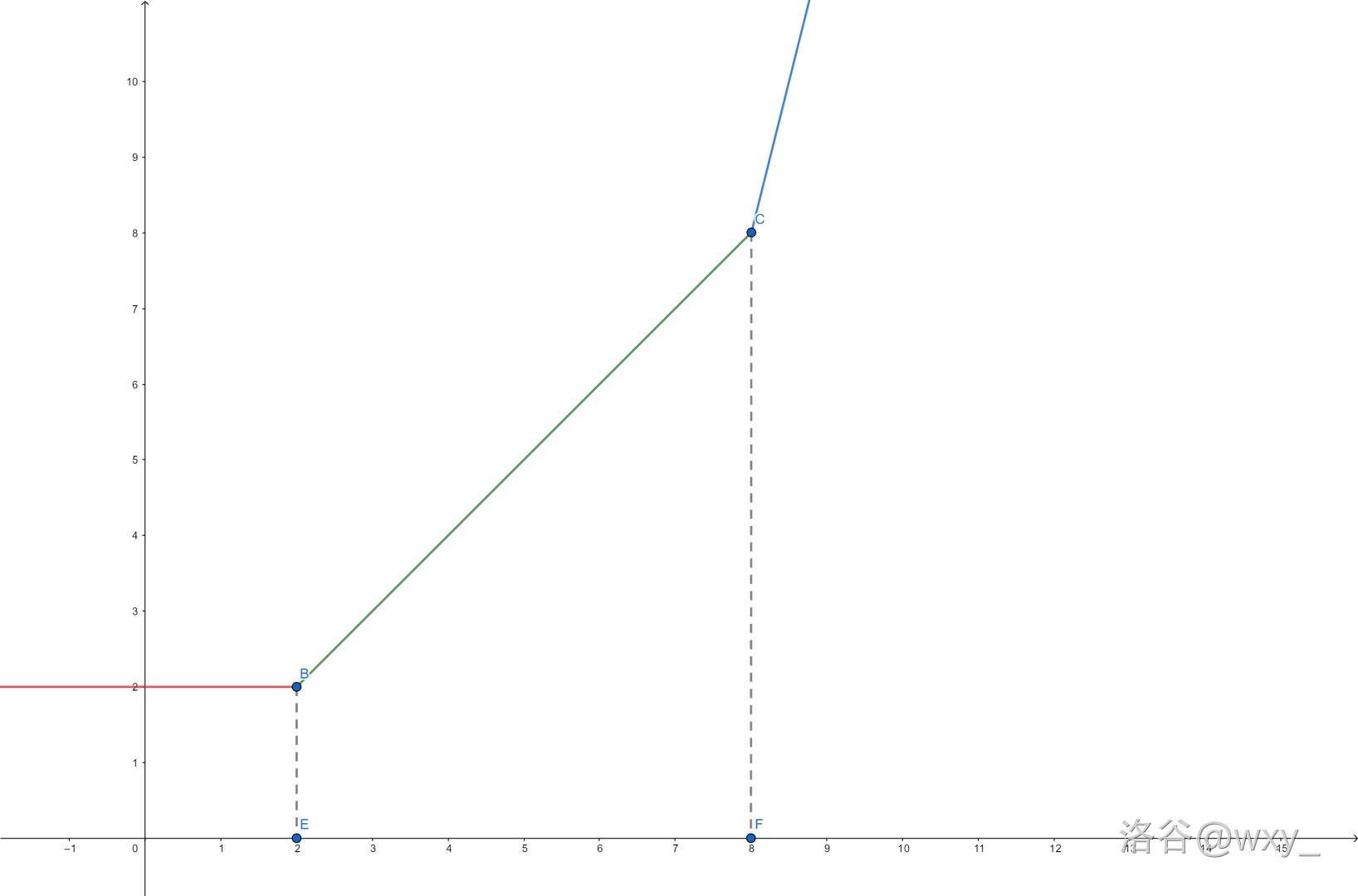
\(x=2\) 和 \(x=8\) 就是 \(g(x)\) 的两个 slope changing point 。

用一种简单的形式表示 convex slope-trick-able function ：

用最左端或最右端的线性函数与由多个 slope changing point 组成的多重集来表示一个 slope-trick-able function ，其中多重集每个元素的个数代表斜率在该点变化的值。

例如 \(f(x)=|x|\) 可以如下表示 ： \([y=-x,S=\{0,0\}]\) 。

\(g(x)\) ，可以如下表示：\([y=4x-24,S=\{2,8,8,8\}]\) 。

并且，通过存储这些值我们可以通过待定系数法重构函数的每个部分从而构建函数。

定理. 若 \(g(x)\) 与 \(f(x)\) 均为 slope-trick-able function 且均为凹的或均为凸的，那么 \(h(x)=g(x)+f(x)\) 也为 slope-trick-able function ，且 \(S_h=S_g\bigcup S_f\)。

Slope Trick 的应用

CF713C

给定一个有 \(n\) 个正整数的数组，一次操作中，可以把任意一个元素加一或者减一。（元素可以被减至负数或 \(0\)），求使得原序列严格递增的最小操作次数。

一个平凡的转化即： \(b[i]=a[i]-i\) ，求 \(b[i]\) 通过操作变成非严格递增的最小操作次数。

令 \(f_i(x)\) 为考虑前 \(i\) 个位置 \(b[i]\le x\) 通过操作变成非严格递增的最小操作次数，\(g_i(x)\) 为考虑前 \(i\) 个位置 \(b[i]= x\) 通过操作变成非严格递增的最小操作次数。

我们发现， \(f_0(x)=0\) ，因此可以将 \(f_0(x)\) 看成 slope-trick-able function 。

若 \(f_{i-1}(x)\) 为 slope-trick-able function ，那么 \(g_i(x)=f_{i-1}(x)+|b[i]-x|\) 也为 slope-trick-able function 。

接下来考虑 \(f_i(x)=\min(g_i(t),t\le x)\) 的性质。

我们发现，对一个凸函数前缀取 \(\min\) 相当于将后缀的一段拉平，其一定也是凸函数。

因此 \(f_i(x)\) 一定是凸函数。

并且可以通过归纳法证明，\(g_i(x)\) 的最右段的斜率一定是 \(1\) ，因此可以直接用 priority_queue 维护 \(f_i(x)\) 和 \(g_i(x)\) 的 slope changing point 集合，同时维护最右端直线的解析式，复杂度 \(O(n\log n)\) 。

#include <bits/stdc++.h>

#define rep(i,l,r) for (int i = l; i <= r; i++)
#define per(i,r,l) for (int i = r; i >= l; i--)
#define fi first
#define se second
#define prt std::cout
#define gin std::cin
#define edl std::endl
#define int long long

namespace wxy{

const int N = 3010;

int a[N],b[N],n;

struct line{int k,b;};

inline line add(line a,line b){
    line res; res.k = a.k + b.k;
    res.b  = a.b + b.b;
    return res;
}

inline int get(line a,int x){
    return x * a.k + a.b;
}

std::priority_queue<int> q;

inline void main(){
    #ifndef ONLINE_JUDGE
        freopen("in.in","r",stdin);
        freopen("out.out","w",stdout);
    #endif
    gin >> n;
    rep(i,1,n) gin >> a[i];
    rep(i,1,n) b[i] = a[i] - i;
    line st; st.k = st.b = 0; int ans = 0;
    rep(i,1,n){
        line newline;
        newline.k = 1; newline.b = -1 * b[i];
        st = add(st,newline);
        q.push(b[i]); q.push(b[i]);
        int x = q.top(); q.pop(); 
        ans = get(st,x);  st.k = 0; st.b = ans;
    }
    prt << ans;
}

}signed main(){wxy::main(); return 0;}