网络流之最大流
什么是网络流:
网络流就是给出一个图,然后每条边上有一个最大的流量(容量),只有出流没有入流的点叫做源点,只有入流没有出流的点叫做汇点。
残余网络:
不断地给每条边分配流量,然后用其剩余的容量减去这些流量,得到残量,残量构成残余网络。
增广路:
在残余网络中,还可以继续分配流量的路径(该路径上每条流的残量都不为0)叫做增广路。
依据以上定义,可以得出三条性质:
(1) 每条流的流量一定小于容量
(2)每个点的入流与出流相等
(3)从u到v的流量=从v到u的流量的相反数
网络流最大流
最大流算法就是指求一种流量方案,使得从源点到汇点的流量最大
求解:
每次去dfs找增广路,然后将增广路上每条流都减去最小的那条流的残量,也就是将该增广路上的一条流的残量变为0,直到找不到增广路为止。
但是发现这样是有问题的,
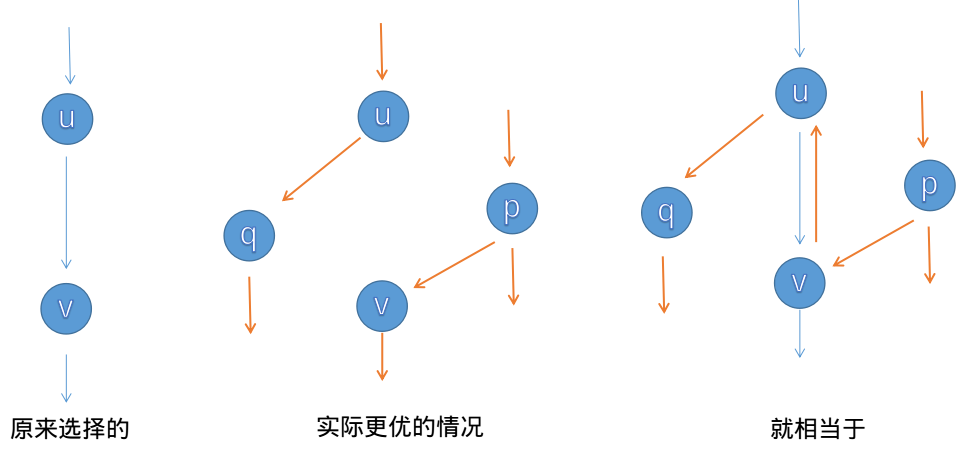
比如上面这种情况,本来增广路选择的是从u->v,但是可以找到两个点q,p达成以上情况,使得流量变大。这时候就要用到反向边,在加边的时候同时加上一条反边,如图3,这样在更新p和q的时候就会走这条反边,然后利用性质3,每将正边减去一个流之后,都将这条反边加上这条流。
Dinic算法:
如果用上面的方法去跑下面的情况
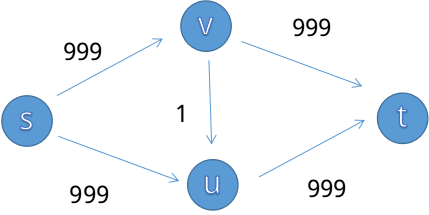
最优的跑法应该是s->v->t但是,程序可能会s->v->u->t,然后就会出现下面的情况

如果有很不慎,程序又跑了s->u->v->t然后就会

这样每次更新1,就要跑999*2次深搜,如果比999更大,就很容易tle,所以就有了Dinic算法
Dinic算法就是在bfs的同时,记录下每个点的深度,比如上面第一次bfs之后各个点的深度:s(0),v(1),u(1),t(2)
然后在dfs的时候,就只去更新深度比自己大1的。这时候上面的例子中,一开始就不会出现s->v->u->t的情况,因为v和u的深度相同。
一道板子题:
代码:

1 #include<cstdio> 2 #include<iostream> 3 #include<queue> 4 #include<cstring> 5 #define change(i) i%2?(i+1):(i-1) 6 using namespace std; 7 const int INF=0x7fffffff; 8 const int N=10010,M=100010; 9 int ejs,n,m,s,t; 10 int head[N],dep[N]; 11 queue<int>q; 12 struct node 13 { 14 int v,w,nxt; 15 }edg[M*2]; 16 void add(int u,int v,int w) 17 { 18 edg[++ejs].v=v; 19 edg[ejs].w=w; 20 edg[ejs].nxt=head[u]; 21 head[u]=ejs; 22 } 23 inline bool bfs() 24 { 25 while(!q.empty()) 26 q.pop(); 27 memset(dep,0,sizeof(dep)); 28 dep[s]=1; 29 q.push(s); 30 while(!q.empty()) 31 { 32 int u=q.front(); 33 q.pop(); 34 for(int i=head[u];i;i=edg[i].nxt) 35 { 36 int v=edg[i].v; 37 if(!dep[v]&&edg[i].w) 38 { 39 dep[v]=dep[u]+1; 40 q.push(v); 41 } 42 } 43 } 44 if(dep[t]) 45 return 1; 46 return 0; 47 } 48 int dfs(int u,int dist) 49 { 50 if(u==t) 51 return dist; 52 for(int i=head[u];i;i=edg[i].nxt) 53 { 54 int v=edg[i].v; 55 if((dep[v]==dep[u]+1)&&edg[i].w) 56 { 57 int di=dfs(v,min(dist,edg[i].w)); 58 if(di>0) 59 { 60 edg[i].w-=di; 61 edg[change(i)].w+=di; 62 return di; 63 } 64 } 65 } 66 return 0; 67 } 68 inline int dinic() 69 { 70 int ans=0; 71 while(bfs()) 72 { 73 int d=0; 74 do 75 { 76 d=dfs(s,INF); 77 ans+=d; 78 }while(d); 79 } 80 return ans; 81 } 82 int main() 83 { 84 scanf("%d%d%d%d",&n,&m,&s,&t); 85 for(int i=1,u,v,w;i<=m;++i) 86 { 87 scanf("%d%d%d",&u,&v,&w); 88 add(u,v,w); 89 add(v,u,0); 90 } 91 printf("%d",dinic()); 92 93 return 0; 94 }
PS :以上内容均参(chao)考(xi)一位大佬的博客



 浙公网安备 33010602011771号
浙公网安备 33010602011771号