【深度学习 - 吴恩达】04 卷积神经网络
本文为吴恩达 Deep Learning 笔记
卷积神经网络基础
计算机视觉
计算机视觉:
Computer Vision 计算机视觉
- 使用传统神经网络解决计算机视觉的问题:
- 神经网络结构复杂,数据量相对不够,容易出现过拟合。
- 所需内存、计算量较大。
- 解决这一问题的方法就是使用卷积神经网络 (CNN)。
边缘检测
边缘检测示例:
Edge Detection 边缘检测
-
在计算机视觉问题中,神经网络由浅层到深层,可以分别检测出图片的边缘特征 、局部特征以及整体特征。
-
最常检测的图片边缘有两类:一是垂直边缘,二是水平边缘。
-
图片的边缘检测可以通过与相应 Filter 进行卷积来实现。
-
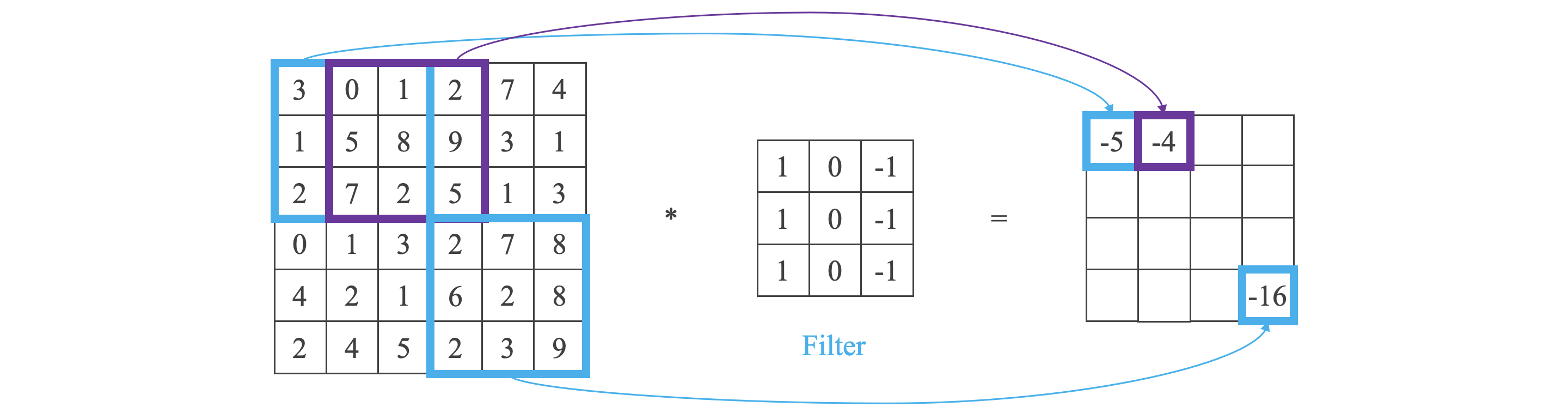
关于卷积运算:
图中,结果的第一行第一列计算方法为:
更多边缘检测内容:
-
图片边缘有两种渐变方式,一种是由明变暗,另一种是由暗变明。实际应用中,这两种渐变方式并不影响边缘检测结果,可以对输出图片取绝对值操作,得到同样的结果。
-
垂直边缘检测和水平边缘检测的 Filter 如下所示:
-
除普通的 Filter 外,还有 Sobel Filter 和 Scharr Filter,他们增加了图片中心区域的权重:
-
在深度学习中,Filter 的数值如标准神经网络中的参数 一样,需要学习得到。
卷积
填充:
Padding 填充
Same Convolutions 卷积前后图片尺寸不变
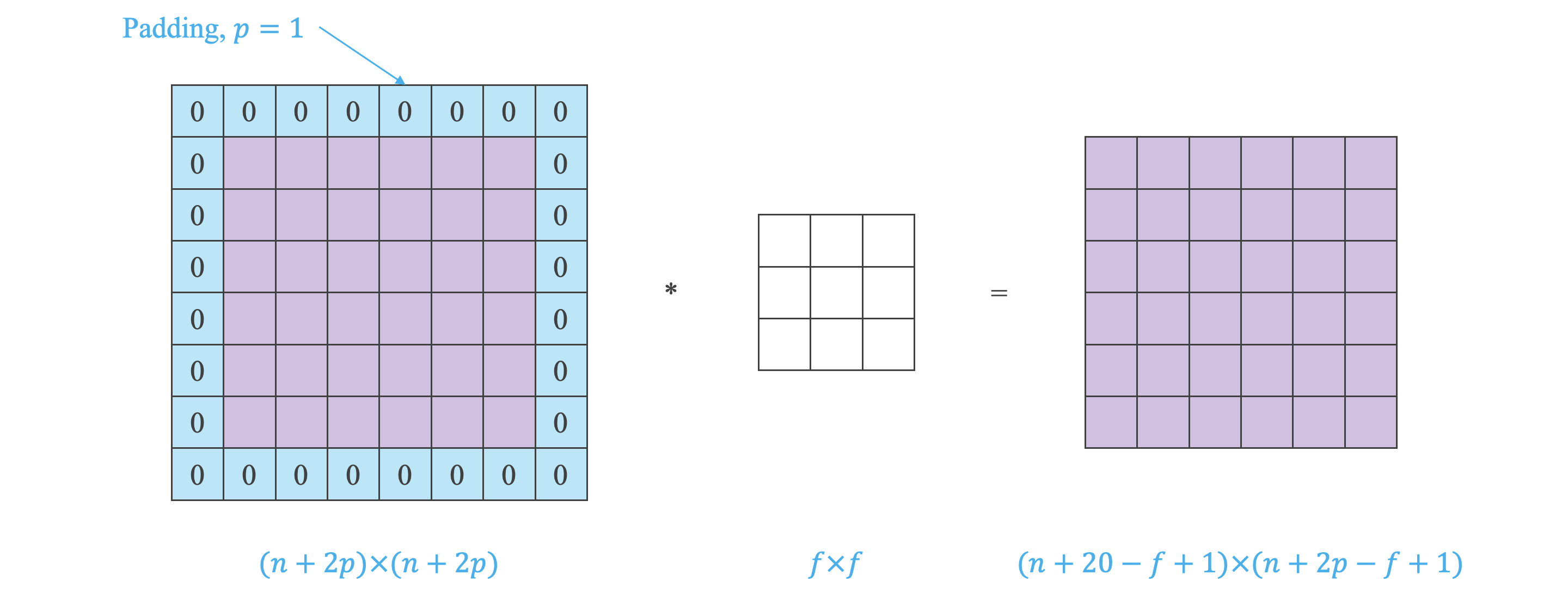
- 卷积会使图片变小,于是我们需要使用 Padding 来扩展原始图片,扩展区域补零。
- 假设原始图片尺寸为 ,Filter 尺寸为 。
- 卷积后图片尺寸为 。
- Padding 长度为 。
- Padding 后原始图片尺寸为 。
- Padding 后再卷积后图片尺寸为 。
- 为保证卷积前后图片尺寸不变,则 ,其中 一般为奇数。
卷积步长:
Strided Convolutions 卷积步长
Cross-correlations 相关系数
-
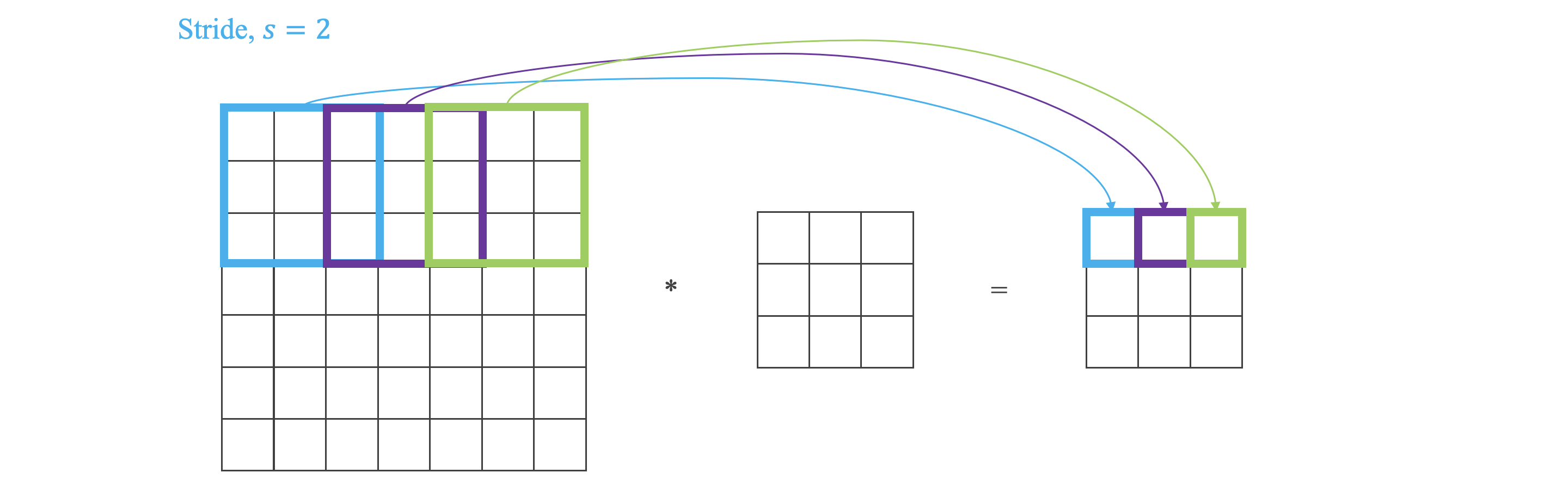
步长 表示 Filter 在原图片中水平方向和垂直方向每次的步进长度。
-
假设原始图片尺寸为 ,Filter 尺寸为 ,Padding 长度为 ,步长为 ,则卷积后图片尺寸为:
-
相关系数与卷积:
- 卷积运算会先将 Filter 绕其中心旋转 ,然后再将旋转后的 Filter 在原始图片上进行滑动计算。
- 相关系数运算过程不会对 Filter 进行旋转,目前为止我们介绍的 CNN 卷积实际上计算的是相关系数,由于 Filter 由学习得到且一般是对称的,所以这不重要。
三维卷积:
- 以上讨论的是灰度图片,只有一个通道,而 RGB 图片有三个通道。
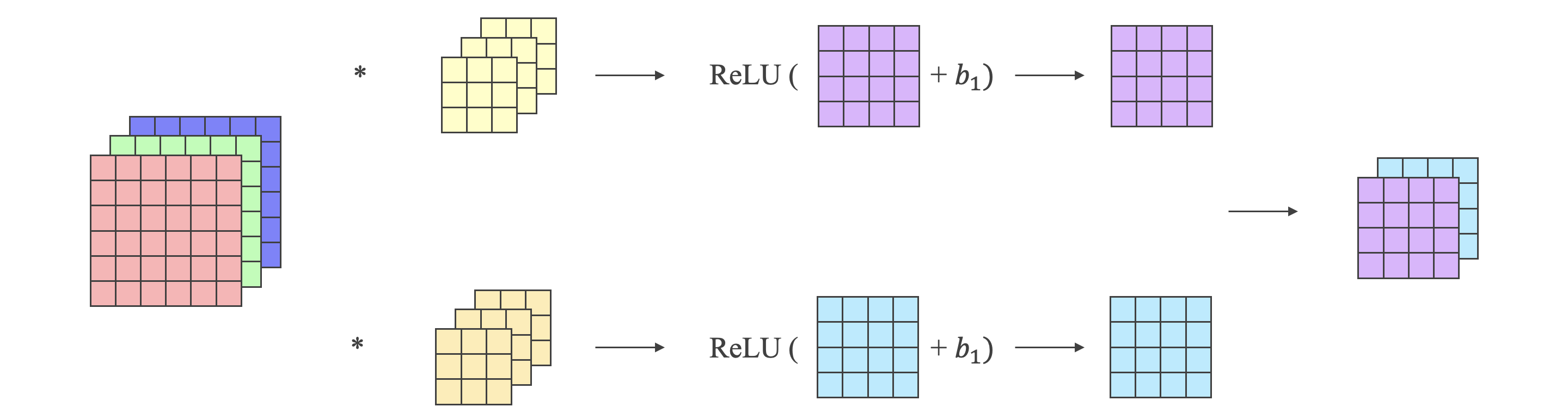
- 三通道图片的卷积运算与单通道图片的卷积运算基本一致:
- 将每个通道与对应的 Filter 进行卷积运算,然后再将三个通道的和相加,得到输出图片的一个像素值。
- 不同通道对应的 Filter 可以不同,如只对 R 通道进行边缘检测,则 G、B 通道的 Filter 将置零。
- 可以设置多个 Filter 组,如第一个 Filter 组实现垂直边缘检测,第二个 Filter 组实现水平边缘检测。
- 假设原始图片尺寸为 ,Filter 尺寸为 ,其中 是图片通道数,则卷积后图片尺寸为 ,其中 是 Filter 组个数。
卷积神经网络
单层卷积神经网络:
-
深度神经网络与卷积神经网络:
-
卷积神经网络的符号:
-
: 层的 Filter 维度。
-
: 层的 Padding 长度。
-
: 层的卷积步长。
-
: 层的 Filter 组的数量。
-
输入维度:,其中 和 分别代表图片的长和宽,输入图片不一定是正方形。
-
输出维度:。
-
每个 Filter 组维度为:。
-
的维度:。
-
的维度:。
-
简单卷积网络示例:
-
CNN 模型示例:
-
随着 CNN 层数增加, 和 一般逐渐减小, 一般逐渐增大。
-
CNN 有三种类型的层:卷积层、池化层、全连接层。
池化层:
Pooling 池化
- 池化层用来减小尺寸,减少噪声影响。
- 池化层没有卷积运算,与卷积层相比,Filter 没有参数 ,有参数 和 。
- Max Pooling 在 Filter 滑动区域内取最大值;Average Pooling 在 Filter 滑动区域内取平均值。
卷积神经网络示例:
为什么要使用卷积:
- 使用卷积可以减少参数。
经典 CNN 网络实例详解
经典网络
为什么要进行实例研究:
- 经典 CNN 网络有:LeNet-5、AlexNet、VGG、ResNet、Inception Neural Network。
经典网络:
-
LeNet-5:
-
LeNet-5 是第一个成功应用于数字识别问题的卷积神经网络。
-
典型的 LeNet-5 结构包含 CONV layer,POOL layer 和 FC layer,顺序一般是:
-
在 LeNet-5 提出时激活函数是 Sigmoid 和 tanh,池化层是 Average Pool,现在根据需要,可以使用 ReLU 和 Max Pool。
-
-
AlexNet:
- AlexNet 与 LeNet-5 类似,但是更复杂,LeNet-5 大约有六万个参数,AlexNet 大约有六千万个参数。
- AlexNet 与 LeNet-5 类似,但是更复杂,LeNet-5 大约有六万个参数,AlexNet 大约有六千万个参数。
-
VGG:
-
增加网络的深度能够在一定程度上影响网络最终的性能。
-
VGG-16 在每一组卷积层进行翻倍操作。
-
残差网络
ResNet:
Residual Networks 残差网络
Residual Block 残差块
Plain Networks 非残差网络
-
随着神经网络层数变多和网络变深,会带来严重的梯度消失和梯度爆炸问题,残差网络是一种解决方法。
- 残差网络人为地让神经网络某些层跳过下一层神经元的连接,隔层相连,弱化每层之间的强联系。
- 这种模型结构对于训练非常深的神经网络效果很好。
-
公式:
残差网络为什么有用:
- 通过残差网络:
- 当发生梯度消失 () 时,能建立 与 的线性关系。
- 当没有发生梯度消失时,残差块会忽略 Short Cut,得到与没有使用残差网络时同样效果的非线性关系。
- 如果残差块中 和 维度不同,可以引入矩阵 ,使 与 维度相同:
- 可以将 作为参数学习。
- 也可以使 仅起到给 截断或补零的作用。
Inception
卷积:
- 卷积:Filter 的维度为 ,即卷积操作等同于乘积操作。
- 池化可以减小 和 , 卷积可以减小通道数 。
Inception 网络简介:
Bottleneck Layer 瓶颈层
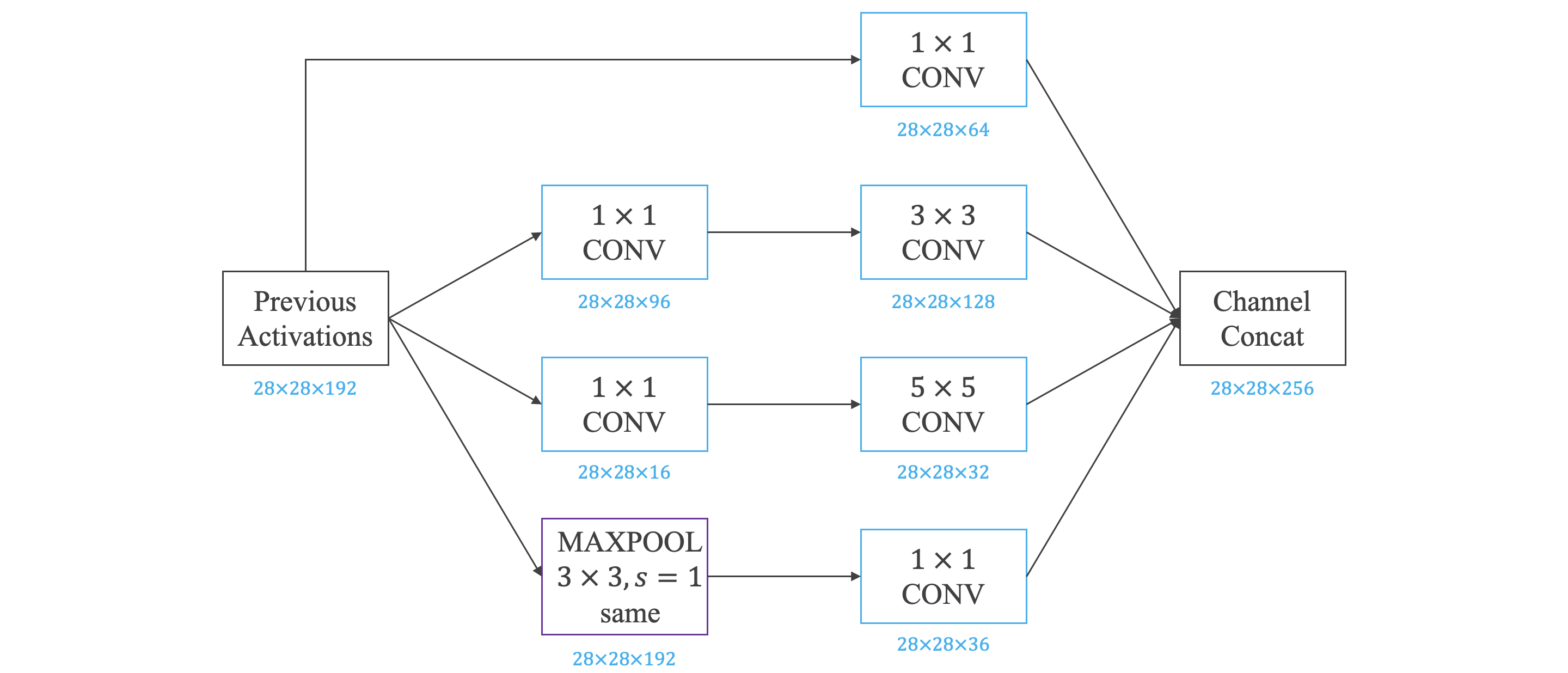
- 在之前介绍的 CNN 中,单层的 Filter 尺寸是固定的,在 Inception 网络中,单层网络上可以使用不同尺寸的 Filter 进行 Same Convolutions,然后将各 Filter 得到的结果拼接。此外,还可以将卷积层与池化层混合。
- Inception 网络的计算量很大,我们可以通过 卷积来减少计算量, 卷积层将通道数减少,又被称为瓶颈层。
Inception 网络:
- 网络中间隐藏层也可以作为输出层 Softmax,有利于防止发生过拟合。
其他
使用开源的实现方案:
- 略。
迁移学习:
- 参考《迁移学习》一节。
- 越多的数据意味着冻结越少的层,训练更多的层。
数据扩充:
Color Shifting 色调转换
- 参考《其他正则化方法》一节。
- 当数据不够时,使用数据扩充 (Data Augmentation) 以获得更多样本,如镜像翻转、随机裁剪、色彩转换等。
计算机视觉现状:
Hand-engineering 手工工程
Ensembling 集成
Multi-crop At Test Time 测试阶段数据扩增
- 当数据量较少时,常常需要手工工程。
- 在模型研究或者竞赛方面,有一些方法能够有助于提升神经网络模型的性能:
- 集成:独立地训练几个神经网络,并平均输出它们的输出。
- 测试阶段数据扩增:将数据扩增应用到测试集,对结果进行平均。
目标检测
目标定位与特征点检测
目标定位:
Object Detection 目标检测
Object Localization 目标定位
-
目标定位不仅要求判断出图片中物体的种类,还要在图片中标记出它的具体位置。
-
目标定位和目标检测:
- 目标定位,只有一个较大的对象位于图片中间位置。
- 目标检测,图片可以含有多个对象,甚至单张图片中会有多个不同分类的对象。
-
对于标准的 CNN 分类模型,可以输出一个 向量,每个元素的值分别对应 Pedestrain, Car, Motorcycle, Background 四类。
-
对于目标定位模型,将输出 向量,除 个分类标签 (Pedestrain, Car, Motorcycle) 外,还有:
- 表示矩形区域是目标的概率,若 ,则是没有检测到目标,其他参数均可忽略。
- 和 表示目标中心位置坐标,设定图片左上角是 ,右下角是 。
- 和 表示矩形区域的宽和高。
-
损失函数:
-
若 :
-
若 :
-
特征点检测:
Landmark Detection 特征点检测
- 特征点检测:对目标的关键特征点坐标进行定位,而非使用矩形区域检测目标位置。例:人脸识别、人体姿势动作。
- 如果有 个特征点,则输出的向量中有 个值,包括每个特征点的坐标和一个标志为用来判断是否是目标。
滑动窗算法
目标检测:
Sliding Windows Detection 滑动窗算法
- 目标检测的一种简单方法是滑动窗算法:
- 在训练样本集上搜集相应的各种目标图片和非目标图片,图片尺寸较小,尽量仅包含相应目标。
- 使用这些训练集构建 CNN 模型。
- 在测试图片上,选择大小适宜的窗口、合适的步进长度,进行从左到右、从上倒下的滑动。
- 每个窗口区域都送入之前构建好的 CNN 模型进行识别判断。
- 滑动窗算法的优缺点:
- 原理简单,不需要人为选定目标区域。
- 滑动窗的大小和步进长度都需要人为直观设定:
- 滑动窗过小或过大,步进长度过大,均会降低目标检测正确率。
- 滑动窗和步进长度较小,整个目标检测的算法运行时间会很长。
基于卷积的滑动窗口实现:
-
之前的滑动窗算法需要反复进行 CNN 正向计算,而利用卷积操作,则不管原始图片有多大,只需要进行一次 CNN 正向计算。
-
首先需要对 CNN 网络结构做一些调整,以便对进入网络的单个滑动窗口区域更快捷计算:
- 具体做法是把全连接层转变成为卷积层。
- 将全连接层转变成为卷积层的方法是,使用与上层尺寸一致的 Filter 进行卷积运算,如:
- 。
- 。
-
假设滑动窗口的大小是 ,测试集图片的大小是 。
-
单个滑动窗口的 CNN 网络为:
-
将测试集图片通过同样的 CNN 网络,最后会得到 的输出,其中 代表一共有 个窗口结果:
-
-
窗口步进长度与选择的 Max Pool 大小有关,如果需要步进长度为 ,只需设置 Max Pool 为 即可。
YOLO
Bounding Box 预测:
- 滑动窗口算法有时会出现滑动窗不能完全涵盖目标的问题,YOLO 算法可以解决这类问题。
- YOLO 算法流程:
- 首先将原始图片分割成 网格,每个网格代表一块区域。
- 对原始图片构建 CNN 网络,输出层为 ,其中 为 《目标定位》一节提到的 个值。
- 如果中心坐标 不在当前网格中,则 。
- 网格左上角为 ,右下角为 , 和 的值在 和 之间, 和 的值可以大于 。
交并比:
Intersection Over Union 交并比 (IoU)
-
IoU 用于评价目标检测算法的准确性。
-
真实目标区域与检测目标区域的交集为 ,并集为 。
-
IoU 的值在 和 之间,越接近 代表两块区域越接近。
非最大值抑制:
Non-max Suppression 非最大值抑制 (NMS)
- YOLO 算法中,可能会出现多个网格都检测出到同一目标的情况,即几个相邻网格都判断出同一目标的中心坐标在其内。
- 可以使用非最大值抑制判断哪个网格最为准确。
- 非最大值抑制算法流程:
- 剔除 值小于某阈值的所有网格。
- 选取 值最大的网格,利用 IoU,摒弃与该网格交叠较大的网格。
- 对剩下的网格,重复上一步。
- 上面提到的步骤适用于单类别目标检测,如果要进行多个类别目标检测,对于每个类别,应该单独做一次非极大值抑制。
Anchor Boxes:
- 那对于多个目标重叠的情况,如一个人站在一辆车前面,需要使用不同形状的 Anchor Boxes 来检测。
- 例,如果同一网格出现了两个目标——人和车:
- 我们可以设置 Anchor Box1 检测人,Anchor Box2 检测车。
- 如果原来的输出维度是 ,则使用 Anchor Boxes 后输出维度为 或 。
- 每个 Anchor Box 都有一个 ,若两个 都大于某一阈值,则检测到两个目标。
- 当同一网格中有两个以上目标或两个目标的 Anchor Box 高度重合时,算法效果不好。
- Anchor Box 可以通过 K-means 聚类,选择一组有代表性的 Anchor Box。
YOLO:
- 算法流程:
- 对每个网格,预测得到 Bunding Box。
- 剔除掉概率低的预测结果。
- 对每个类别应用非极大值抑制得到最终结果:
- 最终结果的维度是 。
- 指图片分割成 网格。
- 指 个 Anchor Boxes。
- 指 、、、、 和 Pedestrain, Car, Motorcycle 三种类别。
R-CNN
候选区域:
Region CNN 带区域的 CNN
Region Proposal 候选区域
- 滑动窗口目标检测算法对一些明显没有目标的区域也进行了扫描,这降低了算法的运行效率。
- R-CNN 对输入图片运行图像分割算法,在不同的色块上找出候选区域,只在这些区域运行分类器。
- R-CNN 运行速度慢,有一系列改进:Fast R-CNN、Faster R-CNN。但是大多数情况仍比 YOLO 慢。
- YOLO 系列的算法叫做 1-stage 目标检测方法;RCNN 系列的算法也叫做 2-stage 目标检测算法,因为会先产出后候选框,再预测和调整。
人脸识别与神经风格迁移
人脸识别
人脸识别:
Face Verification 人脸验证
Face Recognition 人脸识别
- 人脸验证:输入的人脸是否与某个已知的身份信息对应。
- 人脸识别:输入的人脸是否与已知的多个身份信息中的某一个对应。
One-Shot 学习:
Similarity Function 相似函数
- One-Shot 学习:
- 每个人的训练样本只包含一张照片,然后训练一个 CNN 模型来进行人脸识别。
- 若一共有 个人,则输出 Softmax 是 维。
- One-Shot 的缺点:
- 训练样本少,CNN 不够健壮。
- 如果增加一个人,需要重新构建 CNN 网络。
- 相似函数:
- 为解决 One-Shot 的缺点,先介绍这一概念。
- 相似函数表示两张图片的不同的程度 (degree of difference between images) ,用 来表示。 越小,两张图片越相似。
- 在人脸识别问题中,会计算输入图片与数据库中 个目标图片的相似函数,取其中 最小的目标为匹配对象。若所有的 都很大,则表示数据库没有这个人。
Siamese 网络:
Siamese 孪生网络
- Siamese:让图片经过 CNN 网络得到全连接层 ,将全连接层 看作原始图片的编码,表征原始图片的关键特征。
- 相似函数可以表示为:。
- 不同图片所通过的 CNN 网络是相同的,我们的目标是通过梯度下降求出网络的参数。
Triplet 损失:
-
Triplet 损失需要每个样本包含三张图片:靶目标 (Anchor)、正例 (Positive)、反例 (Negative)。
-
我们希望靶目标与正例的相似函数尽可能小,靶目标与反例的相似函数尽可能大,前者远小于后者:
-
可定义损失函数和代价函数,其中 为超参数:
-
损失函数:
-
代价函数:
-
人脸验证与二分类:
-
除构造 Triplet 损失来解决人脸识别问题之外,还可以使用二分类结构。
-
输出表达式:
或:
-
一种减少计算量的方法:
- 训练好模型后,将数据库中每张图片的编码层 保存。
- 使用时,只需计算输测试入图片的 Siamese 网络,即 。
神经风格迁移
什么是神经风格迁移:
Neural Style Transfer 神经风格迁移
- 将一张图片的风格 "迁移" 到另外一张图片中,C 表示内容图片,S 表示风格图片,G 表示生成的图片。
深度卷积神经网络学到了什么:
- 略。
代价函数:
-
G的代价函数由两部分组成:C 与 G 的相似程度和 S 与 G 的相似程度。
-
神经风格迁移的基本算法流程是:首先令 G 为随机像素点,然后使用梯度下降算法,不断修正 G 的所有像素点,使得代价函数不断减小。
内容代价函数:
Content Cost Function 内容代价函数
-
CNN 的每个隐藏层分别提取原始图片的不同深度特征,由简单到复杂。
-
风格迁移时使用的隐藏层不能太深也不能太浅,如果太浅,G 与 C 会非常接近,如果太深,G 中会出现 C 中的物体。
-
内容代价函数,其中 是网络中间层激活函数的输出:
风格代价函数:
Style Cost Function 风格代价函数
Style Matrix 风格矩阵
-
图片的风格可以定义成 CNN 网络中第 隐藏层不同通道间激活函数的相关系数。
-
对于风格图像 S,选定网络中的第 层,定义图片的风格矩阵为:
其中, 和 分别为第 层的高和宽, 和 为选定的通道。同理,对于生成图像 G,有风格矩阵 。
-
风格代价函数,其中 为超参数:
推广至一维和三维:
- 对于一维数据,例:
- 输入维度 ,Filter 维度 ,Filter 组数 。
- 输出维度 。
- 对于三维数据,例:
- 输入维度 ,Filter 维度 ,Filter 组数 。
- 输出维度 。



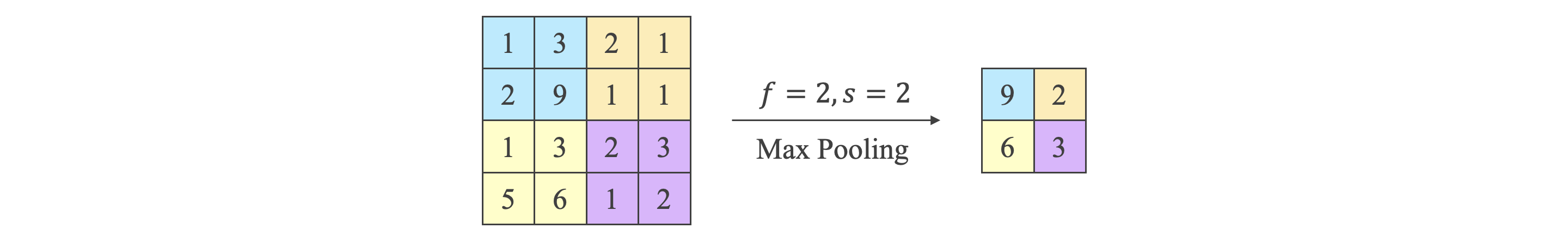




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!