【Deep Learning】02 优化深度神经网络

本文为吴恩达 Deep Learning 笔记

深度学习的实用层面

概念

训练 / 验证 / 测试：

Training Set 训练集

Development Set 验证集

Test Set 测试集

偏差 / 方差：

Bias 偏差

Variance 方差

Underfitting 欠拟合

Overfitting 过拟合

Optimal Error / Bayes Error 理想误差 / 贝叶斯误差

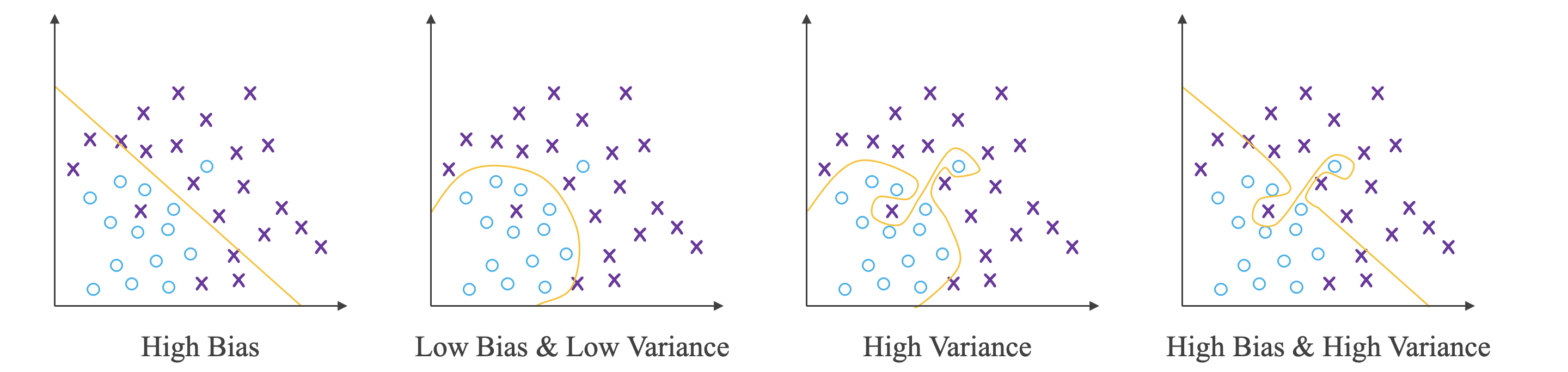
• 对于猫的识别，假设理想误差为 \(0\%\)，则：

  	High Bias	Low Bias & Low Variance	High Variance	High Bias & High Variance
  训练集误差	\(15\%\)	\(0.5\%\)	\(1\%\)	\(15\%\)
  测试集误差	\(16\%\)	\(1\%\)	\(11\%\)	\(30\%\)

机器学习的基本方法：

• 高方差 (High Variance)：过拟合，增加训练样本数据，进行正则化，选择其他更复杂的神经网络模型。
• 高偏差 (High Bias)：欠拟合，增加神经网络的隐藏层个数、神经元个数，延长训练时间，选择其它更复杂的神经网络模型。

正则化

正则化：

Regularization 正则化

L1 Regularization L1 正则化

L2 Regularization L2 正则化

Regularization Parameter 正则化参数

Frobenius Norm Frobenius 范数

Weight Decay 权重下降

• 对于逻辑回归：

  • L2 正则化：

    \[J(w, b) = \frac{1}{m} \sum_{i = 1}^{m} L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \left \| w \right \|_2^2 ,\quad \left \| w \right \|_2^2 = \sum_{j = 1}^{n_x}w_j^2 = w^\mathrm{T}w \]

  • L1 正则化：

    \[J(w, b) = \frac{1}{m} \sum_{i = 1}^{m} L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \left \| w \right \|_1 ,\quad \left \| w \right \|_1 = \sum_{j = 1}^{n_x}\left | w_j \right | \]

  • 其中 \(\lambda\) 是超参数。

  • 与 L2 正则化相比，L1 正则化得到的 \(w\) 更加稀疏，即很多 \(w\) 为零值，节约存储空间。

  • 然而，L1 正则化在解决高方差 (High Variance) 方面比 L2 正则化并不更具优势。而且 L1 的在微分求导方面比较复杂，所以一般 L2 更加常用。

• 对于深层神经网络：

  \[J(w^{[1]}, b^{[1]}, \cdots , w^{[L]}, b^{[L]}) = \frac{1}{m} \sum_{i = 1}^{m} L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \sum_{l=1}^L \left \| w^{[l]}\right \|_F^2 ,\quad \left \| w^{[l]} \right \|_F^2 = \sum_{i = 1}^{n^{[l]}} \sum_{j = 1}^{n^{[l-1]}}(w_{ij}^{[l]})^2 \]
  • 其中 \(\left \| w^{[l]} \right \|_F\) 是 Frobenius 范数。

• 由于加入了正则化项，梯度下降算法中的 \(dw^{[l]}\) 计算表达式需要做如下修改：

  \[dw^{[l]} = dw^{[l]}_{before} + \frac{\lambda}{m}w^{[l]} \\ w^{[l]} := w^{[l]} − \alpha \cdot dw^{[l]} = (1 - \alpha \frac{\lambda}{m})w^{[l]} - \alpha \cdot dw_{before}^{[l]} \]

丢弃法正则化：

Dropout Regularization 丢弃法

Inverted Dropout Technique 反向随机失活技术

• 丢弃法是指在深度学习网络的训练过程中，对于每层的神经元，按照一定的概率将其暂时从网络中丢弃。也就是说，每次训练时，每一层都有部分神经元不工作，起到简化复杂网络模型的效果，从而避免发生过拟合。

dl = np.random.rand(al.shape[0], al.shape[1]) < keep_prob  # keep_prob 是要保留的神经元比例
al = np.multiply(al, dl)
al /= keep_prob  # 使下一层神经元的输入值尽量保持不变

• 对于 \(m\) 个样本，单次迭代训练时，随机删除掉隐藏层一定数量的神经元，在删除后的剩下的神经元上正向和反向更新权重 \(w\) 和常数项 \(b\)。
• 下一次迭代中，再恢复之前删除的神经元，重新随机删除一定数量的神经元，进行正向和反向更新 \(w\) 和 \(b\)，不断重复上述过程，直至迭代训练完成。
• 训练结束后，在测试和实际应用模型时，不需要进行随机删减神经元，所有的神经元都在工作。

理解丢弃法：

• 不同隐藏层的系数 keep_prob 可以不同。
• 神经元越多的隐藏层，keep_prob 可以设置得小一些；神经元越少的隐藏层，keep_prob 可以设置的大一些。

其他正则化方法：

Data Augmentation 数据扩充

Early Stopping 早停法

• 数据增强：对已有的图片进行水平翻转、垂直翻转、任意角度旋转、缩放或扩大等。
• 早停法：一个神经网络模型随着迭代训练次数增加，训练集代价一般是单调减小的，而测试集代价先减后增。训练次数过多时，模型会对训练样本拟合的越来越好，但是对验证集拟合效果逐渐变差，即发生了过拟合。因此，可以通过训练集代价和测试集代价随着迭代次数的变化趋势，选择合适的迭代次数。

输入

标准化输入：

Normalizing 标准化

• 标准化：将原始数据减去其均值 \(\mu\) ，再除以方差 \(\sigma^2\)

  \[\mu = \frac{1}{m} \sum_{i = 1}^m X^{(i)} ,\quad \sigma^2 = \frac{1}{m} \sum_{i = 1}^m (X^{(i)})^2 ,\quad X := \frac{X −\mu}{\sigma^2} \]

• 训练集和测试集都要进行标准化操作。

梯度

梯度消失和梯度爆炸：

Vanishing Gradients 梯度消失

Exploding Gradients 梯度爆炸

• 当训练一个层数非常多的神经网络时，计算得到的梯度可能非常小或非常大。

神经网络的权重初始化：

• 这是改善梯度消失和梯度爆炸的一种方法。

• 如果激活函数是 \(tanh\)：

  w[l] = np.random.randn(n[l], n[l-1]) * np.sqrt(1 / n[l-1])
  

• 如果激活函数是 \(ReLU\)：

  w[l] = np.random.randn(n[l], n[l-1]) * np.sqrt(2 / n[l-1]) 
  

• 其他初始化方法：

  w[l] = np.random.randn(n[l], n[l-1]) * np.sqrt(2 / n[l-1] * n[l]) 
  

梯度的数值逼近：

• 函数 \(g\) 在 \(\theta\) 点的梯度可以表示为：
  \[g(\theta) = \frac{f(\theta + \varepsilon) - f(\theta - \varepsilon)}{2\varepsilon} \]

梯度检验：

• 将代价函数 \(J(W^{[1]}, b^{[1]}, \cdots, W^{[L]}, b^{[L]})\) 表示为 \(J(\theta)\)。

  • 由 \(J(\theta)\) 计算 \(d\theta_i\)：

    \[d\theta_i = \frac{J(\theta_1, \theta_2, \cdots, \theta_i + \varepsilon, \cdots) - J(\theta_1, \theta_2, \cdots, \theta_i - \varepsilon, \cdots)}{2\varepsilon} \]

  • 由 \(d\theta_i\) 得 \(d\theta_{approx}\)。

• 由反向传播 \(dW^{[1]}, db^{[1]}, \cdots, dW^{[L]}, db^{[L]}\) 得到 \(d\theta\)。

• 计算 \(d\theta_{approx}\) 和 \(d\theta\) 的欧式距离比较二者相似度。

  \[\frac{\left \| d\theta_{approx} - d\theta \right \|_2}{\left \| d\theta_{approx} \right \|_2 + \left \| d\theta \right \|_2} \]

关于梯度检验的注记：

• 不要在整个训练过程中都进行梯度检查，仅仅作为 debug 使用。
• 如果梯度检查出现错误，找到对应出错的梯度，检查其推导是否出现错误。
• 注意不要忽略正则化项，计算近似梯度的时候要包括进去。
• 梯度检查时关闭 Dropout，检查完毕后再打开 Dropout。
• 随机初始化时运行梯度检查，经过一些训练后再进行梯度检查（不常用）。

优化算法

Mini-batch

Mini-batch 梯度下降：

Batch Gradient Descent 批梯度下降法

Mini-batch Gradient Descent Mini-batch 梯度下降法

• 如果样本数量 \(m\) 很大，例如达到百万数量级，训练速度往往会很慢，因为每次迭代都要对所有样本进行进行求和运算和矩阵运算。

• 我们可以把 \(m\) 个训练样本分成若干个子集，称为 Mini-batches，这样每个子集包含的数据量就小了，然后每次在单一子集上进行神经网络训练，速度就会大大提高。这种梯度下降算法叫做 Mini-batch 梯度下降法。

• 符号 \(X^{\{t\}}\), \(Y^{\{t\}}\)：第 \(t\) 组 Mini-batch。

• 流程：

  for t in range(T):
      Forward Propagation
      Compute Cost Function
      Backward Propagation
      W := W − alpha * dW
      b := b − alpha * db
  

  • 对于 Mini-batch 梯度下降法，一个 epoch 会进行 T 次梯度下降。
  • Mini-batch 可以进行多次 epoch，每次迭代，最好将总体训练数据重新打乱、重新分成 T 组。

理解 Mini-batch 梯度下降：

Stochastic Gradient Descent 随机梯度下降

• 使用 Batch Gradient Descent，随着迭代次数增加，代价函数是不断减小的；使用 Mini-batch Gradient Descent，随着在不同的 Mini-batch 上迭代训练，其代价不是单调下降，而是受类似噪音的影响，出现振荡，但整体的趋势是下降的。
• 当 Mini-batch 的大小为 \(m\) 时，即为 Batch Gradient Descent；当 Mini-batch 的大小为 \(1\) 时，即为 Stochastic gradient descent。Mini-batch 的大小推荐设置为 \(64, 128, 256, 512\)。
• Mini-batch 最终会在最小值附近来回波动，难以真正达到最小值处，而且在数值处理上不能使用向量化的方法来提高运算速度。

指数加权平均

指数加权平均：

Exponentially Weighted Averages 指数加权平均

• 公式：
  \[V_t = \beta V_{t-1} + (1-\beta)\theta_t \]
  \(\beta\) 值决定了指数加权平均的天数，近似表示为：
  \[\frac{1}{1 - \beta} \]
  例如 \(\beta=0.9\) 表示将前 \(10\) 天进行指数加权平均。

理解指数加权平均：

v = 0
while (true):
    get next theta
    v := beta * v + (1 - beta) * theta

指数加权平均的参数修正：

• 开始时我们设置 \(V_0 = 0\)，所以初始值会相对小一些，直到后面受前面的影响渐渐变小，趋于正常。

• 可以在每次计算完 \(V_t\) 时，作如下处理：

  \[V_t = \frac{V_t}{1 - \beta^t} \]

其他优化算法

动量梯度下降：

Gradient Descent With Momentum 动量梯度下降

• 在每次训练时，对梯度进行指数加权平均处理，然后用得到的梯度值更新权重 \(w\) 和常数项 \(b\)。

• 公式：

  \[V_{dW} = \beta \cdot V_{dW} + (1 − \beta) \cdot dW ,\quad V_{db} = \beta \cdot V_{db} + (1 − \beta) \cdot db \\ W = W - \alpha V_{dW} ,\quad b = b - \alpha V_{db} \]

• 超参数：\(\alpha\)、\(\beta\)。

RMSprop：

Root Mean Square Prop (RMSprop) 均方根传递

• 公式：

  \[S_W = \beta S_{dW} + (1 − \beta)dW^2 ,\quad S_b = \beta S_{db} + (1 − \beta)db^2 \\ W := W − \alpha \frac{dW}{\sqrt{S_W} + \varepsilon} ,\quad b := b − \alpha \frac{db}{\sqrt{S_b} + \varepsilon} \]

• 为了避免 RMSprop 算法中分母为零，通常可以在分母增加一个极小的常数 \(\varepsilon\)。

Adam 优化算法：

Adaptive Moment Estimation 自适应矩阵估计

• 结合了动量梯度下降算法和 RMSprop 算法。

• 公式：

  \[\begin{aligned} V_{dW} = \beta_1 V_{dW} + (1 − \beta_1)dW &,\quad V_{db} = \beta_1 V_{db} + (1 − \beta_1)db \\ S_{dW} = \beta_2 S_{dW} + (1 − \beta_2)dW^2 &,\quad S_{db} = \beta_2 S_{db} + (1 − \beta_2)db^2 \\ V^{corrected}_{dW} = \frac{V_{dW}}{1 − \beta^t_1} &,\quad V^{corrected}_{db} = \frac{V_{db}}{1 − \beta^t_1} \\ S^{corrected}_{dW} = \frac{S_{dW}}{1 − \beta^t_2} &,\quad S^{corrected}_{db} = \frac{S_{db}}{1 − \beta^t_2} \\ W := W − \alpha \frac{V^{corrected}_{dW}}{\sqrt{S^{corrected}_{dW}} + \varepsilon} &,\quad b := b − \alpha \frac{V^{corrected}_{db}}{\sqrt{S^{corrected}_{db}} + \varepsilon} \end{aligned} \]

• 超参数：\(\alpha\)、\(\beta_1\)、\(\beta_2\)、\(\varepsilon\)。

学习率衰减：

Learning Rate Decay 学习率衰减

• 随着迭代次数增加，令学习因子 \(\alpha\) 逐渐减小。

• 公式：

  \[\alpha = \frac{1}{1 + decay\_rate * epoch}\alpha_0 \quad or \quad \alpha = 0.95^{epoch}\alpha_0 \quad or \quad \alpha = \frac{k}{\sqrt{epoch}}\alpha_0 \quad or \quad \alpha = \frac{k}{\sqrt{t}}\alpha_0 \]
  • \(deacy\_rate\)、\(k\) 是可调参数，\(epoch\) 是训练次数，\(t\) 是 Mini-batch 数量。

局部最优化

局部最优化问题：

Local Optima 局部最优化

Saddle Point 鞍点

Plateau 停滞区

• 大部分梯度为零的 "最优点" 并不是这些凹槽处，而是马鞍状的鞍点 (Saddle Point)。
• 梯度为零并不能保证都是极小值 (Convex)，也有可能是极大值 (Concave)。
• 类似马鞍状的停滞区 (Plateaus) 会降低神经网络学习速度，但是由于随机扰动，梯度一般能够离开鞍点 (Saddle Point)，继续前进，只是在停滞区 (Plateaus) 上花费了太多时间。

总结

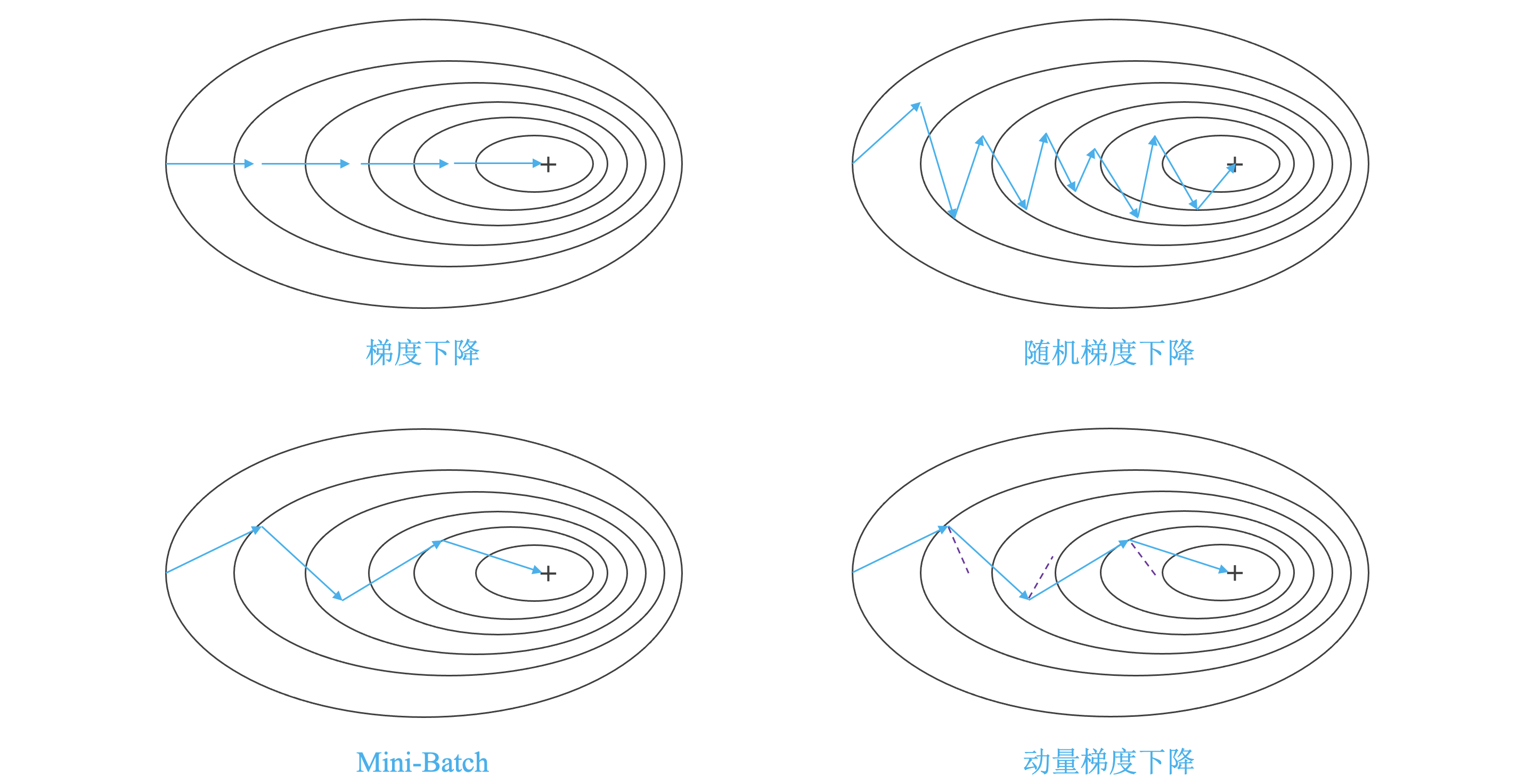
• "+" 表示损失的最小值。

• 梯度下降 (Gradient Descent) 与随机梯度下降 (Stochastic Gradient Descent, SGD)：

  • 梯度下降：

  X = data_input  
  Y = labels  
  parameters = initialize_parameters(layers_dims)  
  for i in range(0, num_iterations):  
      a, caches = forward_propagation(X, parameters)  
      cost = compute_cost(a, Y)  
      grads = backward_propagation(a, caches, parameters)  
      parameters = update_parameters(parameters, grads)
  

  • 随机梯度下降：

  X = data_input  
  Y = labels  
  parameters = initialize_parameters(layers_dims)  
  for i in range(0, num_iterations):  
      for j in range(0, m):  
          a, caches = forward_propagation(X[:,j], parameters)  
          cost = compute_cost(a, Y[:,j])  
          grads = backward_propagation(a, caches, parameters)  
          parameters = update_parameters(parameters, grads)
  

  • 对于随机梯度下降，在更新梯度之前，只使用 1 个训练样例。
  • 当训练集大时，随机梯度下降可以更新的更快，但是这些参数会向最小值摆动而不是平稳地收敛。

• 小批量梯度下降 (Mini-batch)：

  • 如果既不使用整个训练集，也不使用一个训练示例，来执行每次更新，则通常会得到更快的结果。
  • 小批量梯度下降通常会胜过梯度下降或随机梯度下降，尤其是训练集较大时。

• 动量梯度下降 (Gradient Descent With Momentum)：

  • 传统的梯度下降在梯度下降过程中，振荡较大，每一点处的梯度只与当前方向有关，产生类似折线的效果，前进缓慢。
  • 动量梯度下降对梯度进行指数加权平均，使当前梯度不仅与当前方向有关，还与之前的方向有关。这样处理让梯度前进方向更加平滑，减少振荡，能够更快地到达最小值处。
  • 如果动量梯度下降的参数 \(\beta=0\)，则它变为没有冲量的标准梯度下降。\(\beta\) 越大，更新越平滑，我们对过去的梯度的考虑也更多。

• RMSprop：

  • 对于 \(w\) 和 \(b\)，如果哪个方向振荡大，就减小该方向的更新速度，从而减小振荡。

• Adam：

  • 结合了动量梯度下降和 RMSProp 的优点。

超参数 批标准化 编程框架

超参数调试

调试过程：

• 深度神经网络需要调试的超参数包括：
  • 学习因子 \(\alpha\)：通常来说是需要重点调试的超参数。
  • 动量梯度下降因子 \(\beta\)：通常来说重要程度仅次于 \(\alpha\)。
  • Adam 算法参数：\(\beta_1\)、\(\beta_2\)、\(\varepsilon\)。
  • 神经网络层数。
  • 各隐藏层神经元个数：通常来说重要程度仅次于 \(\alpha\)。
  • 学习因子下降参数 \(decay\_rate\)。
  • 批量训练样本包含的样本个数 \(mini\_batch\_size\)：通常来说重要程度仅次于 \(\alpha\)。
• 通常做法：
  • 随机化选择参数，尽可能地得到更多种参数组合。
  • 为得到更精确的最佳参数，放大表现较好的区域，对选定的区域进行由粗到细的采样。

为超参数选择合适的范围：

• 对于某些超参数，如神经网络层数、各隐藏层神经元个数，取值只能是正整数，可以进行随机均匀采样。

• 对于另一些参数，如学习因子 \(\alpha\)：

  • 设待调范围为 \([0.0001, 1]\)，如果随机均匀采样，则 \(90\%\) 的采样点分布在 \([0.1, 1]\)，但是 \(\alpha\) 的最佳取值更可能出现在 \([0.0001, 0.1]\)。

  • 因此可以采用取对数的方法，线性区间是 \([a, b]\)，对数区间是 \([m, n]\)：

    m = np.log10(a)
    n = np.log10(b)
    r = np.random.rand()
    r = m + (n - m) * r
    r = np.power(10, r)
    

• 除 \(\alpha\) 外，\(\beta\) 也不能随机均匀采样，因为 \(\beta\) 越接近 \(1\)，则对 \(1/(1 - \beta)\) 的影响越大。

超参数训练的实践：

Babysitting One Model 只对一个模型进行训练

Training Many Models In Parallel 对多个模型同时进行训练

批标准化

标准化网络中的激活函数：

Batch Normalization 批标准化

• 批标准化可以让调试超参数更加简单，让模型可接受的超参数范围更大。

• 在《标准化输入》一节对输入数据进行标准化，同样，可以对 \(l\) 层的输入，即 \(A^{[l - 1]}\) 或 \(Z^{[l - 1]}\) 标准化：

  \[\mu = \frac{1}{m} \sum_i z^{(i)} ,\quad \sigma^2 = \frac{1}{m} \sum_i(z_i - \mu)^2 ,\quad z_{norm}^{(i)} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2 + \varepsilon}} \]
  • \(m\) 是单个 Mini-batch 包含样本个数。
  • \(\varepsilon\) 是为了防止分母为 \(0\)。

• 上式使得 \(z^{(i)}\) 均值为 \(0\)，方差为 \(1\)，但是实际并不希望这样，于是：

  \[\tilde z^{(i)} = \gamma \cdot z_{noem}^{(i)} + \beta \]
  • \(\gamma\) 和 \(\beta\) 同 \(w\) 和 \(b\) 一样是可以通过梯度下降等算法求得的参数。
  • 从激活函数的角度来讲，如果 \(z^{(i)}\) 的均值为 \(0\)，处于激活函数的线性区域，不利于训练好的非线性神经网络。

将 Batch Norm 应用于神经网络：

• 整体流程：

  \[X \xrightarrow{W^{[1]}, b^{[1]}} Z^{[1]} \xrightarrow[BN]{\beta^{[1]}, \gamma^{[1]}} \tilde Z^{[1]} \rightarrow A^{[1]} \rightarrow \cdots \rightarrow A^{[L - 1]} \xrightarrow{W^{[L]}, b^{[L]}} Z^{[L]} \xrightarrow[BN]{\beta^{[L]}, \gamma^{[L]}} \tilde Z^{[L]} \rightarrow A^{[L]} \]

• 在 BN 中，参数 \(b\) 可以删去，需要使用梯度下降求的参数只有 \(W\)、\(\gamma\) 和 \(beta\)。

Batch Norm 为什么凑效：

Covariate Shift 列分布差异

• Batch Norm 减少了各层 \(W^{[l]}\)、\(B^{[l]}\) 之间的耦合性，让各层更加独立。
• Batch Norm 起到了轻微正则化的作用。

Batch Norm 在测试集上的使用：

• 在训练时 \(\mu\) 和 \(\sigma\) 是通过单个 Mini-batch 中的 \(m\) 个样本求得的，测试时，如果只有一个样本，求其均值和方差是没有意义的，这就要对 \(\mu\) 和 \(\sigma\) 进行估计。
• 方法一：将所有训练集放入最终的神经网络模型中，将每个隐藏层计算得到的 \(\mu^{[l]}\) 和 \(\sigma^{[l]}\) 直接作为测试过程的 \(\mu^{[l]}\) 和 \(\sigma^{[l]}\) 来使用。实际应用中一般不使用这种方法。
• 方法二：对于第 \(l\) 层隐藏层，考虑所有 Mini-batch 在该隐藏层下的 \(\mu^{[l]}\) 和 \(\sigma^{[l]}\)，然后用指数加权平均的方式来预测得到当前单个样本的 \(\mu^{[l]}\) 和 \(\sigma^{[l]}\)。

多分类

Softmax 回归：

• 一般使用 Softmax 回归处理多分类问题，对于一个长度为 \(C\) 的任意实数向量，Softmax 可以把它压缩为一个长度为 \(C\) 的、取值在 \((0, 1)\) 区间的实数矢量，且矢量中各元素之和为 \(1\)，因此 Softmax 的输出可以作为概率。

• \(C\) 代表种类个数。

• 神经网络输出层有 \(C\) 个神经元，每个神经元的输出 \(a_i^{[L]}\) 依次对应属于该类的概率。

  \[a_i^{[L]} = \frac{e^{z_i^{[L]}}}{\sum_{i=1}^{[L]}e^{z_i^{[L]}}} \]

• 所有的 \(a_i^{[L]}\) 组成 \(\hat y\)，\(\hat y\) 维度为 \((C, 1)\)。

训练一个 Softmax 分类器：

• 对于 \(C=4\) 的多分类，损失函数为：
  \[L(\hat y, y)= -\sum_{j=1}^4 y_j \cdot \log \hat y_j \]
  代价函数为：
  \[J = \frac{1}{m}\sum_{i=1}^m L(\hat y, y) \]
  输出层反向传播的计算：
  \[dZ^{[L]} = A^{[L]} - Y \]

编程框架

编程框架：

• PaddlePaddle / Tensorflow / Torch

Tensorflow：

import numpy as np
import tensorflow as tf

cofficients = np.array([[1.],[-10.],[25.]])
w = tf.Variable(0,dtype=tf.float32)
x = tf.placeholder(tf.float32,[3,1])
cost = x[0][0]*w**2 + x[1][0]*w + x[2][0]
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

init = tf.global_variables_initializer()
session = tf.Session()
session.run(init)
print(session.run(w))

for i in range(1000):
    session.run(train, feed_dict=(x:coefficients))
print(session.run(w))

'''
# 另一种写法
with tf.Session() as session:
    session.run(init)
    print(session.run(w))
'''

参考

• CSDN：完结篇 | 吴恩达 deeplearning.ai 专项课程精炼笔记全部汇总