【深度学习 - 吴恩达】L2W2作业

本文为吴恩达 Deep Learning 作业，Mini-batch，Momentum，Adam

数据

np.random.seed(3)
train_X, train_Y = datasets.make_moons(n_samples=300, noise=.2)

模型

模型结构：

​ 3 层神经网络：LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID。

​ 维度：layers_dims = [train_X.shape[0], 5, 2, 1]。

Mini-batch

更新

• 与普通的梯度下降的更新相同。

def update_parameters_with_gd(parameters, grads, learning_rate):
    L = len(parameters) // 2
    for l in range(L):
        parameters["W" + str(l + 1)] = parameters \
        	["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]  # 重点
        parameters["b" + str(l + 1)] = parameters \
        	["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]  # 重点
    return parameters

构建小批次

• 将 X 和 Y 打乱，打乱时要保证 X 和 Y 是同步的。
• 将打乱后的 X 和 Y 分成 Mini-batch：
  • 每个 Mini-batch 的大小为 mini_batch_size = 64。
  • 一共有 math.floor(m / mini_batch_size) 个完整的 Mini-batch。
  • 和一个不完整的 Mini-batch，这个 Mini-batch 中有 m % mini_batch_size 个元素。

def random_mini_batches(X, Y, mini_batch_size=64, seed=0):
    np.random.seed(seed)
    m = X.shape[1]
    mini_batches = []

    permutation = list(np.random.permutation(m))
    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape((1, m))

    num_complete_minibatches = math.floor(m / mini_batch_size)
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[:, k * mini_batch_size: (k + 1) * mini_batch_size]
        mini_batch_Y = shuffled_Y[:, k * mini_batch_size: (k + 1) * mini_batch_size]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size: m]
        mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size: m]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    return mini_batches

Momentum

初始化

• 速度被初始化为 $0$。

def initialize_velocity(parameters):
    L = len(parameters) // 2
    v = {}
    for l in range(L):
        v["dW" + str(l + 1)] = np.zeros(parameters['W' + str(l + 1)].shape)
        v["db" + str(l + 1)] = np.zeros(parameters['b' + str(l + 1)].shape)
    return v

更新

$$V_{dW} = \beta \cdot V_{dW} + (1 − \beta) \cdot dW ,\quad V_{db} = \beta \cdot V_{db} + (1 − \beta) \cdot db \\ W = W - \alpha V_{dW} ,\quad b = b - \alpha V_{db}$$

def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
    L = len(parameters) // 2
    for l in range(L):
        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads['dW' + str(l + 1)]
        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads['db' + str(l + 1)]
        parameters["W" + str(l + 1)] = parameters['W' + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters['b' + str(l + 1)] - learning_rate * v["db" + str(l + 1)]
    return parameters, v

Adam

初始化

• v 和 s 被初始化为 $0$。

def initialize_adam(parameters):
    L = len(parameters) // 2
    v = {}
    s = {}
    for l in range(L):
        v["dW" + str(l + 1)] = np.zeros(parameters["W" + str(l + 1)].shape)
        v["db" + str(l + 1)] = np.zeros(parameters["b" + str(l + 1)].shape)
        s["dW" + str(l + 1)] = np.zeros(parameters["W" + str(l + 1)].shape)
        s["db" + str(l + 1)] = np.zeros(parameters["b" + str(l + 1)].shape)
    return v, s

更新

$$\begin{aligned} V_{dW} = \beta_1 V_{dW} + (1 − \beta_1)dW &,\quad V_{db} = \beta_1 V_{db} + (1 − \beta_1)db \\ S_{dW} = \beta_2 S_{dW} + (1 − \beta_2)dW^2 &,\quad S_{db} = \beta_2 S_{db} + (1 − \beta_2)db^2 \\ V^{corrected}_{dW} = \frac{V_{dW}}{1 − \beta^t_1} &,\quad V^{corrected}_{db} = \frac{V_{db}}{1 − \beta^t_1} \\ S^{corrected}_{dW} = \frac{S_{dW}}{1 − \beta^t_2} &,\quad S^{corrected}_{db} = \frac{S_{db}}{1 − \beta^t_2} \\ W := W − \alpha \frac{V^{corrected}_{dW}}{\sqrt{S^{corrected}_{dW}} + \varepsilon} &,\quad b := b − \alpha \frac{V^{corrected}_{db}}{\sqrt{S^{corrected}_{db}} + \varepsilon} \end{aligned}$$

def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8):
    L = len(parameters) // 2
    v_corrected = {}
    s_corrected = {}
    for l in range(L):
        v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * grads['dW' + str(l + 1)]
        v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads['db' + str(l + 1)]
        v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - beta1 ** t)
        v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - beta1 ** t)
        s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * (grads['dW' + str(l + 1)] ** 2)
        s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * (grads['db' + str(l + 1)] ** 2)
        s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - beta2 ** t)
        s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - beta2 ** t)
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - \
        	learning_rate * (v_corrected["dW" + str(l + 1)] / np.sqrt(s_corrected["dW" + str(l + 1)] + epsilon))
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - \
        	learning_rate * (v_corrected["db" + str(l + 1)] / np.sqrt(s_corrected["db" + str(l + 1)] + epsilon))
    return parameters, v, s

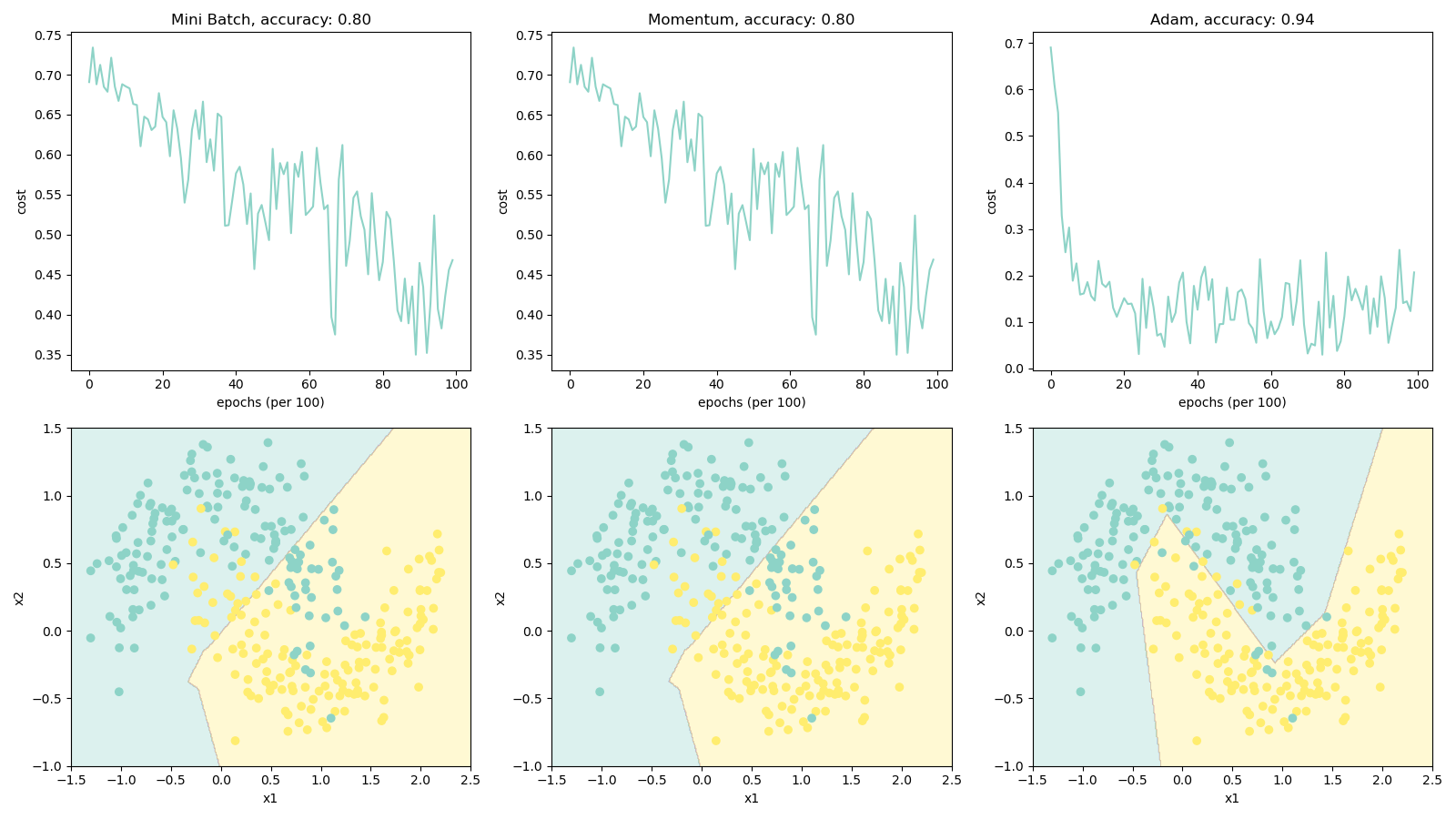
结果

• 动量梯度下降通常会有所帮助，但是鉴于学习率低和数据集过于简单，其影响几乎可以忽略不计。
• 损失的巨大波动是因为对于优化算法，某些小批处理比其他小批处理更为困难。
• Adam 明显胜过 Mini-batch 和动量梯度下降。如果在此简单数据集上运行更多 epoch，则这三种方法都将产生非常好的结果。但是，Adam收敛得更快。

关于 Python

np

np.random.permutation：

• 对序列进行随机排序。

• 例：

  np.random.seed(1)
  a = np.random.permutation(5)
  b = list(a)
  X = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
  print("a = " + str(a))
  print("b = " + str(b))
  print("X[:, b] = \n" + str(X[:, b]))
  

  输出：

  a = [2 1 4 0 3]
  b = [2, 1, 4, 0, 3]
  X[:, b] = 
  [[ 3  2  5  1  4]
   [ 8  7 10  6  9]]