【Deep Learning】L2W1作业
本文为吴恩达 Deep Learning 作业，初始化，正则化，梯度检验
初始化
数据
np.random.seed(1)
train_X, train_Y = datasets.make_circles(n_samples=300, noise=.05)
模型
模型结构：
3 层神经网络：
LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID。 维度：
layers_dims = [X.shape[0], 10, 5, 1]。
初始化
def initialize_parameters_zeros(layers_dims):
parameters = {}
L = len(layers_dims) # number of layers in the network
for l in range(1, L):
parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l - 1])) # 重点
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
def initialize_parameters_random(layers_dims):
np.random.seed(3) # This seed makes sure your "random" numbers will be the as ours
parameters = {}
L = len(layers_dims) # integer representing the number of layers
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * 10 # 重点
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
def initialize_parameters_he(layers_dims):
np.random.seed(3)
parameters = {}
L = len(layers_dims) - 1 # integer representing the number of layers
for l in range(1, L + 1):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2. / layers_dims[l - 1]) # 重点
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
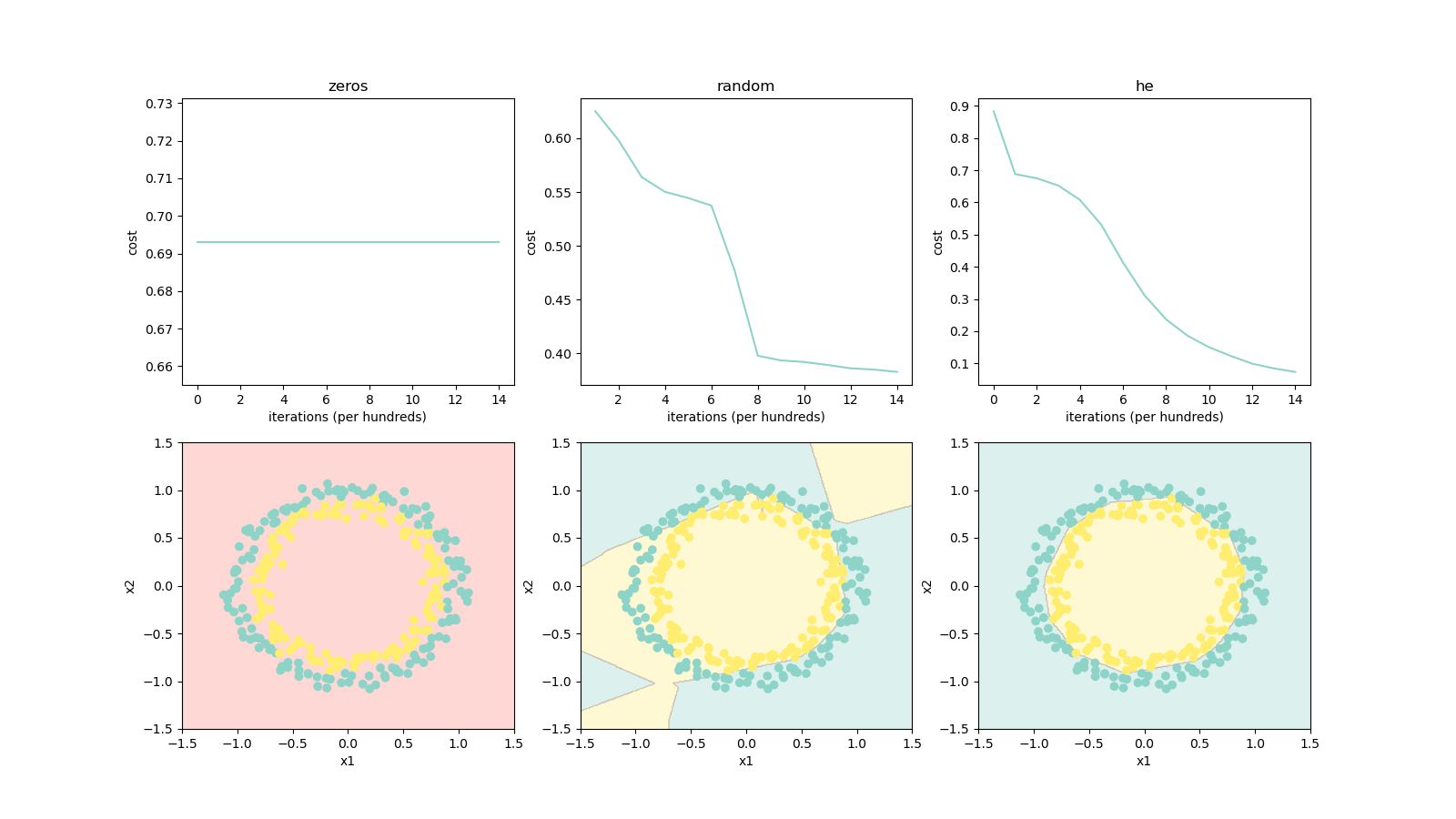
结果
- 将所有权重初始化为零会导致网络无法打破对称性，每一层中的每个神经元都将学习相同的东西。
- 如果将权重随机初始化为非常大的值：
- 损失一开始很高，因为随机权重值较大，对于某些数据，最后一层激活函数 \(Sigmoid\) 输出的结果非常接近 \(0\) 或 \(1\)，并且当该示例数据预测错误时，将导致非常高的损失。
- 初始化不当会导致梯度消失或梯度爆炸，同时也会减慢优化算法的速度。
- 训练较长时间的网络，将会看到更好的结果，但是使用太大的随机数进行初始化会降低优化速度。
正则化
数据
def load_2D_dataset():
data = scipy.io.loadmat('data.mat')
train_X = data['X'].T
train_Y = data['y'].T
test_X = data['Xval'].T
test_Y = data['yval'].T
return train_X, train_Y, test_X, test_Y
模型
模型结构：
3 层神经网络：
LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID。 维度：
layers_dims = [X.shape[0], 20, 3, 1]。
L2 正则化
使用 L2 正则化时，需要修改 “代价计算” 和 “反向传播” 函数。
代价计算：
-
L2 正则化的公式为：
\[J(w^{[1]}, b^{[1]}, \cdots , w^{[L]}, b^{[L]}) = \frac{1}{m} \sum_{i = 1}^{m} L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \sum_{l=1}^L \left \| w^{[l]}\right \|_F^2 ,\quad \left \| w^{[l]} \right \|_F^2 = \sum_{i = 1}^{n^{[l]}} \sum_{j = 1}^{n^{[l-1]}}(w_{ij}^{[l]})^2 \]np.square将矩阵中的每一项求平方。np.sum将矩阵中的每一项相加。- 一共有 \(3\) 层，所以
np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)。
def compute_cost_with_regularization(A3, Y, parameters, lambd):
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
# This gives you the cross-entropy part of the cost
cross_entropy_cost = compute_cost(A3, Y)
L2_regularization_cost = (1. / m * lambd / 2) * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) # 重点
cost = cross_entropy_cost + L2_regularization_cost
return cost
反向传播：
\[dw^{[l]} = dw^{[l]}_{before} + \frac{\lambda}{m}w^{[l]}
\]
def backward_propagation_with_regularization(X, Y, cache, lambd):
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1. / m * np.dot(dZ3, A2.T) + lambd / m * W3 # 重点
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T) + lambd / m * W2 # 重点
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T) + lambd / m * W1 # 重点
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
Dropout
使用 Dropout 时，需要修改 “正想传播” 和 “反向传播” 函数。
正向传播：
keep_prob是要保留的神经元比例。
def forward_propagation_with_dropout(X, parameters, keep_prob=0.5):
np.random.seed(1)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
D1 = np.random.rand(A1.shape[0], A1.shape[1]) # 重点
D1 = D1 < keep_prob # 重点, 这一步将 D1 中的值转换为 0 或 1
A1 = A1 * D1 # 重点
A1 = A1 / keep_prob # 重点, 使下一层神经元的输入值尽量保持不变
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
D2 = np.random.rand(A2.shape[0], A2.shape[1]) # 重点
D2 = D2 < keep_prob # 重点
A2 = A2 * D2 # 重点
A2 = A2 / keep_prob # 重点
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
反向传播：
- 在反向传播中，将将相同
D1、D2重新应用于dA1、dA2来关闭相同的神经元。 - 在反向传播中，将
dA1除以keep_prob，因为正向传播时，A1被keep_prob缩放，所以其派生的dA1也由相同的keep_prob缩放。
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1. / m * np.dot(dZ3, A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dA2 = dA2 * D2 # 重点
dA2 = dA2 / keep_prob # 重点
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1 # 重点
dA1 = dA1 / keep_prob # 重点
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
结果
- 正则化将帮助减少过拟合。
- 正则化将使权重降低到较低的值。
- L2 正则化和 Dropout 是两种非常有效的正则化技术。
- L2 正则化基于以下假设：权重较小的模型比权重较大的模型更简单。因此，通过对损失函数中权重的平方值进行惩罚，可以将所有权重驱动为较小的值。\(\lambda\) 太大会使损失过高，这将导致模型更平滑，输出随着输入的变化而变化得更慢。
- 仅在训练期间使用 Dropout，在测试期间不要使用。
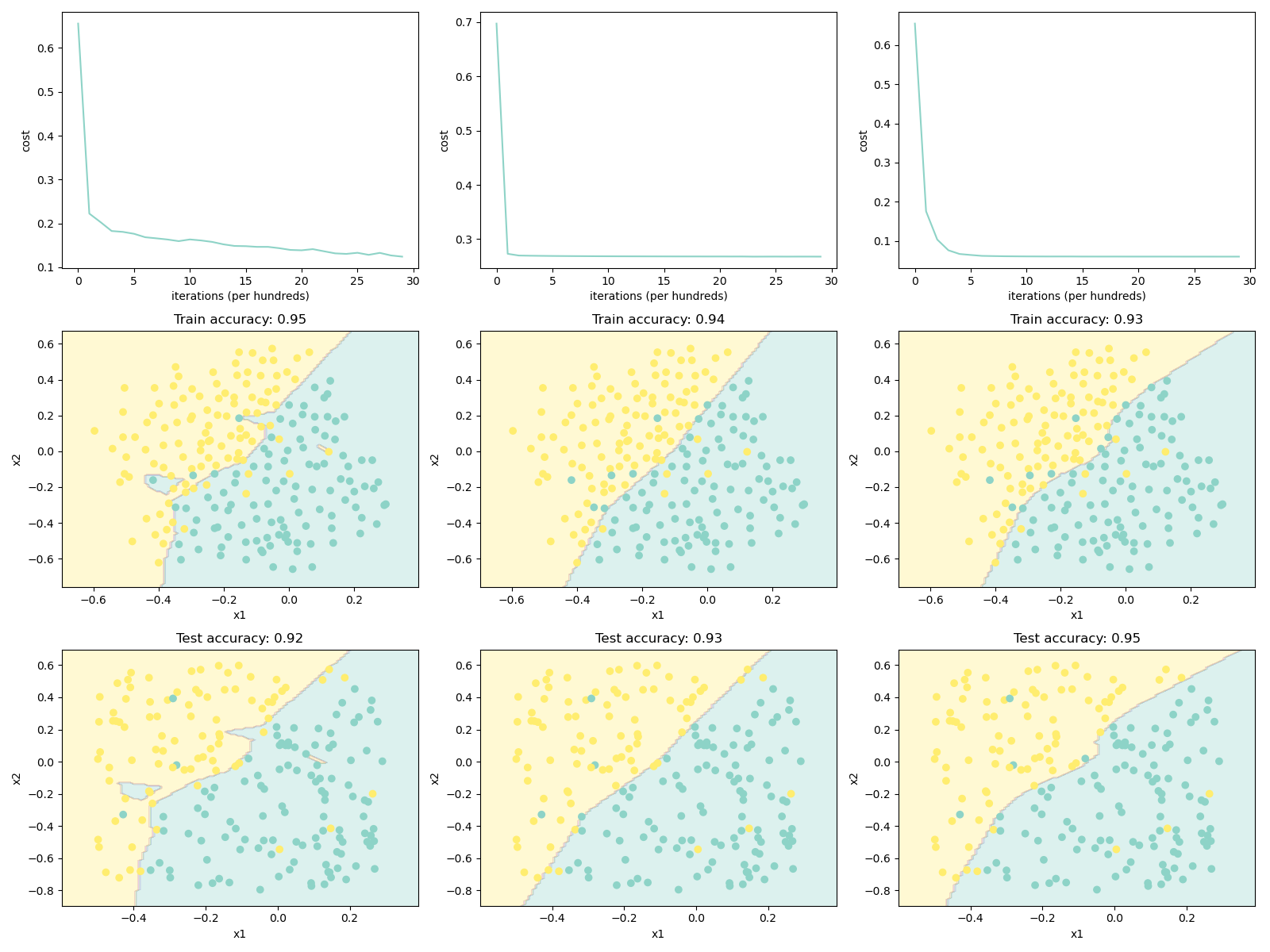
- 下图从左到右为：不使用正则化、L2 正则化、Dropout。
梯度检验
一维梯度检验
-
gradapporx是用公式 \(g(\theta) = (f(\theta + \varepsilon) - f(\theta - \varepsilon)) / 2\varepsilon\) 计算得到的梯度。 -
grad是用反向传播得到的公式。 -
比较二者相似度：
\[\frac{\left \| d\theta_{approx} - d\theta \right \|_2}{\left \| d\theta_{approx} \right \|_2 + \left \| d\theta \right \|_2} \]np.linalg.norm求范数，默认是二范数 \(\sqrt{x_1^2 + x_2^2 + \cdots + x_n^2}\)。
def gradient_check(x, theta, epsilon=1e-7):
thetaplus = theta + epsilon # 重点
thetaminus = theta - epsilon # 重点
J_plus = forward_propagation(x, thetaplus) # 重点
J_minus = forward_propagation(x, thetaminus) # 重点
gradapprox = (J_plus - J_minus) / (2 * epsilon) # 重点
grad = backward_propagation(x, theta) # 重点
numerator = np.linalg.norm(grad - gradapprox) # 重点
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # 重点
difference = numerator / denominator # 重点
if difference < 1e-7:
print("The gradient is correct!")
else:
print("The gradient is wrong!")
return difference
N 维梯度检验
dictionary_to_vector和gradients_to_vector将字典转换成向量，vector_to_dictionary将向量转换成字典。- 字典：
paramaters = {"W1":..., "b1":..., ..., "b3":...}。 - 向量：
values = (W11, W12, ...W154, ..., b31)。
- 字典：
def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7):
grad = gradients_to_vector(gradients)
parameters_values, _ = dictionary_to_vector(parameters)
num_parameters = parameters_values.shape[0]
J_plus = np.zeros((num_parameters, 1))
J_minus = np.zeros((num_parameters, 1))
gradapprox = np.zeros((num_parameters, 1))
for i in range(num_parameters):
thetaplus = np.copy(parameters_values)
thetaplus[i][0] = thetaplus[i][0] + epsilon
J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaplus))
thetaminus = np.copy(parameters_values)
thetaminus[i][0] = thetaminus[i][0] - epsilon
J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus))
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2. * epsilon)
numerator = np.linalg.norm(grad - gradapprox)
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
difference = numerator / denominator
if difference > 1e-7:
print("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
else:
print("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
return difference
关于 Python
np
np.reshape：
numpy.reshape(a, newshape, order='C')
- 改变数组的形状。
a：要重塑的数组。newshape：新形状，维度为-1时，则从数组的长度和其他维度推断出此处的维度。
np.concatenate：
numpy.concatenate((a1, a2, ...), axis=0, out=None, dtype=None, casting="same_kind")
- 对数组进行拼接。
a1、a2：要拼接的数组。axis：等于 0 时，沿着第 0 个下标变化的方向进行操作。
