【Deep Learning】01 神经网络与深度学习

本文为吴恩达 Deep Learning 笔记

深度学习概述

什么是神经网络：

Neural Network 神经网络

Neuron 神经元

Rectified Linear Unit (ReLU) 线性整流函数

• 房价预测案例：

  • 该神经网络的输入 \(x\) 是房屋面积，输出 \(y\) 是房屋价格。
  • 中间包含了一个神经元，该神经元的功能就是实现函数 \(f(x)\) 的功能。

• ReLU：

  \[f(u) = \max(0, u) \]

用神经网络进行监督学习：

Supervised Learning / Unsupervised Learning 监督学习 / 无监督学习

Structured Data / Unstructured Data 结构化 / 非结构化数据

Convolution Neural Network (CNN) 卷积神经网络

Recurrent Neural Network (RNN) 循环神经网络

• 一些深度学习的应用案例：房价预测、广告投送、图像识别、语音识别、智能翻译、自动驾驶。
• 结构化数据和非结构化数据：
  • 结构化数据：表格。
  • 非结构化数据：图像、语音、文字。

为什么深度学习会兴起：

• 人类进入了大数据时代，传统机器学习算法在数据量较大的时候，性能一般，很难再有提升；而深度学习模型由于网络复杂，对大数据的处理和分析非常有效。
• 三要素：
  • 数据量的增加。
  • 算力的增强。
  • 算法的改进，例如将激活函数从 Sigmoid 改为 ReLU。

神经网络基础

二分分类与逻辑回归

二分分类：

Binary Classification 二分分类

• 二分类就是输出 \(y\) 只有 \(\{0, 1\}\) 两个离散值，如：判断图片中是否有猫存在。
• 符号：
  • \((x, y)\) 单个样本， \(x\) 是 \(n_x\) 维列向量，\(y \in \{0, 1\}\)。
  • \(m\) 样本数量，\(m_{train}\) 训练集样本数量，\(m_{test}\) 测试集样本数量 。
  • \(X\) 是 \(n_x\) 行 \(m\) 列矩阵，\(X = (x^{(1)}, x^{(2)}, \cdots, x^{(m)})\)。
  • \(Y\) 是 \(m\) 维行向量，\(Y = (y^{(1)}, y^{(2)}, \cdots, y^{(m)})\)。

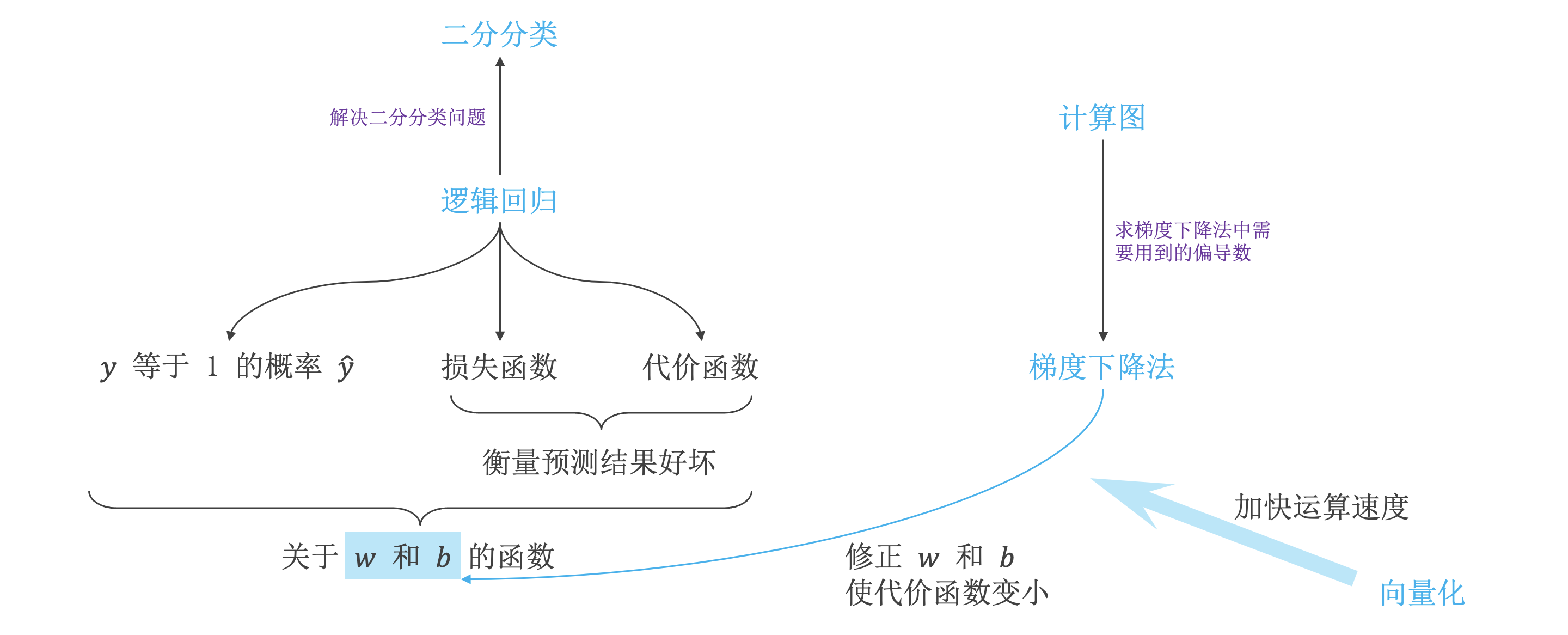
逻辑回归：

Logistic Regression 逻辑回归

Activation Function 激活函数

• 逻辑回归是一种广义的线性回归分析模型，属于机器学习中的监督学习，其推导过程与计算方式类似于回归的过程，但实际上主要是用来解决二分类问题（也可以解决多分类问题）。

• 当逻辑回归应用于二分类问题时，输出是概率 \(P(y = 1 | x)\)，即给定 \(x\)，该样本属于类别 \(1\) 的概率。

• 激活函数是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

• 符号：

  • \(\hat{y}\) 表示 \(y = 1\) 的概率，\(\hat{y} \in \{0, 1\}\)。
  • 参数 \(w\)，参数 \(b\)。
  • \(w\) 和 \(x\) 是 \(n\) 维列向量。

• 公式：

  • \(\hat{y} = w^\mathrm{T} x + b\)，这样并没有保证 \(\hat{y} \in \{0, 1\}\)。

  • \(\hat{y} = Sigmoid(w^\mathrm{T} x + b)\)，从而 \(\hat{y} \in \{0, 1\}\)。

  • \(Sigmoid(z)\) 函数，值域为 \([0, 1]\)，\(z \rightarrow -\infty\) 时 \(Sigmoid \rightarrow 0\)，\(z \rightarrow +\infty\) 时 \(Sigmoid \rightarrow1\)

    \[Sigmoid(z) = \sigma(z) = \frac{1}{1 + e ^{-z}} \]

    \(Sigmoid\) 求导：

    \[\begin{aligned} \sigma'(x) &= -\frac{1}{(1 + e^{-x})^2} \times (1 + e^{-x})' = \frac{1}{(1 + e^{-x})^2} \times (e^{-x}) \\ &= \frac{1}{1 + e^{-x}} \times \frac{e^{-x}}{1 + e^{-x}} = \frac{1}{1 + e^{-x}} \times \frac{1 + e^{-x} - 1}{1 + e^{-x}} = \sigma(x)(1 - \sigma(x)) \end{aligned} \]

逻辑回归代价函数：

Loss Function 损失函数

Cost Function 代价函数

• 符号：

  • \(x^{(i)}\)，\(y^{(i)}\) 表示第 \(i\) 个样本的 \(x\)，\(y\) 等变量值。

• 公式：

  • 损失函数 \(L(\hat{y}, y) = (\hat{y} - y)^2 / 2\)，这样是非凸的，可能会得到局部最优解。

  • 损失函数 \(L(\hat{y} - y) = -(y \log \hat{y} + (1 - y) \log (1 - \hat{y}))\)，当 \(y = 1\) 时，\(\hat y\) 越接近 \(1\)，预测效果越好；当 \(y = 0\) 时，\(\hat y\) 越接近 \(0\) 预测效果越好。损失函数越小越好。

    公式推导：咕咕咕～

  • 代价函数是损失函数的平均值，代价函数的目的是求出最佳的 \(w\) 和 \(b\)。

    \[J(w, b) = \frac{1}{m}\sum_{i = 1}^m L(\hat{y}^{(i)} - y^{(i)}) = -\frac{1}{m}\sum_{i = 1}^m [y^{(i)} \log \hat{y}^{(i)} + (1 - y^{(i)}) \log (1 - \hat{y}^{(i)})] \\ \hat{y} = Sigmoid(w^\mathrm{T} x + b) \]

梯度下降法与计算图

梯度下降法：

Gradient Descent 梯度下降法

• 梯度下降算法是先随机选择一组参数 \(w\) 和 \(b\) 值，然后每次迭代的过程中分别沿着 \(w\) 和 \(b\) 的梯度 (偏导数) 的反方向前进一小步，不断修正 \(w\) 和 \(b\)。每次迭代更新 \(w\) 和 \(b\) 后，都能让 \(J(w,b)\) 更接近全局最小值。

• 公式 (\(w\) 和 \(b\) 的修正表达式)：

  \[w := w − \alpha \frac{\partial J(w,b)}{\partial w} \\ b := b − \alpha \frac{\partial J(w,b)}{\partial b} \]
  • \(\alpha\) 是学习因子，表示梯度下降的步进长度。\(\alpha\) 越大，\(w\) 和 \(b\) 每次更新的“步伐”越大；\(\alpha\) 越小，\(w\) 和 \(b\) 每次更新的“步伐”越小。
  • 在编程中，常用 dw 表示对 \(w\) 求偏导，用 db 表示对 \(b\) 求偏导。

计算图：

Computation Graph 计算图

• 整个神经网络的训练过程实际上包含了两个过程：正向传播 (Forward Propagation) 和反向传播 (Back Propagation)。正向传播是从输入到输出，由神经网络计算得到预测输出的过程；反向传播是从输出到输入，对参数 \(w\) 和 \(b\) 计算梯度的过程。

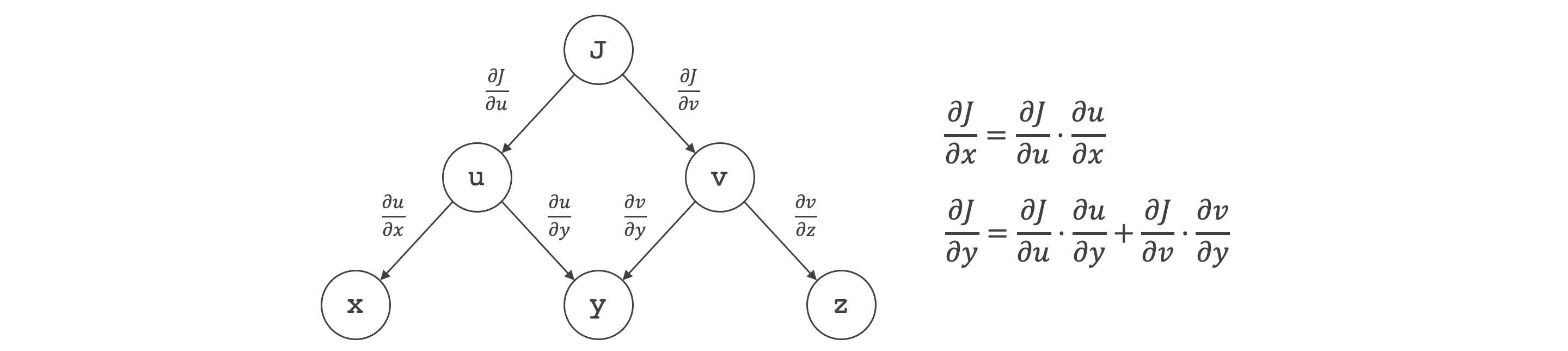
计算图求导数：

• 暂且把计算图理解成一种求导数的方法。
  • 有边 \(x\) 到 \(u\) 则可求得 \(u\) 对 \(x\) 的偏微分。
  • 对于每条从 \(x\) 到 \(J\) 的路径，所有边的微分相乘，求得该路径上的微分。
  • 从 \(x\) 到 \(J\) 有多条路径，将这些路径上的微分相加，求得 \(J\) 对 \(x\) 的偏微分。

逻辑回归与梯度下降法：

• 已知公式，假设 \(w\) 的维度是 \(2\)，有 \(w_1\) 和 \(w_2\)，：

  \[z = w^\mathrm{T} x + b = w_1x_1 + w_2x_2 + b\\ \hat{y} = a = \sigma(z) = \frac{1}{1 + e ^{-z}} \\ L(a, y) = -(y \log a + (1 - y) \log (1 - a)) \]

• 计算图：

• 推导过程：

  \[\frac{\partial L}{\partial a} = -\frac{y}{a} + \frac{1-y}{1-a} ,\quad \frac{\partial a}{\partial z} = a(1-a) ,\quad \frac{\partial z}{\partial w_1} = x_1 ,\quad \frac{\partial z}{\partial w_2} = x_2 ,\quad \frac{\partial z}{\partial b} = 1 \]

• 链式求导：

  \[\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial a} \frac{\partial a}{\partial z} \frac{\partial z}{\partial w_1} = x_1(a - y) ,\quad \frac{\partial L}{\partial w_2} = \frac{\partial L}{\partial a} \frac{\partial a}{\partial z} \frac{\partial z}{\partial w_2} = x_2(a - y) \\ \frac{\partial L}{\partial b} = \frac{\partial L}{\partial a} \frac{\partial a}{\partial z} \frac{\partial z}{\partial b} = a - y \\ \]

• 带入梯度下降算法 \(w\) 和 \(b\) 的修正表达式。

\(m\) 个样本的梯度下降：

• 当样本数增加后，\(w\) 和 \(b\) 的偏导数可以写成和平均的形式：

  \[\frac{\partial J}{\partial w_1} = \frac{1}{m} \sum_{i = 1}^{m} x_1^{(i)}(a^{(i)} - y^{(i)}) ,\quad \frac{\partial J}{\partial w_2} = \frac{1}{m} \sum_{i = 1}^{m} x_2^{(i)}(a^{(i)} - y^{(i)}) \\\frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i = 1}^{m} (a^{(i)} - y^{(i)}) \]

• 伪代码：

  J = 0; dw1 = 0; dw2 = 0; db = 0;
  for i = 1 to m
      z(i) = wx(i) + b;
      a(i) = sigmoid(z(i));
      J += - [y(i)log(a(i)) + (1 - y(i)log(1 - a(i));
      dz(i) = a(i) - y(i);
      dw1 += x1(i)dz(i);
      dw2 += x2(i)dz(i);
      db += dz(i);
  J /= m; dw1 /= m; dw2 /= m; db /= m;
  # 每次迭代后根据梯度下降算法对 w1, w2, b 进行更新
  

向量化

向量化引入：

Vectorization 向量化

• 向量化比 for 循环快很多。

向量化举例：

• 对于《\(m\) 个样本的梯度下降》这一节的伪代码，作出如下修改：

  J = 0; dw = np.zero((n-x, 1)); db = 0;
  for i = 1 to m
      z(i) = wx(i) + b;
      a(i) = sigmoid(z(i));
      J += - [y(i)log(a(i)) + (1 - y(i)log(1 - a(i));
      dz(i) = a(i) - y(i);
      dw += x(i)dz(i);  # n 维 w 向量不再需要用 for 循环来求
      db += dz(i);
  J /= m; dw /= m; db /= m;
  

向量化逻辑回归：

• 对于《逻辑回归与梯度下降法》这一节，有公式：

  \[z = w^\mathrm{T} x + b \\ a = \sigma(z) \]

• 对于 \(m\) 个样本，可以用 \(m\) 维行向量 \(Z\) （\(1\) 行 \(m\) 列）和 \(m\) 维行向量 \(A\) 来表示，\(X\) 是 \(n\) 行 \(m\) 列矩阵，\(w\) 是 \(n\) 维列向量：

  \[Z = w^\mathrm{T} X + b \\ A = \sigma(Z) \]

向量化逻辑回归的梯度下降结果：

• 对于《\(m\) 个样本的梯度下降》这一节的伪代码，作出如下修改：

  Z = np.dot(w.T, X) + b;
  A = sigmoid(Z);
  dZ = A - Y;
  dw = 1 / m * np.dot(X, dZ.T);
  db = 1 / m * np.sum(dZ);
  # 每次迭代后根据梯度下降算法对 w, b 进行更新, alpha 是学习因子
  w = w - alpha * dw
  b = b - alpha * db
  

浅层神经网络

神经网络

神经网络概述：

• 神经网络的结构与逻辑回归类似，只是神经网络的层数比逻辑回归多一层，多出来的中间那层称为隐藏层或中间层。
• 从计算上来说，神经网络的正向传播和反向传播过程只是比逻辑回归多了一次重复的计算。正向传播过程分成两层，第一层是输入层到隐藏层，用上标 \([1]\) 来表示；第二层是隐藏层到输出层，用上标 \([2]\) 来表示。

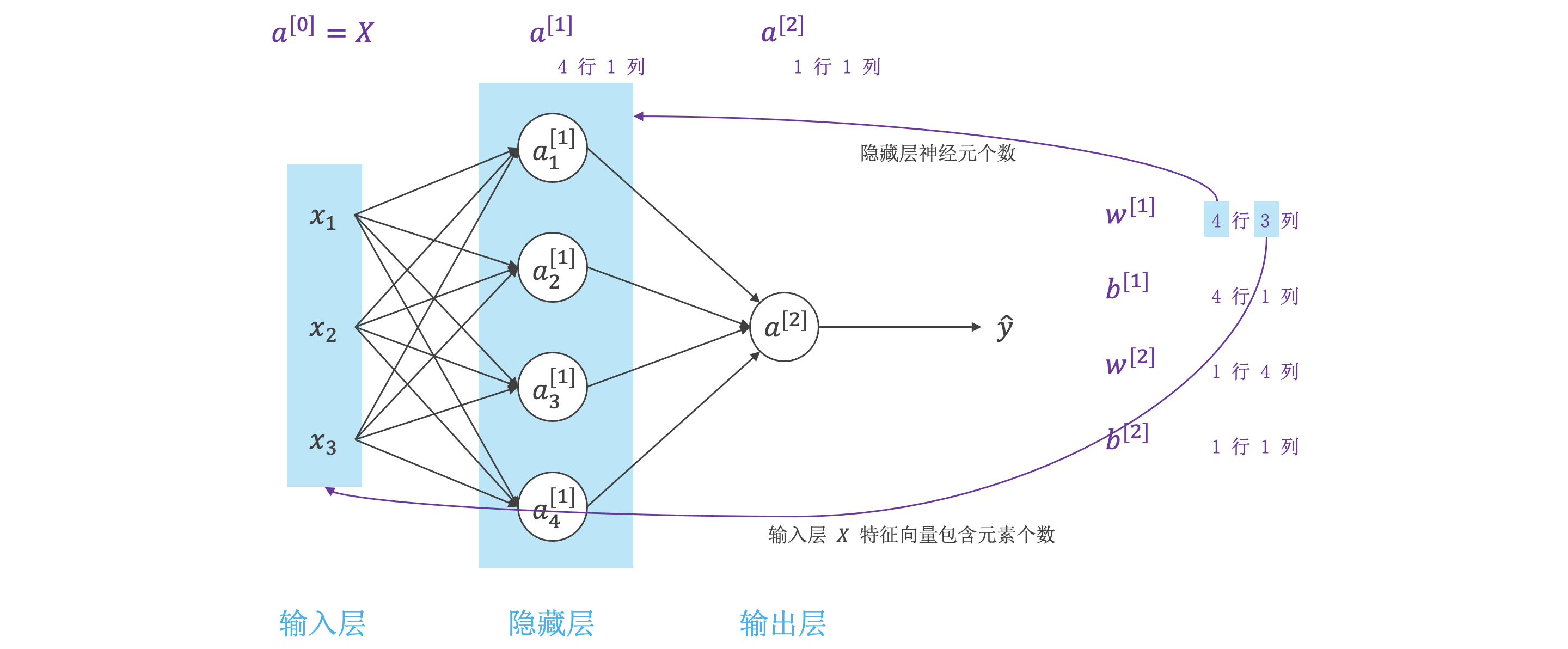
神经网络表示：

Shallow Neural Network 浅层神经网络

Input Layer 输入层

Hidden Layer 隐藏层

Output Layer 输出层

2 Layer NN 两层神经网络

计算神经网络的输出：

• 从输入层到输出层的公式：

  \[z^{[1]}_1 = w^{[1]\mathrm{T}}_1x + b^{[1]}_1,\quad a^{[1]}_1 = \sigma(z^{[1]}_1) \\ z^{[1]}_2 = w^{[1]\mathrm{T}}_2x + b^{[1]}_2,\quad a^{[1]}_2 = \sigma(z^{[1]}_2) \\ z^{[1]}_3 = w^{[1]\mathrm{T}}_3x + b^{[1]}_3,\quad a^{[1]}_3 = \sigma(z^{[1]}_3) \\ z^{[1]}_4 = w^{[1]\mathrm{T}}_4x + b^{[1]}_4,\quad a^{[1]}_4 = \sigma(z^{[1]}_4) \\ \]

• 从隐藏层到输出层的公式：

  \[z^{[2]}_1 = w^{[2]\mathrm{T}}_1a^{[1]} + b^{[2]}_1,\quad a^{[2]}_1 = \sigma(z^{[2]}_1) \]

• 向量化：

  \[\begin{aligned} z^{[1]} = W^{[1]}x + b^{[1]} &,\quad a^{[1]} = \sigma(z^{[1]}) \\ z^{[2]} = W^{[2]}a^{[1]} + b^{[2]} &,\quad a^{[2]} = \sigma(z^{[2]}) \end{aligned} \]

  其中：

  \[W^{[1]} = \begin{bmatrix} w^{[1]\mathrm{T}}_1 \\ w^{[1]\mathrm{T}}_2 \\ w^{[1]\mathrm{T}}_3 \\ w^{[1]\mathrm{T}}_4 \end{bmatrix} ,\quad W^{[2]} = \begin{bmatrix} w^{[2]\mathrm{T}}_1 \end{bmatrix} \]

\(m\) 个样本的神经网络：

• 向量化：

  \[\begin{aligned} Z^{[1]} = W^{[1]}X + b^{[1]} &,\quad A^{[1]} = \sigma(Z^{[1]}) \\ Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]} &,\quad A^{[2]} = \sigma(Z^{[2]}) \end{aligned} \]

  • \(Z^{[1]}\) 和 \(A^{[1]}\) 的维度是 \((4, m)\)，\(4\) 是隐藏层神经元的个数，\(m\) 是样本个数。

  • \(W^{[1]}\) 的维度是 \((4, n)\)，\(X\) 的维度是 \((n, m)\)，\(n\) 是输入特征向量包含的元素个数。

    输入矩阵 \(X\) 也可以写成 \(A^{[0]}\)。

  • \(Z^{[2]}\) 和 \(A^{[2]}\) 的维度是 \((1, m)\)。

向量化实现的解释：

• 略。

激活函数

激活函数：

\[\begin{aligned} sigmoid: a = \frac{1}{1 + e^{-z}} &,\quad ReLU: a = \max(0, z)& \\ tanh:a = \frac{e^z - e^{-z}}{e^z + e^{-z}} &,\quad Leaky ReLU: a = \max(0.01z, z) \end{aligned} \]

为什么需要使用非线形激活函数：

• 即便是包含多层隐藏层的神经网络，如果使用线性函数作为激活函数，最终的输出仍然是输入 \(x\) 的线性模型。这样的话神经网络就没有任何作用了。因此，隐藏层的激活函数必须要是非线性的。

激活函数的导数：

\[\begin{aligned} sigmoid: a'=a(1-a) &,\quad ReLU: a'=\left\{\begin{matrix} 0 & z < 0 \\ 1 & z \geq 0 \end{matrix}\right.\\ tanh: a' = 1 - a^2 &,\quad LeakyReLU: a'=\left\{\begin{matrix} 0.01 & z < 0 \\ 1 & z \geq 0 \end{matrix}\right.\\ \end{aligned} \]

梯度下降

神经网络的梯度下降法：

• 只列公式（与《向量化逻辑回归的梯度下降结果》这一节的伪代码有相似之处）：

dZ2 = A2 - Y
dW2 = 1 / m * np.dot(dZ2, A1.T)
db2 = 1 / m * np.sum(dZ2, axis = 1, keepdims = True)
dZ1 = np.dot(W2.T, dZ2) * g_(Z[1]);  # g_ 是激活函数的导数
dW1 = 1 / m * np.dot(dZ1, X.T)
db1 = 1 / m * np.sum(dZ1, axis = 1, keepdims = True)

直观理解反向传播：

• 咕咕咕～

初始化

随机初始化：

• 如果初始化为 \(0\)，隐藏层的神经元每次迭代更新得到相同的结果，完全对称，这样设置多个神经元没有意义。

• 随机初始化时将 \(W\) 随机初始化，\(b\) 可以初始化为 \(0\)，例：

  W1 = np.random.randn((2, 2)) * 0.01
  b1 = np.zero((2, 1))
  W2 = np.random.randn((1,2)) * 0.01
  b2 = 0
  

• \(W\) 初始化的值最好应较小，因为，如果使用 sigmoid 或 tanh 做激活函数，在 \(0\) 附近梯度较大，可以尽快找到全剧最优解。

深层神经网络

深层神经网络：

• \(L\) Layer NN 包含 \(L - 1\) 个隐藏层。
• \(n^{[l]}\) 表示第 \(l\) 层包含的神经单元个数，\(a^{[l]}\) 表示第 \(l\) 层的激活函数，\(l = 1, 2, \cdots, L\)。

深层神经网络中的向前传播：

• 对于第 \(l\) 层：
  \[Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]} \\ A^{[l]} = g^{[l]}(Z^{[l]}) \]

核对矩阵的维数：

• 对于单个训练样本：
  • \(x\) 的维度是 \((n^{[0]}, 1)\)。
  • \(W^{[l]}\)、\(dW^{[l]}\) 的维度是 \((n^{[l]}, n^{[l - 1]})\)。
  • \(b^{[l]}\)、\(db^{[l]}\) 的维度是 \((n^{[l]}, 1)\)。
  • \(z^{[l]}\)、\(a^{[l]}\) 的维度是 \((n^{[l]}, 1)\)。
• 对于 \(m\) 个训练样本：
  • \(x\) 的维度是 \((n^{[0]}, m)\)。
  • \(W^{[l]}\)、\(dW^{[l]}\) 的维度是 \((n^{[l]}, n^{[l - 1]})\)。
  • \(b^{[l]}\)、\(db^{[l]}\) 的维度是 \((n^{[l]}, 1)\)。
  • \(Z^{[l]}\)、\(A^{[l]}\) 的维度是 \((n^{[l]}, m)\)。

为什么使用深层表示：

• 人脸识别、语音识别、电路的例子。
• 处理同一逻辑问题，深层网络所需的神经元个数比浅层网络要少很多。

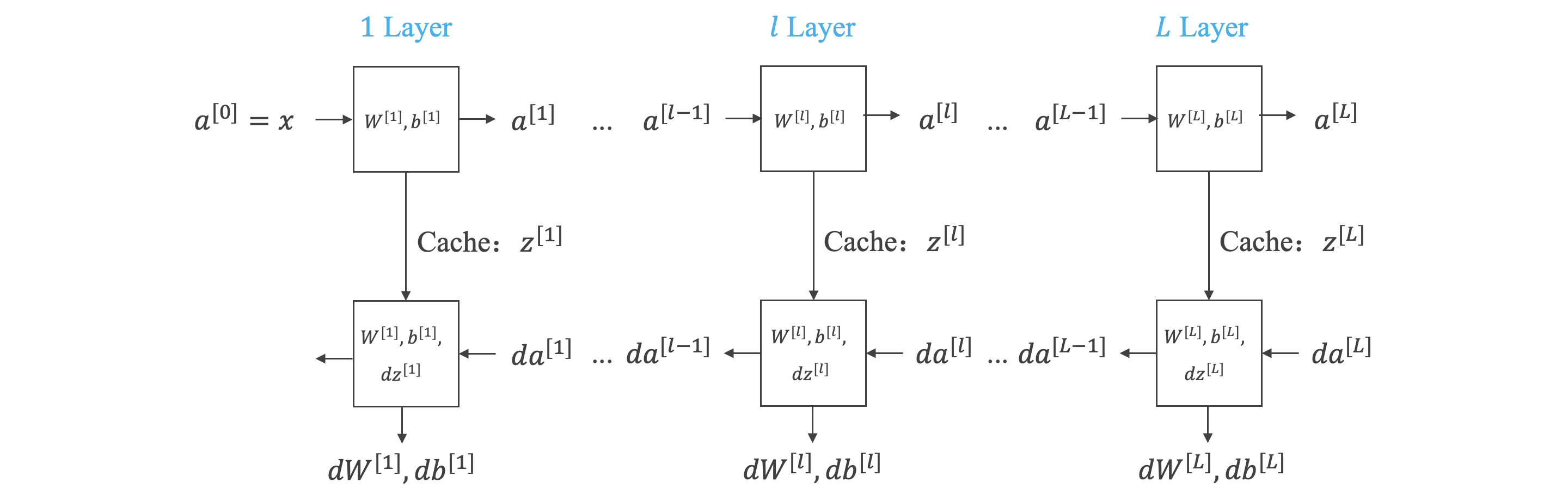
搭建深层神经网络块：

向前和向后传播：

• 向前传播，见《深层神经网络中的向前传播》一节。

• 向后传播：

  \[dZ^{[l]} = dA^{[l]} * g^{[l]'}(Z^{[l]}) \\ dW^{[l]} = \frac{1}{m}dZ^{[l]} \cdot A^{[l-1]\mathrm{T}} \\ db^{[l]} = \frac{1}{m} \sum_{i=1}^m dZ^{[l](i)} \\ dA^{[l-1]} = W^{[l]\mathrm{T}} \cdot dZ^{[l]} \]

• 伪代码：

  # 如果激活函数是 sigmoid
  def sigmoid_backward(dA, cache):
      Z = cache
      s = 1 / (1 + np.exp(-Z))
      dZ = dA * s * (1 - s)
      return dZ
  
  
  # 如果激活函数是 ReLU
  def relu_backward(dA, cache):
      Z = cache
      dZ = np.array(dA, copy=True)
      dZ[Z <= 0] = 0
      return dZ
  
  
  dW = 1 / m * np.dot(dZ, A_prev.T)
  db = 1 / m * np.sum(dZ, axis = 1, keepdims = True)
  dA_prev = np.dot(W.T, dZ) 
  

参数和超参数：

Parameters 参数

Hyperparameters 超参数

• 参数：\(W^{[l]}\)、\(b^{[l]}\)。
• 超参数：学习速率 \(\alpha\)、训练迭代次数 \(N\)、神经网络层数 \(L\)、各层神经元个数 \(n^{[l]}\)、激活函数 \(g(z)\)。

这和大脑有什么关系：

• 略。

参考

• CSDN：完结篇 | 吴恩达 deeplearning.ai 专项课程精炼笔记全部汇总