【Deep Learning】L1W3作业
本文为吴恩达 Deep Learning 作业，浅层神经网络
获得数据
X, Y = load_planar_dataset()
show_data(X, Y)
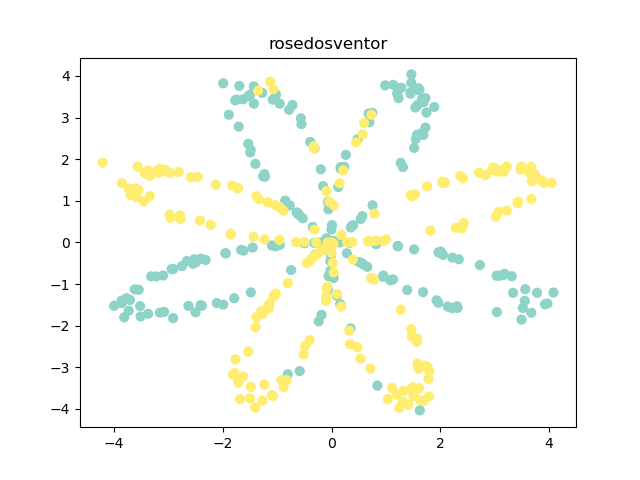
def show_data(X, Y):
plt.scatter(X[0, :], X[1, :], c=Y.reshape(X[0, :].shape), s=40, cmap='Set3')
plt.title("rosedosventor")
plt.show()
def load_planar_dataset():
np.random.seed(1)
m = 400 # number of examples
N = int(m / 2) # number of points per class
D = 2 # dimensionality
X = np.zeros((m, D)) # data matrix where each row is a single example
Y = np.zeros((m, 1), dtype='uint8') # labels vector (0 for red, 1 for blue)
a = 4 # maximum ray of the flower
for j in range(2): # 玫瑰线
ix = range(N * j, N * (j + 1))
t = np.linspace(j * 3.12, (j + 1) * 3.12, N) + np.random.randn(N) * 0.2 # theta
r = a * np.sin(4 * t) + np.random.randn(N) * 0.2 # radius
X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
Y[ix] = j
X = X.T
Y = Y.T
return X, Y
- 样本数量 \(m = 400\)。
- \(X\) 维度 \(n = 2\)。
- \(Y = 0\) 或 \(Y=1\)，对应的点为绿色或黄色，每种颜色的点各 \(200\) 个。
主要算法
神经网络结构
def layer_sizes(X, Y):
n_x = X.shape[0] # size of input layer
n_h = 4
n_y = Y.shape[0] # size of output layer
return n_x, n_h, n_y
- 输入层维度
n_x为 \(2\)，隐藏层维度n_h为 \(4\)（自定义），输出层维度n_y为 \(1\)。
初始化
def initialize_parameters(n_x, n_h, n_y):
np.random.seed(2)
W1 = np.random.randn(n_h, n_x) * 0.01 # 重点
b1 = np.zeros((n_h, 1)) # 重点
W2 = np.random.randn(n_y, n_h) * 0.01 # 重点
b2 = np.zeros((n_y, 1)) # 重点
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2}
return parameters
W1的维度是(n_h, n_x)，b1的维度是(n_h, 1)，W2的维度是(n_y, n_h)，b2的维度是(n_y, 1)。
向前传播
def forward_propagation(X, parameters):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1 = np.dot(W1, X) + b1 # 重点
A1 = np.tanh(Z1) # 重点
Z2 = np.dot(W2, A1) + b2 # 重点
A2 = sigmoid(Z2) # 重点
assert (A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1, "A1": A1, "Z2": Z2, "A2": A2}
return A2, cache
计算代价
def compute_cost(A2, Y):
m = Y.shape[1] # number of example
logProbs = Y * np.log(A2) + (1 - Y) * np.log(1 - A2) # 重点
cost = -1 / m * np.sum(logProbs) # 重点
cost = np.squeeze(cost) # makes sure cost is the dimension we expect.
assert (isinstance(cost, float))
return cost
反向传播
def backward_propagation(parameters, cache, X, Y):
m = X.shape[1]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2 = A2 - Y # 重点
dW2 = 1 / m * np.dot(dZ2, A1.T) # 重点
db2 = 1 / m * np.sum(dZ2, axis=1, keepdims=True) # 重点
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2)) # 重点
dW1 = 1 / m * np.dot(dZ1, X.T) # 重点
db1 = 1 / m * np.sum(dZ1, axis=1, keepdims=True) # 重点
grads = {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}
return grads
更新
def update_parameters(parameters, grads, learning_rate=1.2):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
W1 = W1 - learning_rate * dW1 # 重点
b1 = b1 - learning_rate * db1 # 重点
W2 = W2 - learning_rate * dW2 # 重点
b2 = b2 - learning_rate * db2 # 重点
parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2}
return parameters
整合
def nn_model(X, Y, n_h, num_iterations=10000, print_cost=False):
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x, n_h, n_y)
for i in range(0, num_iterations): # 重点
A2, cache = forward_propagation(X, parameters) # 重点
cost = compute_cost(A2, Y) # 重点
grads = backward_propagation(parameters, cache, X, Y) # 重点
parameters = update_parameters(parameters, grads) # 重点
if print_cost and i % 1000 == 0:
print("Cost after iteration %i: %f" % (i, cost))
return parameters
结果
预测
def predict(parameters, X):
A2, cache = forward_propagation(X, parameters)
predictions = np.round(A2)
return predictions
main 函数
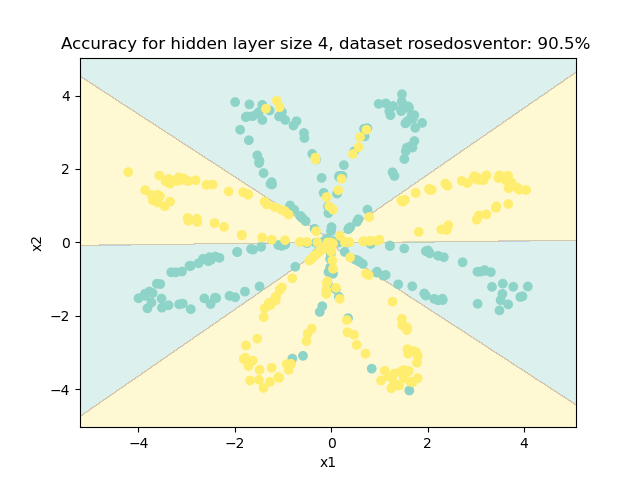
def main():
X, Y = load_planar_dataset()
show_data(X, Y)
parameters = nn_model(X, Y, 4)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Accuracy for hidden layer size 4, dataset rosedosventor: {}% ".format(accuracy))
plt.show()
绘图
def plot_decision_boundary(model, X, Y):
# Set min and max values and give it some padding
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1 # 横坐标的最小值和最大值
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1 # 纵坐标的最小值和最大值
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, alpha=0.3, cmap='Set3')
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(X[0, :], X[1, :], c=Y.reshape(X[0, :].shape), cmap='Set3')
拓展
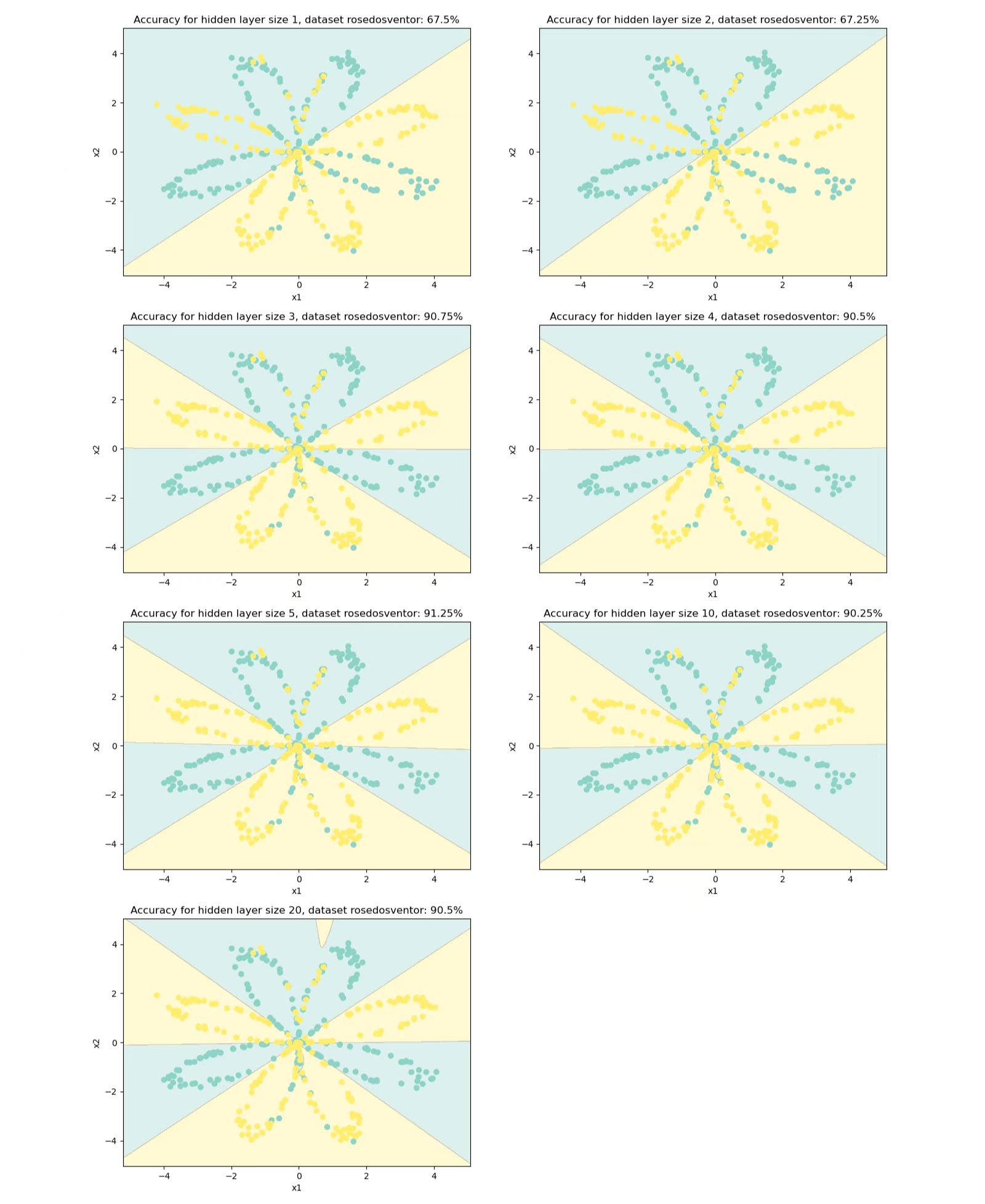
隐藏层大小的选择
def main():
X, Y = load_planar_dataset()
plt.figure(figsize=(16, 24))
hidden_layer_sizes = [1, 2, 3, 4, 5, 10, 20]
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(4, 2, i + 1)
parameters = nn_model(X, Y, n_h, num_iterations=5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
plt.title("Accuracy for hidden layer size {}, dataset rosedosventor: {}%".format(n_h, accuracy))
plt.show()
其他数据集
def load_extra_datasets():
N = 200
noisy_circles = sklearn.datasets.make_circles(n_samples=N, factor=.5, noise=.3)
noisy_moons = sklearn.datasets.make_moons(n_samples=N, noise=.2)
blobs = sklearn.datasets.make_blobs(n_samples=N, random_state=5, n_features=2, centers=6)
gaussian_quantiles = sklearn.datasets.make_gaussian_quantiles(
mean=None, cov=0.5, n_samples=N, n_features=2, n_classes=2, shuffle=True, random_state=None)
no_structure = np.random.rand(N, 2), np.random.rand(N, 2)
return noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure
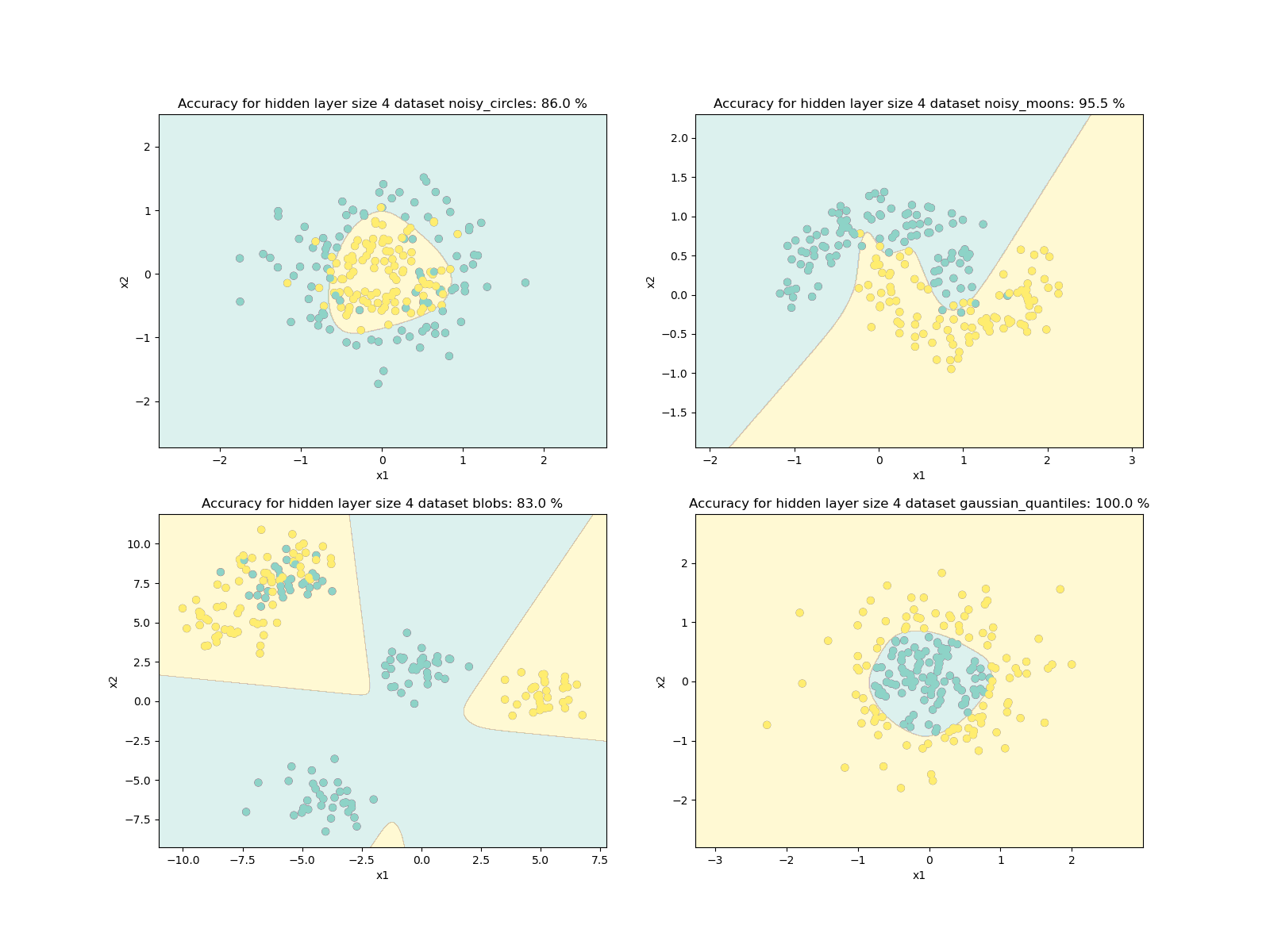
def main():
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
datasets = {"noisy_circles": noisy_circles,
"noisy_moons": noisy_moons,
"blobs": blobs,
"gaussian_quantiles": gaussian_quantiles}
datasetLabels = ["noisy_circles", "noisy_moons", "blobs", "gaussian_quantiles"]
plt.figure(figsize=(16, 12))
for i, dataset in enumerate(datasetLabels):
X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])
if dataset == "blobs":
Y = Y % 2
plt.subplot(2, 2, i + 1)
plt.scatter(X[0, :], X[1, :], c=Y.reshape(X[0, :].shape), s=40, cmap=plt.cm.Spectral)
parameters = nn_model(X, Y, 4)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Accuracy for hidden layer size 4 dataset {}: {} %".format(dataset, accuracy))
plt.show()
关于 Python
plt
plt.scatter：
matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, hold=None, data=None, **kwargs)
- 绘制散点图。
x、y：散点的坐标。s：散点的面积。c：散点的颜色（默认值为蓝色，'b'，其余颜色同plt.plot( )）。marker：散点样式（默认值为实心圆，'o'，其余样式同plt.plot( )）。alpha：散点透明度（[0, 1]之间的数，0 表示完全透明，1 则表示完全不透明）。linewidths：散点的边缘线宽。edgecolors：散点的边缘颜色。cmap：调色盘，取值为plt.cm.Spectral时，给不同c的取值不同的颜色，为不同类别的样本分别分配不同的颜色，但是这个样子不好看，嘻嘻～。- 剩下的参数，以后再探索吧，咕咕咕～
plt.contourf：
- 绘制轮廓线（等高线），对等高线间的填充区域进行填充。
plt.subplot：
- 第一个参数为子图行数，第二个参数为子图列数。第三个参数为索引。
- 子图将分布在行列的索引位置上，索引从 1 开始，从右上角增加到右下角。
np
np.linspace：
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)
- 创建等差数列。
start：返回样本数据开始点。stop：返回样本数据结束点。num：生成的样本数据量，默认为 50。endpoint：True则包含stop；False则不包含stop。retstep：如果为True则结果会给出数据间隔。dtype：输出数组类型。axis：0（默认）或 -1。
np.c_：
- 将将一维数组作为列放入到二维数组中。
np.arrange
- 返回一个有终点和起点的固定步长的排列，如 [1, 2, 3, 4, 5]，起点是 1，终点是 6，步长为 1。
np.meshgrid：
X, Y = np.meshgrid(x, y)
- 将
x中每一个数据和y中每一个数据组合生成很多点，然后将这些点的x坐标放入到X中，y坐标放入Y中，并且相应位置是对应的。
xx.ravel()：
array类型对象的方法，ravel函数将多维数组降为一维，仍返回array数组，元素以列排列。
sklearn
- 咕咕咕～
