应用题3

这道题知识点参考书116页二叉树遍历相关知识。
知识点:
-
二叉树中序遍历,后序遍历的顺序是什么
-
如何将一棵二叉树转化为树(或森林)
-
中序遍历(左->根->右)
-
后序遍历(左->右->根)
根据中序遍历和后序遍历的特点,我们可以知道,中序遍历中根节点在中间,后序遍历中根节点在后面,而作为第一层的根节点会出现在后序序列的最后一个。
- 所以根据题干给出的后序序列我们可以知道第一层的根节点为A。
- 在中序序列中圈住A,左边的就是A的左子树,右边的就是A的右子树。
- 根据上一步已知的左右子树的节点字母,可以在后序序列中也找到左右子树的分界线,分别在左右子树后序序列中最后的一个节点就是左右子树的根,即得到左子树根节点为B,右子树根节点为C。
此后步骤同理,即通过后序序列找根节点,通过中序序列确定左右子树的节点字母,再回到后序序列进行比对。
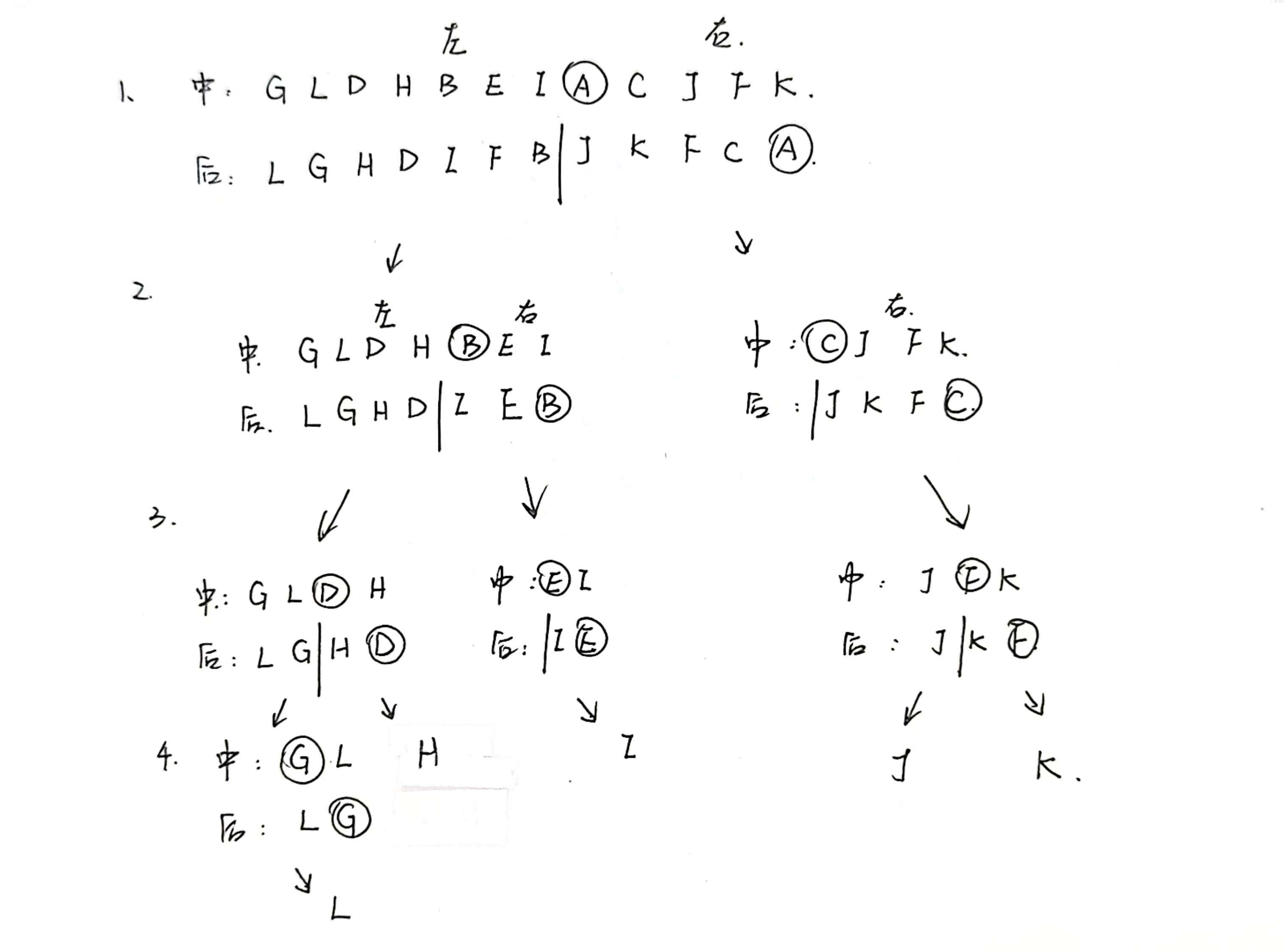
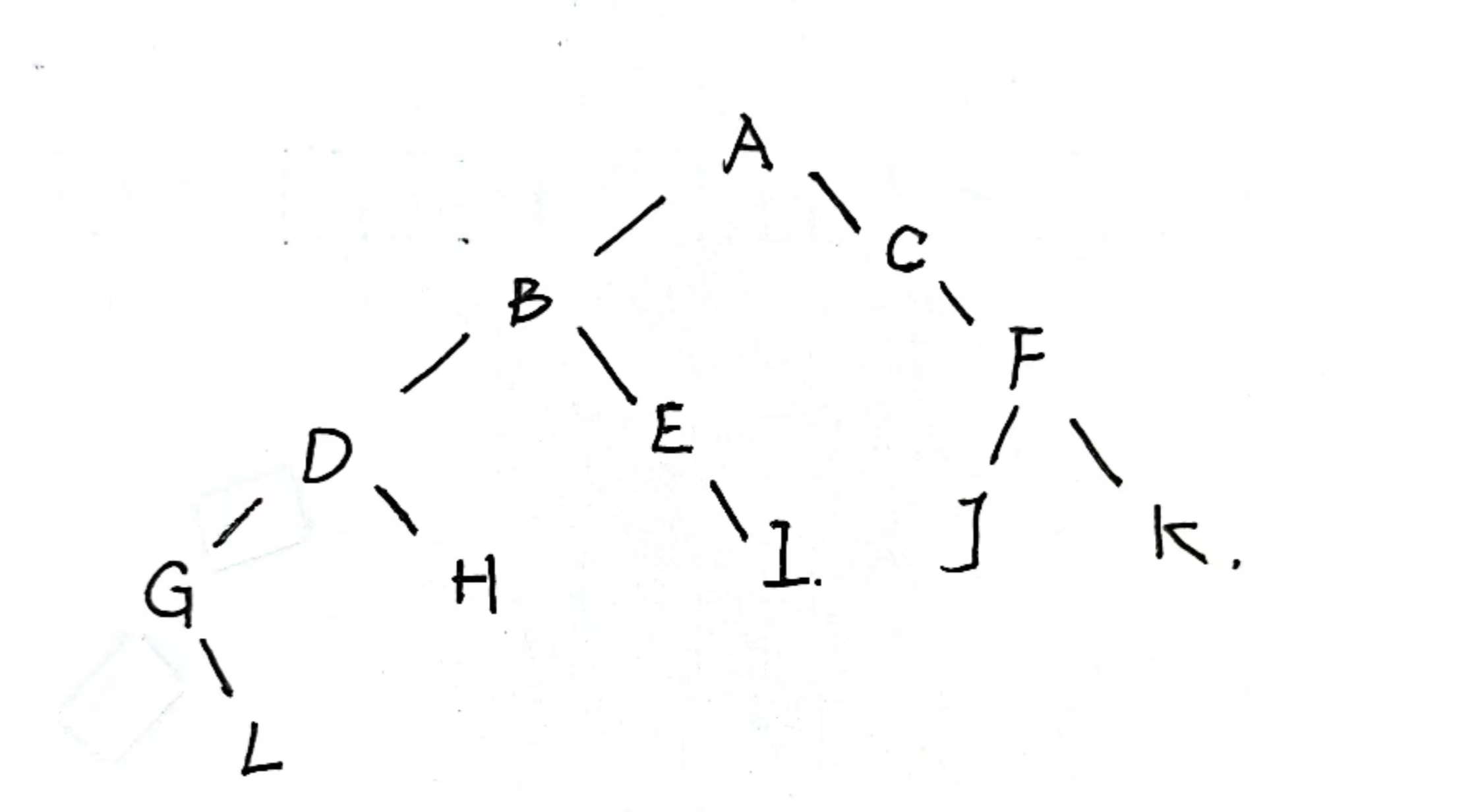
得到答案二叉树
- 二叉树和树,森林的转换
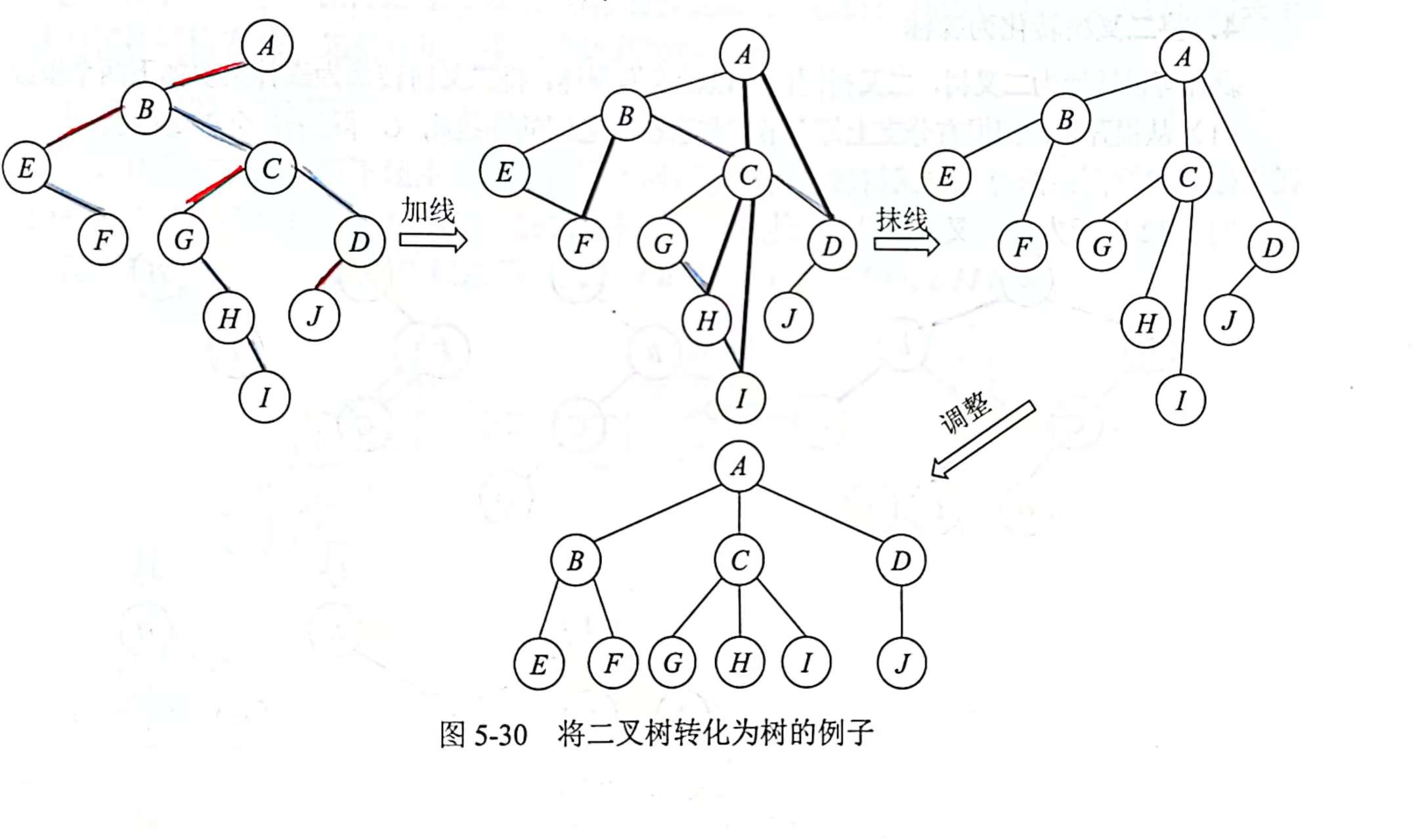
- 二叉树转化为树
(连线)一节点P如果有左孩子,就将该左孩子的右孩子,左孩子右孩子的右孩子...与节点P相连。
(抹线)将被连线的右孩子与双亲的连线擦除
(调整)调整成树的结构
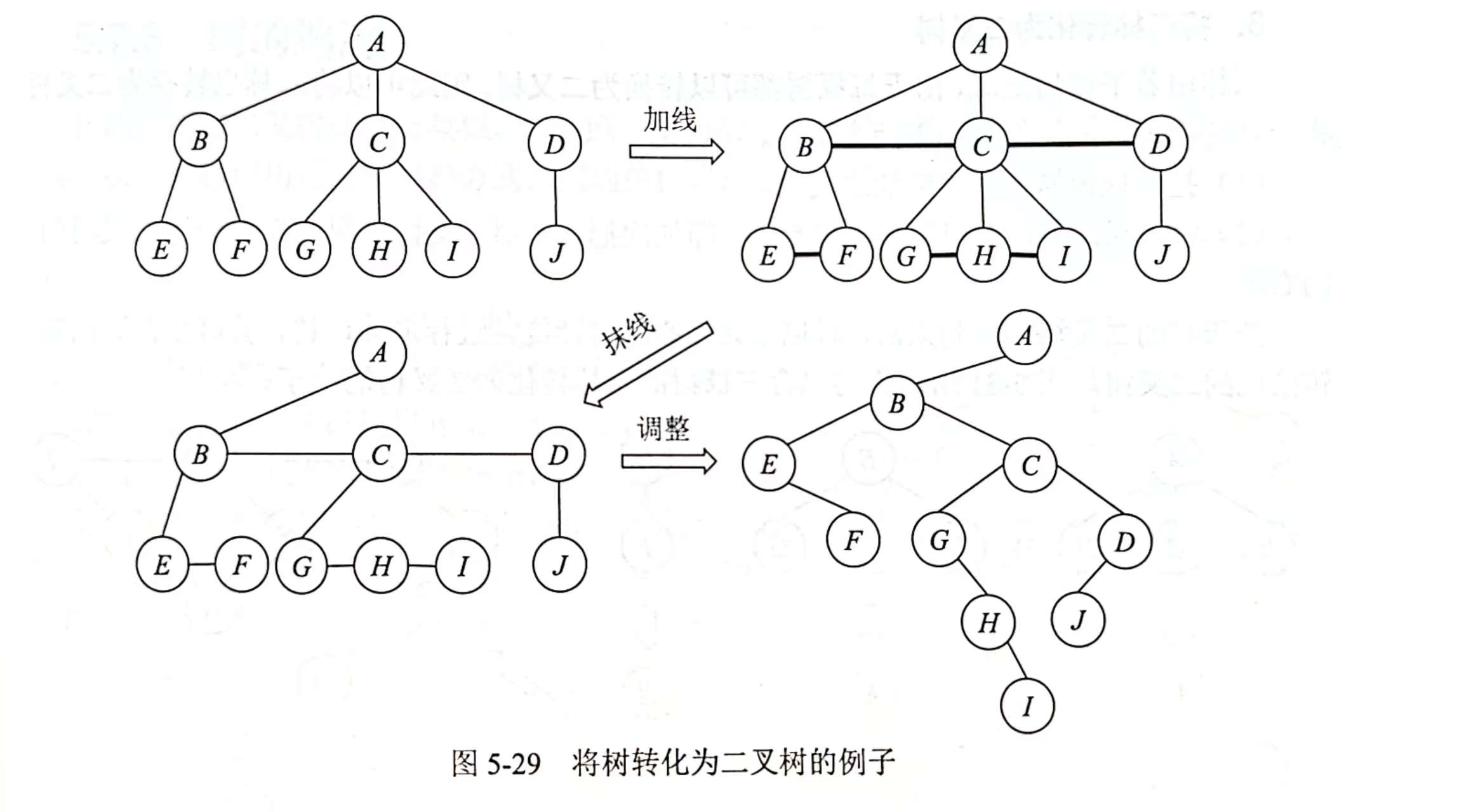
2.树转化为二叉树
(连线)兄弟连线
(抹线)只保留双亲和最大的孩子之间的连线,其他的擦除
(调整)调整成二叉树的结构
3.二叉树转化为森林
首先明确一点,森林由若干棵树构成
(抹线)从根节点开始,将根右分支上每个节点与右孩子的连线擦除
(调整)将每棵分离后得到的二叉树转换为树的结构
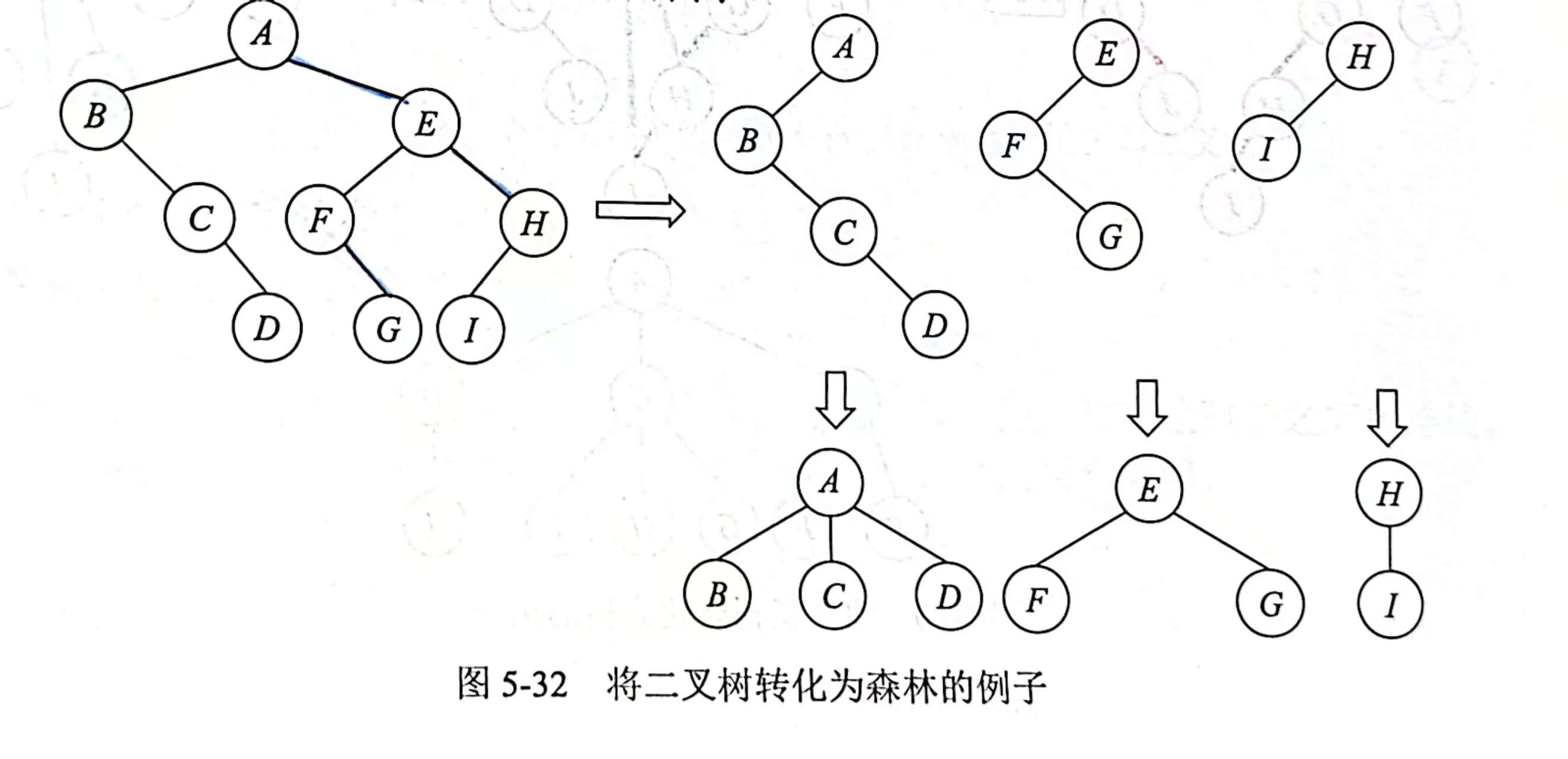
4.森林转化为二叉树
(树转化为二叉树)
(连线)将每棵二叉树的根节点连起来,再依次把后一棵二叉树的根调整为前一棵树的右孩子,再进行结构的调整
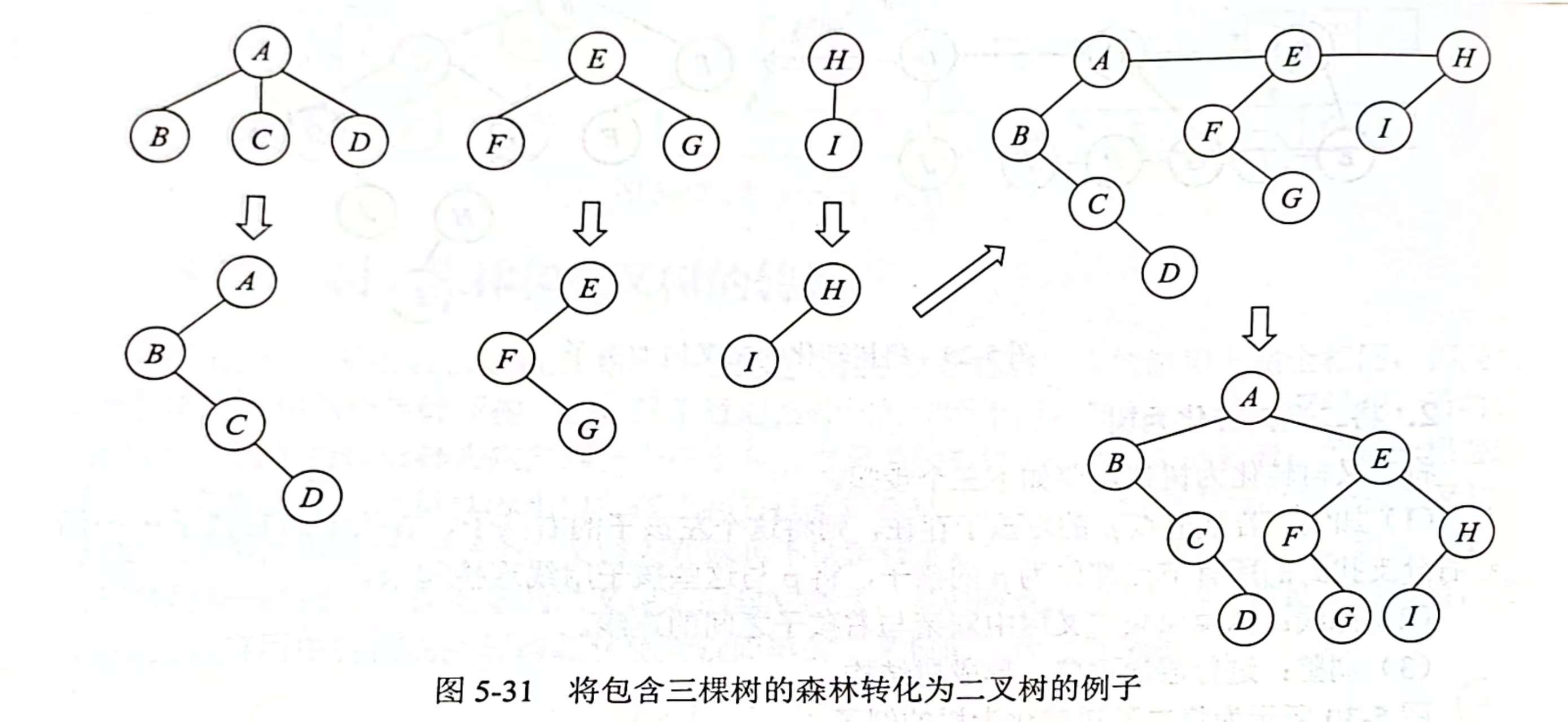
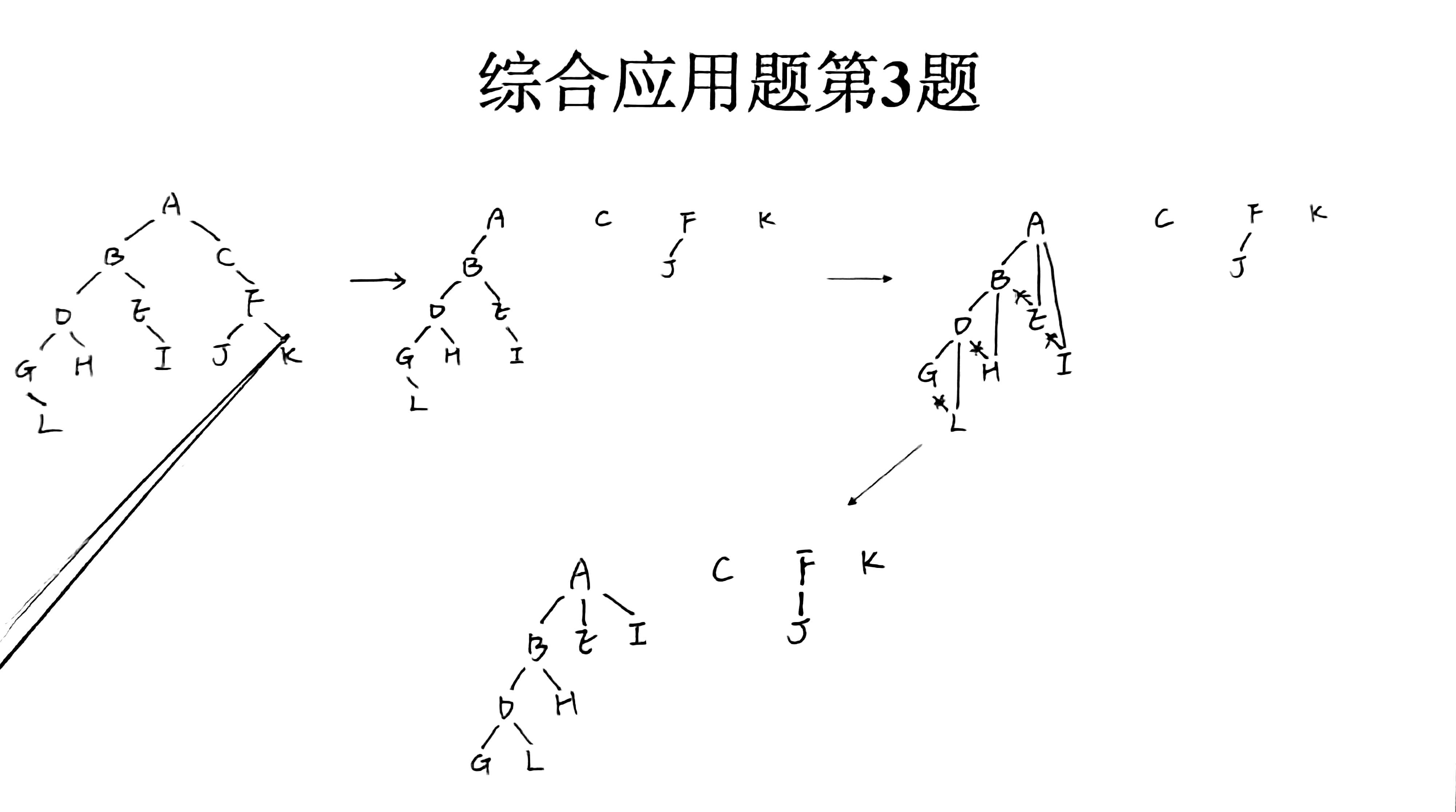
这道题是将二叉树转化成树或森林
判断条件是这个二叉树有没有右孩子




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步