应用题1

这道题知识点参考书97页-100页稀疏矩阵的相关知识。
知识点：

• 什么是稀疏矩阵，三元组线性表和十字链表。
• 什么是转置（运算）。

如果一个矩阵中绝大多数元素数值为0，我们称其为稀疏矩阵
一般稀疏矩阵有两种表示方法，三元组线性表和十字链表

• 三元组线性表：
  我们先来讲讲三元组线性表是如何表示稀疏矩阵的
  举个例子，这里有个稀疏矩阵，长这个样子
  
  矩阵中零太多了，如果每个元素都存储就太占用存储空间了，就这么几个数（分布无规律），我们记一下非零元素的行数，列数和数值就可以了，所以三元组表示法中的三元就分别是行数row,列数col和元素数值value（row,col,value)。如果使用顺序存储结构来存储稀疏矩阵的三元组，可以得到稀疏矩阵的一种压缩存储表达方式--三元组顺序表。
  所以，图中第0行第4列的元素1就表示为（0，4，1）
  如果以行为主序存储，这个稀疏矩阵的三元组顺序表则表示为
  （0，4，1），（2，1，-1），（3，4，-2），（4，0，5），（5，2，7）

• 十字链表法：
  再来说说十字链表法，当矩阵进行运算后，元素数值常常发生较大改动，如果要对元素数值进行删除，插入，修改等工作再用顺序存储会很不方便，所以十字链表法诞生了。
  首先对矩阵的每行每列都分别创建一个不带头节点的单链表。每个非零元素都对应一个节点，因为该节点同时存在与它所在的行链表和列链表中，所以两个链表在此节点形成交叉。为了管理链表，用rowhead数组存储行链表头指针，用colhead数组存储列链表头指针，每个节点对应一个非零元素，存储该非零元素的三元组（row,col,value)以及该节点的行后继指针和列后继指针。
  具体案例：
  

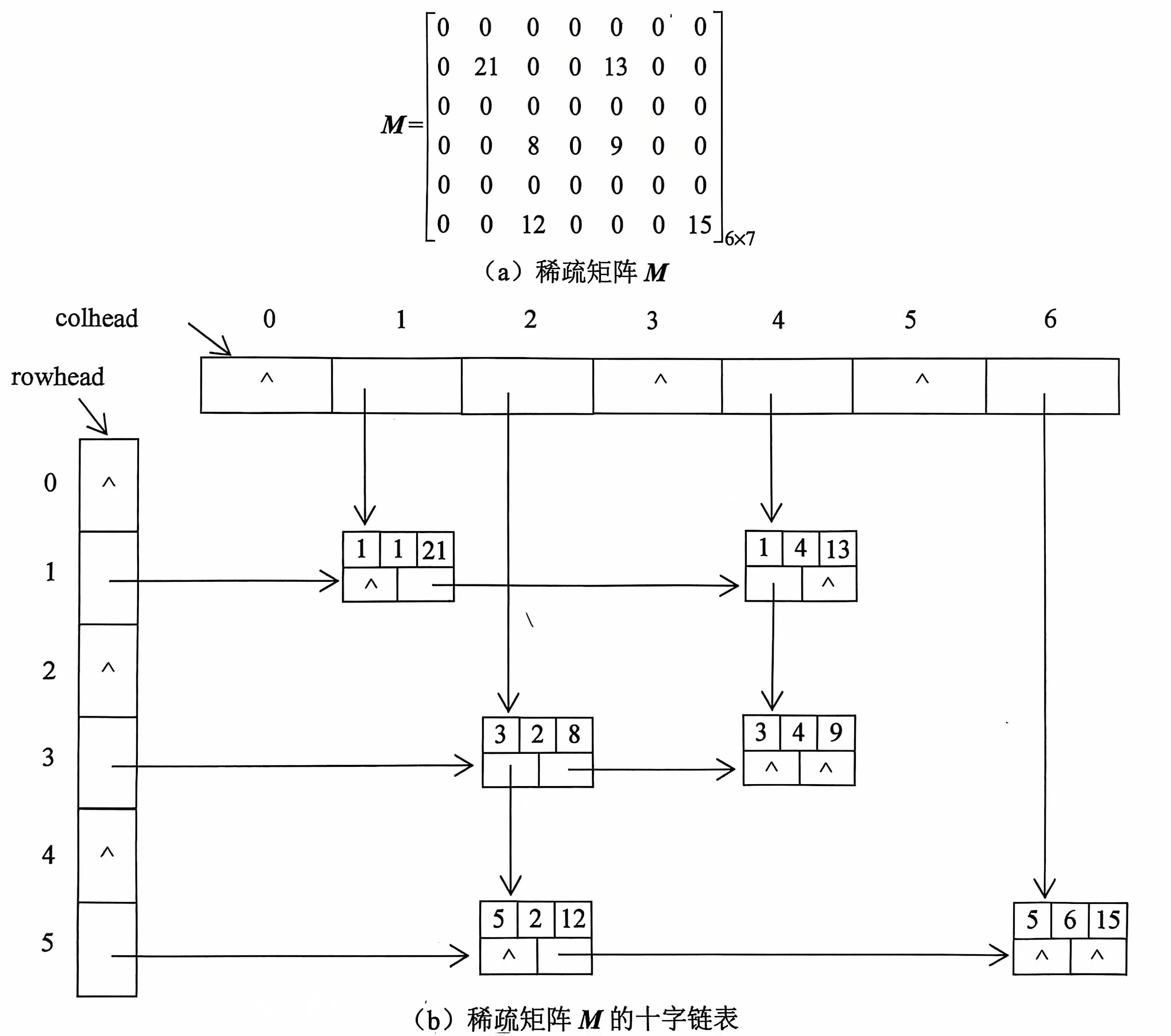
• 转置：大家之前学过线性代数吧，我们知道矩阵有很多运算加法，减法等。题干中提到的转置也是一种我们之前学过的矩阵运算。
  转置矩阵的实现就是将原有矩阵M进行行元素和列元素的调换，使得得到的转置矩阵N（j,i)=M(i,j)
  

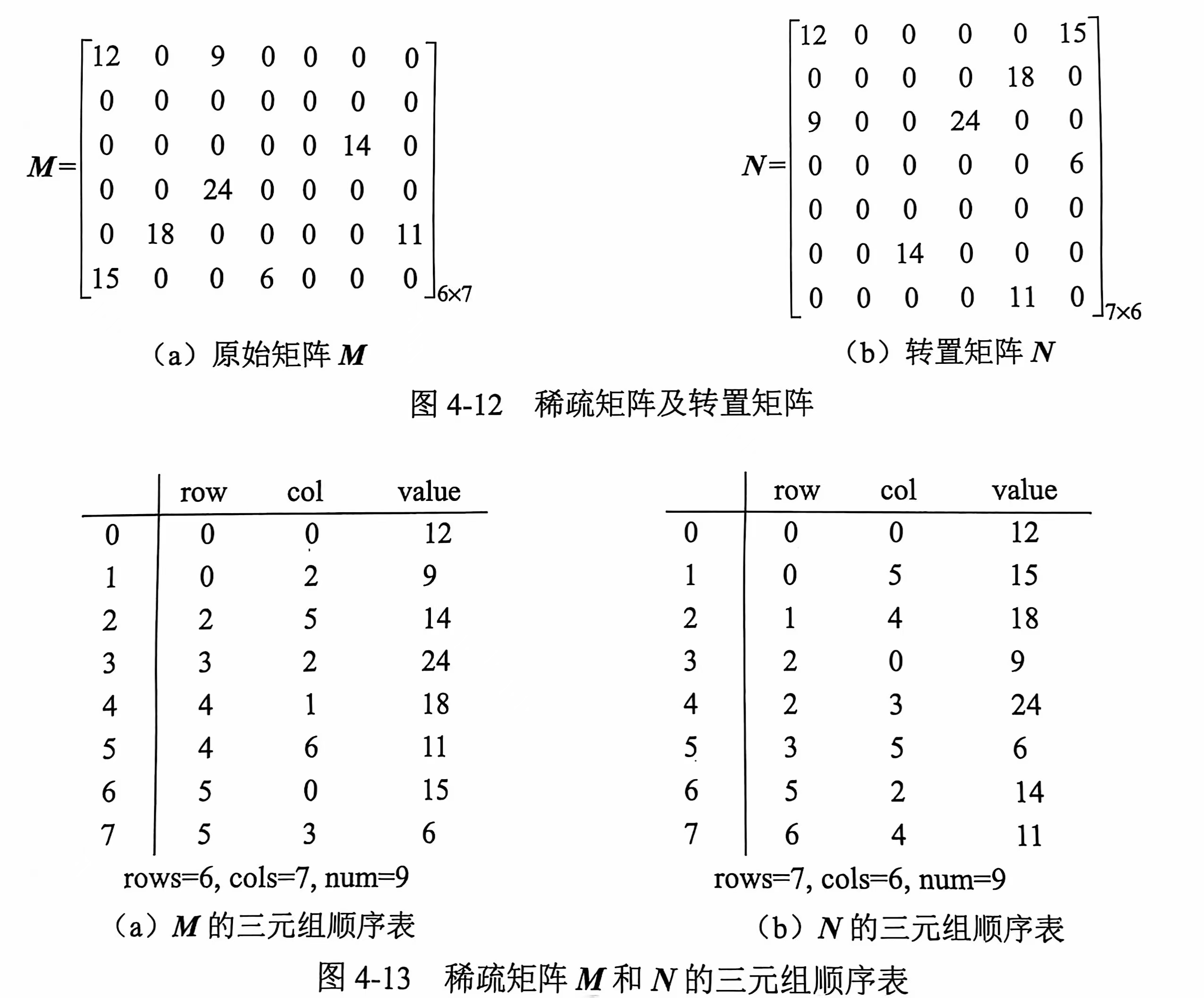
以上就是这道题的全部知识点了。

了解完考点这道题目就很好写了
1.根据给出的三元组线性表画出稀疏矩阵M

2.画出M的十字链表

3.转置M得到N
（其实可以省去这一步，直接将M的非零元素行列交换，再按照顺序重新排列即可）
写出N的三元组线性表