三维重建笔记——稀疏重建
本篇和下篇为2020第三届“SLAM技术及应用”暑期学校申抒含老师讲解的基于图像的三维重建。

后续补充:摸底考试的第一题就可用上述的两种方法解决。题目如下:
1、用一个相机在不同位置拍摄同一物体,得到一组图像序列,
1)请设计一种算法,得到该物体三维重建的结果,并给出详细的算法流程; 2)给出算法流程中用到的重要公式。
题设是不同位置拍摄的图像序列,个人认为用SfM更好,因为它多用来解决离散的图像。

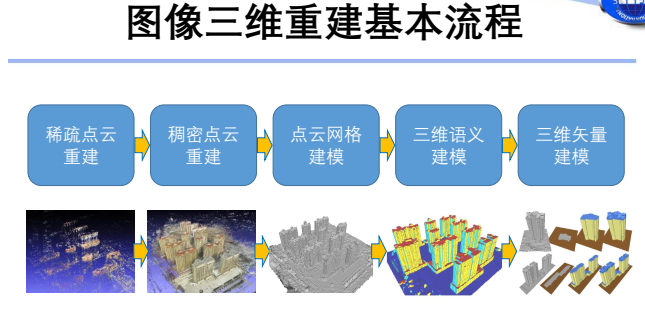
稀疏点云重建
输入:多视角图像
输出:相机位姿、稀疏点云
基础知识
小孔相机模型
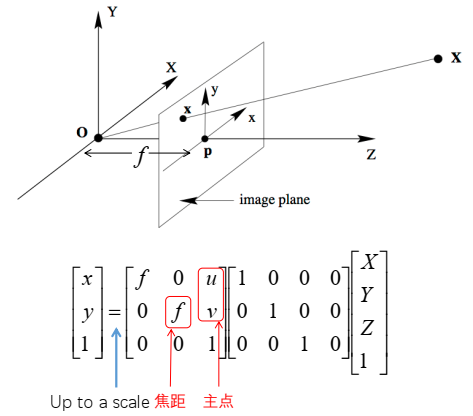
三维点定位在相机坐标系下,并不是常用的,因为相机移动,三维坐标的点也会随之移动。
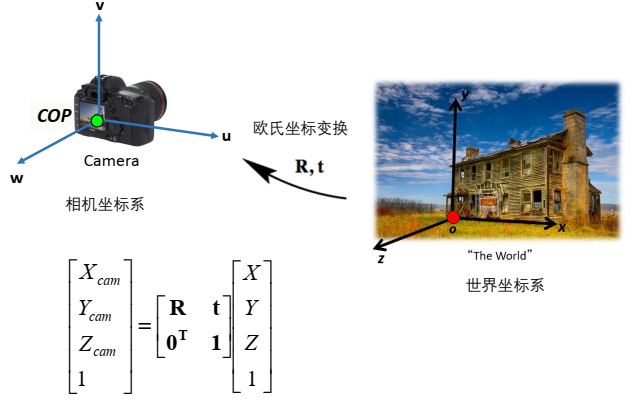
将世界坐标系定义在物体上
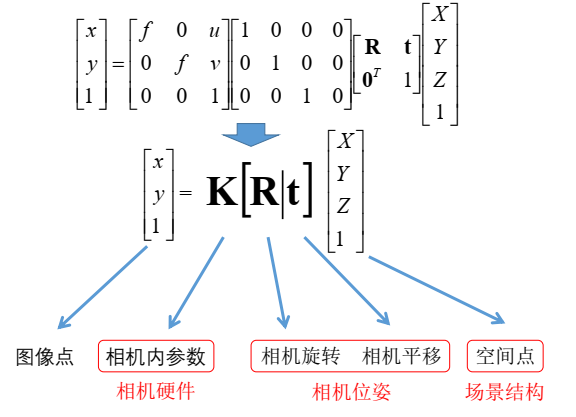
重投影误差最小化
假设已知相机参数K、R、T,已知三维点,那该三维点就能依据小孔相机成像模型投影到图像上。若投影点和实际图像上的二维点他们的图像像素距离尽量的小,那重建结果就比较好。
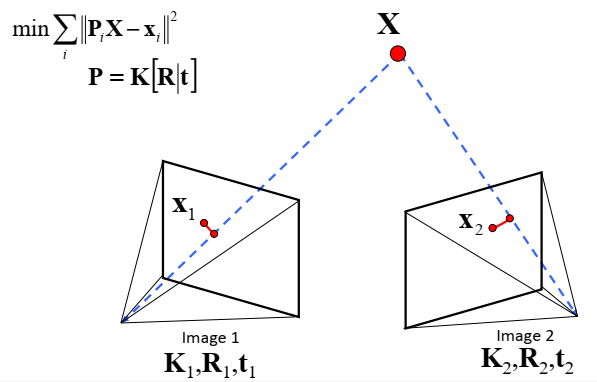

分层重建
主要刻画从两幅视图中如何构建两相机的内外参数以及对应的三维点,为捆绑调整提供有效的初始值。
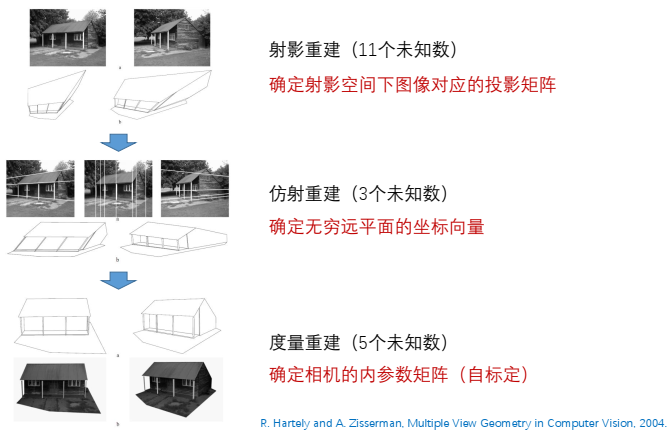
将分层重建拆解成三个子问题,未知数的数量大大减少。
直接度量重建(已知K)
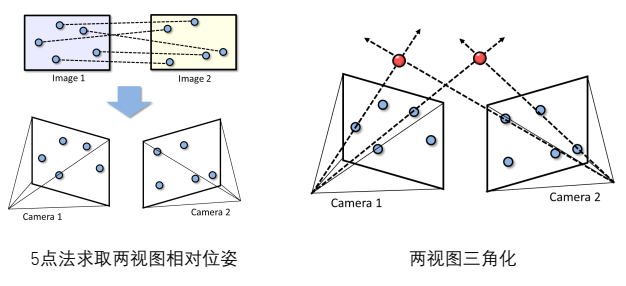
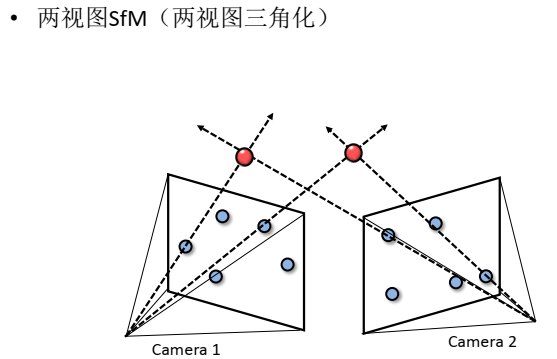
两视图的五个对应点就能解析地求出两相机的R、T。
则两相机的位姿已知,内外参数已知就可通过两视图三角化将所有的三维点求解出来,就可进行捆绑调整。
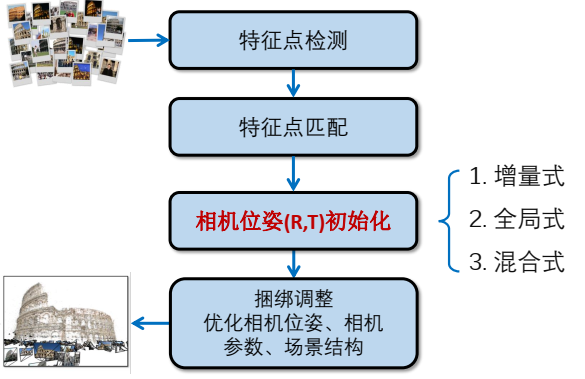
上面解决了两视图的问题,若是几幅图或是成百上千幅,这时如何提供初值,这就是稀疏重建解决的问题。无论什么稀疏重建算法都是在完成所有相机位姿初始化计算的问题。
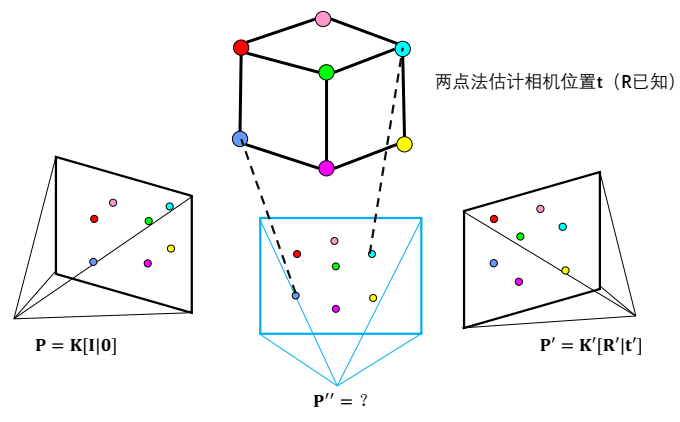
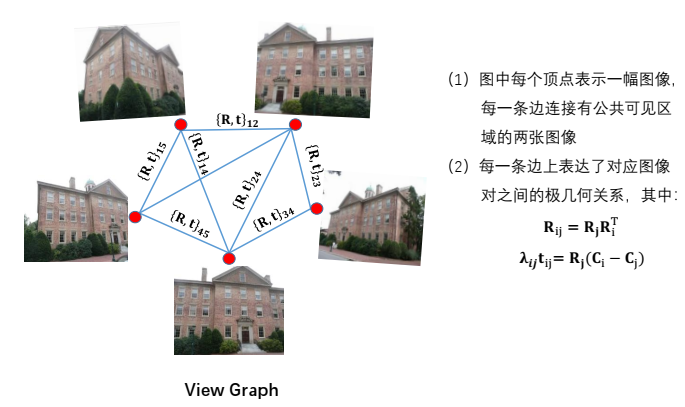
由于SfM因为它的离散特性,输入的不是原始图像,而是图像之间的匹配关系,即view graph(外极几何图)
两个节点的边包含了两幅图像间的特征匹配点,以及在内参数已知时通过五点法分解出的两相机的相对旋转和相对平移。
注:对相机的绝对位置来说,分解出的Tij是一个向量,还有一个未知因子𝛌𝒊𝒋
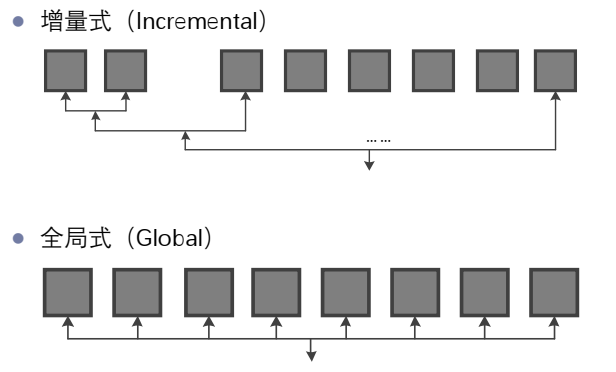
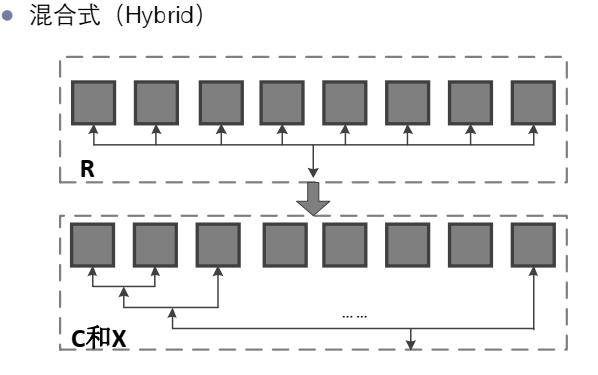

添加第三个相机,在当前的三维点中,选择一幅能够看到当前已重建三维点最多的图像,得到二维图像点和三维点之间的匹配关系。就可以使用多视几何中P3P P4P P5P来计算相机的位姿,这个计算过程也就是相机定位的过程。进而得到三个相机。再进行三角化、调用捆绑调整。不断添加相机、三角化、捆绑调整,得到重建结果。
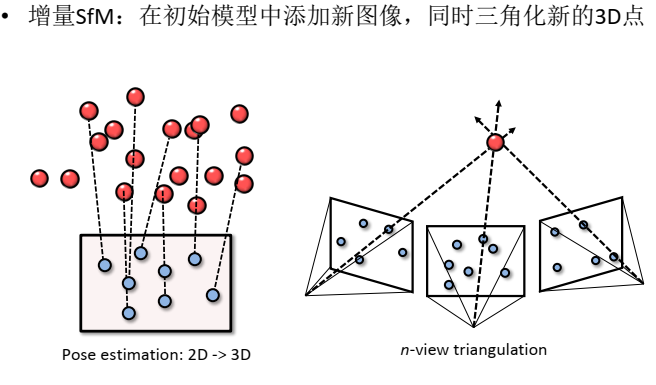

希望一次性估计出所有相机的旋转矩阵、所有相机的绝对位置,这时只要进行三角化,进行一次全局捆绑调整就可以了。
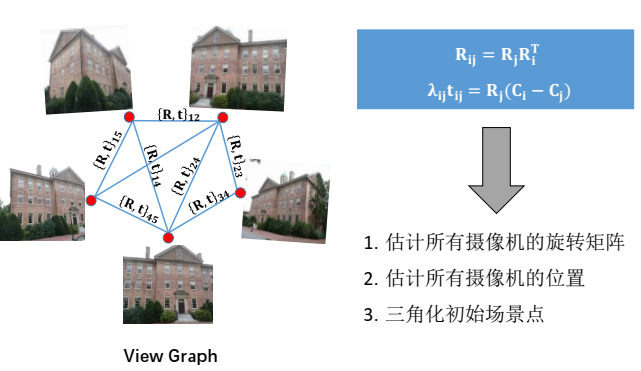
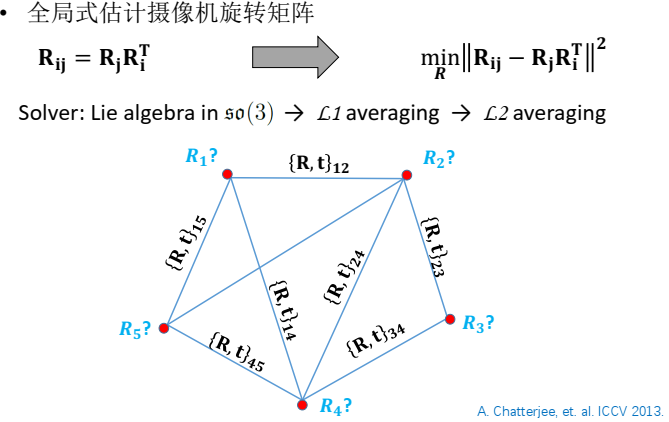
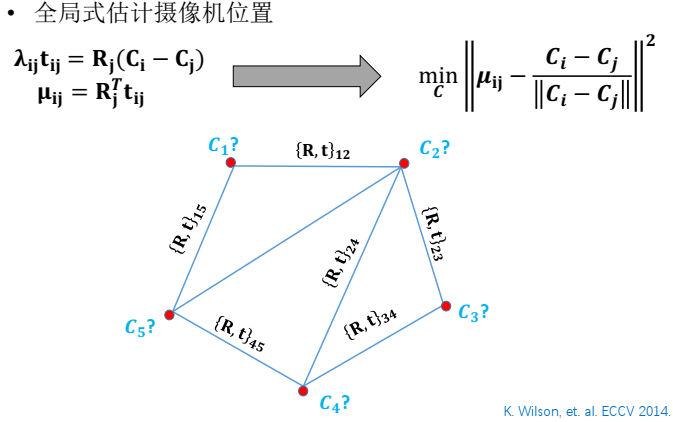
上面的计算相对复杂,主要原因在于通过五点法分解出的两相机的相对平移,只有朝向没有尺度,也就是 𝐭𝐢𝐣是一个向量,还有一个未知的尺度 𝛌𝒊𝒋,要解绝对位置𝐂𝐢 、 𝐂𝐣,𝛌𝒊𝒋很干扰不容易求解。绝大多数的平移平均算法都是想消除𝛌𝒊𝒋的影响。