二叉搜索树BST

BST的定义

　　在二叉查找(搜索)树中:

若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
任意节点的左、右子树也分别为二叉查找树。
没有键值相等的节点。
若对它进行中序遍历，则是一个递增的排好序的序列

作用：

　　用来进行搜索

二叉搜索树注意事项：

　　进行中序遍历，可以得到一个有序的序列
树中最左侧节点一定是最小的节点，最右侧节点一定是最大的

二叉搜索树的实现

节点

public class BSTree<T extends Comparable<T>> {

    private BSTNode<T> mRoot;    // 根结点

    public class BSTNode<T extends Comparable<T>> {
        T key;                // 关键字(键值)
        BSTNode<T> left;      // 左孩子
        BSTNode<T> right;     // 右孩子
        BSTNode<T> parent;    // 父结点

        public BSTNode(T key, BSTNode<T> parent, BSTNode<T> left, BSTNode<T> right) {
            this.key = key;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }
    }

        ......
}

遍历

遍历包含前序遍历、中序遍历、后序遍历3种方式。

¶前序遍历

若二叉树非空，则执行以下操作:

访问根结点；
先序遍历左子树；
先序遍历右子树。

private void preOrder(BSTNode<T> tree) {
    if(tree != null) {
        System.out.print(tree.key+" ");
        preOrder(tree.left);
        preOrder(tree.right);
    }
}

public void preOrder() {
    preOrder(mRoot);
}

中序遍历

若二叉树非空，则执行以下操作:

中序遍历左子树；
访问根结点；
中序遍历右子树。

private void inOrder(BSTNode<T> tree) {
    if(tree != null) {
        inOrder(tree.left);
        System.out.print(tree.key+" ");
        inOrder(tree.right);
    }
}

public void inOrder() {
    inOrder(mRoot);
}

后序遍历

若二叉树非空，则执行以下操作:

后序遍历左子树；
后序遍历右子树；
访问根结点。

private void postOrder(BSTNode<T> tree) {
    if(tree != null)
    {
        postOrder(tree.left);
        postOrder(tree.right);
        System.out.print(tree.key+" ");
    }
}

public void postOrder() {
    postOrder(mRoot);
}

------------------------------------------------此处为分割线(#^.^#)------------------------------------------------

下面这颗树的各种遍历方式:

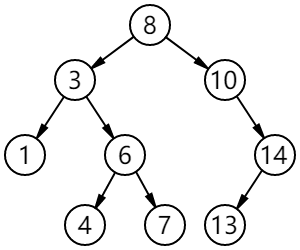
对于上面的二叉树而言，

前序遍历结果: 8 3 1 6 4 7 10 14 13
中序遍历结果: 1 3 4 6 7 8 10 13 14
后序遍历结果: 1 4 7 6 3 13 14 10 8

取最大值和最小值

/* 
 * 查找最大结点: 返回tree为根结点的二叉树的最大结点。
 */
private BSTNode<T> maximum(BSTNode<T> tree) {
    if (tree == null)
        return null;

    while(tree.right != null)
        tree = tree.right;
    return tree;
}

public T maximum() {
    BSTNode<T> p = maximum(mRoot);
    if (p != null)
        return p.key;

    return null;
}

/* 
 * 查找最小结点: 返回tree为根结点的二叉树的最小结点。
 */
private BSTNode<T> minimum(BSTNode<T> tree) {
    if (tree == null)
        return null;

    while(tree.left != null)
        tree = tree.left;
    return tree;
}

public T minimum() {
    BSTNode<T> p = minimum(mRoot);
    if (p != null)
        return p.key;

    return null;
}

查找

/*
 * (递归实现)查找"二叉树x"中键值为key的节点
 */
private BSTNode<T> search(BSTNode<T> x, T key) {
    if (x==null)
        return x;

    int cmp = key.compareTo(x.key);
    if (cmp < 0)
        return search(x.left, key);
    else if (cmp > 0)
        return search(x.right, key);
    else
        return x;
}

public BSTNode<T> search(T key) {
    return search(mRoot, key);
}

前驱和后继

节点的前驱: 是该节点的左子树中的最大节点。节点的后继: 是该节点的右子树中的最小节点。

取得前驱结点：

/* 
 * 找结点(x)的前驱结点。即，查找"二叉树中数据值小于该结点"的"最大结点"。
 */
public BSTNode<T> predecessor(BSTNode<T> x) {
    // 如果x存在左孩子，则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
    if (x.left != null)
        return maximum(x.left);

    // 如果x没有左孩子。则x有以下两种可能: 
    // (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
    // (01) x是"一个左孩子"，则查找"x的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"。
    BSTNode<T> y = x.parent;
    while ((y!=null) && (x==y.left)) {
        x = y;
        y = y.parent;
    }

    return y;
}

取得后继节点

/* 
 * 找结点(x)的后继结点。即，查找"二叉树中数据值大于该结点"的"最小结点"。
 */
public BSTNode<T> successor(BSTNode<T> x) {
    // 如果x存在右孩子，则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
    if (x.right != null)
        return minimum(x.right);

    // 如果x没有右孩子。则x有以下两种可能: 
    // (01) x是"一个左孩子"，则"x的后继结点"为 "它的父结点"。
    // (02) x是"一个右孩子"，则查找"x的最低的父结点，并且该父结点要具有左孩子"，找到的这个"最低的父结点"就是"x的后继结点"。
    BSTNode<T> y = x.parent;
    while ((y!=null) && (x==y.right)) {
        x = y;
        y = y.parent;
    }

    return y;
}

插入新节点

/* 
 * 将结点插入到二叉树中
 *
 * 参数说明: 
 *     tree 二叉树的
 *     z 插入的结点
 */
private void insert(BSTree<T> bst, BSTNode<T> z) {
    int cmp;
    BSTNode<T> y = null;
    BSTNode<T> x = bst.mRoot;

    // 查找z的插入位置
    while (x != null) {
        y = x;
        cmp = z.key.compareTo(x.key);
        if (cmp < 0)
            x = x.left;
        else
            x = x.right;
    }

    z.parent = y;
    if (y==null)
        bst.mRoot = z;
    else {
        cmp = z.key.compareTo(y.key);
        if (cmp < 0)
            y.left = z;
        else
            y.right = z;
    }
}

/* 
 * 新建结点(key)，并将其插入到二叉树中
 *
 * 参数说明: 
 *     tree 二叉树的根结点
 *     key 插入结点的键值
 */
public void insert(T key) {
    BSTNode<T> z=new BSTNode<T>(key,null,null,null);

    // 如果新建结点失败，则返回。
    if (z != null)
        insert(this, z);
}

删除节点

/* 
 * 删除结点(z)，并返回被删除的结点
 *
 * 参数说明: 
 *     bst 二叉树
 *     z 删除的结点
 */
private BSTNode<T> remove(BSTree<T> bst, BSTNode<T> z) {
    BSTNode<T> x=null;
    BSTNode<T> y=null;

    if ((z.left == null) || (z.right == null) )
        y = z;
    else
        y = successor(z);

    if (y.left != null)
        x = y.left;
    else
        x = y.right;

    if (x != null)
        x.parent = y.parent;

    if (y.parent == null)
        bst.mRoot = x;
    else if (y == y.parent.left)
        y.parent.left = x;
    else
        y.parent.right = x;

    if (y != z) 
        z.key = y.key;

    return y;
}

/* 
 * 删除结点(z)，并返回被删除的结点
 *
 * 参数说明: 
 *     tree 二叉树的根结点
 *     z 删除的结点
 */
public void remove(T key) {
    BSTNode<T> z, node; 

    if ((z = search(mRoot, key)) != null)
        if ( (node = remove(this, z)) != null)
            node = null;
}

打印

/*
 * 打印"二叉查找树"
 *
 * key        -- 节点的键值 
 * direction  --  0，表示该节点是根节点;
 *               -1，表示该节点是它的父结点的左孩子;
 *                1，表示该节点是它的父结点的右孩子。
 */
private void print(BSTNode<T> tree, T key, int direction) {

    if(tree != null) {

        if(direction==0)    // tree是根节点
            System.out.printf("%2d is root\n", tree.key);
        else                // tree是分支节点
            System.out.printf("%2d is %2d's %6s child\n", tree.key, key, direction==1?"right" : "left");

        print(tree.left, tree.key, -1);
        print(tree.right,tree.key,  1);
    }
}

public void print() {
    if (mRoot != null)
        print(mRoot, mRoot.key, 0);
}

销毁树

/*
 * 销毁二叉树
 */
private void destroy(BSTNode<T> tree) {
    if (tree==null)
        return ;

    if (tree.left != null)
        destroy(tree.left);
    if (tree.right != null)
        destroy(tree.right);

    tree=null;
}

public void clear() {
    destroy(mRoot);
    mRoot = null;
}

代码实现

package Tree.BSTree;

public class BSTree<T extends Comparable<T>> {

    private BSTNode<T> mRoot; //根节点

    /**
     * 构建BST
     * @param <T>
     */
    public class BSTNode<T extends Comparable<T>>{
        T key;  //键值
        BSTNode<T> left;
        BSTNode<T> right;
        BSTNode<T> parent;

        public BSTNode(T key, BSTNode<T> parent,BSTNode<T> left, BSTNode<T> right){
            this.key = key;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }

        public T getKey(){
            return key;
        }

        public String toString(){
            return "key:" + key;
        }
    }

    public BSTree(){
        mRoot = null;
    }

    /**
     * 前序遍历
     */
      private void preOrder(BSTNode<T> tree){
          if(tree != null){
              System.out.print(tree.key + " ");
              preOrder(tree.left);
              preOrder(tree.right);
          }
      }

      public void preOrder(){
          preOrder(mRoot);
      }
    /**
     * 中序遍历
     */
      private void inOrder(BSTNode<T> tree){
          if(tree != null){
              inOrder(tree.left);
              System.out.print(tree.key + " ");
              inOrder(tree.right);
          }
      }
      public void inOrder(){
          inOrder(mRoot);
      }
    /**
     * 后序遍历
     */
    private void postOrder(BSTNode<T> tree){
        if(tree != null){
            postOrder(tree.left);
            postOrder(tree.right);
            System.out.print(tree.key+" ");
        }
    }

    public void postOrder(){
        postOrder(mRoot);
    }


    /*
     * (递归实现)查找"二叉树x"中键值为key的节点
     */
    private BSTNode<T> search(BSTNode<T> x, T key) {
        if (x==null)
            return x;

        int cmp = key.compareTo(x.key);
        if (cmp < 0)
            return search(x.left, key);
        else if (cmp > 0)
            return search(x.right, key);
        else
            return x;
    }

    public BSTNode<T> search(T key) {
        return search(mRoot, key);
    }

    /*
     * (非递归实现)查找"二叉树x"中键值为key的节点
     */
    private BSTNode<T> iterativeSearch(BSTNode<T> x, T key) {
        while (x!=null) {
            int cmp = key.compareTo(x.key);

            if (cmp < 0)
                x = x.left;
            else if (cmp > 0)
                x = x.right;
            else
                return x;
        }

        return x;
    }

    public BSTNode<T> iterativeSearch(T key) {
        return iterativeSearch(mRoot, key);
    }
    /**
     * 查找最大节点
     */
     private BSTNode<T> maximum(BSTNode<T> tree){
         if(tree == null)
             return null;
         while (tree.right != null)
             tree = tree.right;
         return  tree;
     }
     public T maximum(){
         BSTNode<T> p = maximum(mRoot);
         if(p != null)
             return p.key;

         return  null;
     }
    /**
     * 查找最小节点
     */
    private BSTNode<T> minimum(BSTNode<T> tree){
        if(tree == null)
            return null;

        while (tree.left != null)
            tree = tree.left;
        return tree;
    }
    public T minimum(){
        BSTNode<T> p = minimum(mRoot);
        if(p != null)
            return p.key;
        return null;
    }
    /**
     * 查找前驱
     */
    public BSTNode<T> predecessor(BSTNode<T> x){
        // 如果x存在左孩子，则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
        if(x.left != null)
            return maximum(x.left);

        // 如果x没有左孩子。则x有以下两种可能:
        // (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
        // (01) x是"一个左孩子"，则查找"x的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"。
        BSTNode<T> y = x.parent;
        while ((y!=null) && (x == y.left)){
            x = y;
            y = y.parent;
        }

        return  y;
    }
    /**
     * 查找后继
     */
    public BSTNode<T> successor(BSTNode<T> x){
        // 如果x存在右孩子，则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
        if(x.right != null)
            return minimum(x.right);

        // 如果x没有右孩子。则x有以下两种可能:
        // (01) x是"一个左孩子"，则"x的后继结点"为 "它的父结点"。
        // (02) x是"一个右孩子"，则查找"x的最低的父结点，并且该父结点要具有左孩子"，找到的这个"最低的父结点"就是"x的后继结点"。
        BSTNode<T> y = x.parent;
        while ((y != null) && (x == y.right)){
            x = y;
            y = y.parent;
        }
        return y;
    }
    /**
     * 二叉树插入节点
     */

    private void insert(BSTree<T> bst,BSTNode<T> z){
        int cmp;
        BSTNode<T> y = null;
        BSTNode<T> x = bst.mRoot;

        //查找z插入的位置
        while(x != null){
            y = x;
            cmp = z.key.compareTo(x.key);
            if (cmp < 0)
                x = x.left;
            else x = x.right;
        }

        z.parent = y;
        if(y == null)
            bst.mRoot = z;
        else{
            cmp = z.key.compareTo(y.key);
            if(cmp < 0)
                y.left = z;
            else y.right = z;
        }
    }

    public void insert(T key){
        BSTNode<T> z = new BSTNode<T>(key,null,null,null);
        //如果新建节点失败，则返回
        if(z != null)
            insert(this,z);
    }

    /**
     * 删除节点
     */
    private BSTNode<T> remove(BSTree<T> bst, BSTNode<T> z){
        BSTNode<T> x = null;
        BSTNode<T> y = null;

        if((z.left == null) || (z.right == null))
            y = z;
        else
            y = successor(z);
        if(y.left != null)
            x = y.left;
        else x = y.right;

        if(x != null)
            x.parent = y.parent;
        if(y.parent == null)
            bst.mRoot = x;
        else if(y == y.parent.left)
            y.parent.left = x;
        else y.parent.right = x;

        if(y != z)
            z.key = y.key;
        return y;
    }

    public void remove(T key){
        BSTNode<T> z,node;

        if((z = search(mRoot,key)) != null)
            if((node = remove(this,z)) != null)
                node  = null;
    }
    /**
     * 打印
     */
    private void print(BSTNode<T> tree,T key,int direction){
        if(tree != null){
            if(direction == 0)
                System.out.printf("%2d is root\n",tree.key);
            else
                System.out.printf("%2d is %2d's %6s child\n",tree.key,key,direction==1?"right":"left");
            print(tree.left, tree.key,-1);
            print(tree.right,tree.key,1);
        }
    }
    public void print(){
        if(mRoot != null)
            print(mRoot,mRoot.key,0);
    }

    /**
     * 销毁二叉树
     */
    private void destory(BSTNode<T> tree){
        if(tree == null)
            return;
        if(tree.left != null)
            destory(tree.left);
        if(tree.right != null)
            destory(tree.right);
        tree = null;
    }

    public void clear(){
        destory(mRoot);
        mRoot = null;
    }
}

测试代码

package Tree.BSTree;

public class BSTreeTest {

    private static final int arr[] = {1,5,4,3,2,6};

    public static void main(String[] args){
        int i,ilen;
        BSTree<Integer> tree = new BSTree<>();

        System.out.print("=== 依次添加:");
        ilen = arr.length;
        for(i=0 ;i<ilen; i++){
            System.out.print(arr[i] + " ");
            tree.insert(arr[i]);
        }

        System.out.print("\n== 前序遍历：");
        tree.preOrder();;

        System.out.print("\n== 中序遍历：");
        tree.inOrder();

        System.out.print("\n== 后序遍历：");
        tree.postOrder();
        System.out.println();

        System.out.println("== 最小值：" + tree.minimum());
        System.out.println("== 最大值：" + tree.maximum());
        System.out.println("== 树的详细信息：");
        tree.print();

        System.out.print("\n== 删除根节点：" + arr[3]);
        tree.remove(arr[3]);

        System.out.print("\n== 中序遍历：");
        tree.inOrder();
        System.out.println();

        //销毁
        tree.clear();
    }
}

posted @ 2021-05-18 15:17 Jesen等不等式阅读(87) 评论(0) 编辑收藏举报

刷新页面返回顶部

Wu_haha

现在摸的鱼，将来是要用命和加倍时间补回来的

二叉搜索树BST

BST的定义

作用：

二叉搜索树注意事项：

二叉搜索树的实现

节点

遍历

¶前序遍历

中序遍历

后序遍历

取最大值和最小值

查找

前驱和后继

插入新节点

删除节点

打印

销毁树

代码实现

测试代码

公告