AVL树的理解及自写AVL树

AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O（log n）。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

节点的平衡因子是它的左子树的高度减去它的右子树的高度（有时相反）。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。

 

AVL树的基本操作一般涉及运作同在不平衡的二叉查找树所运作的同样的算法。但是要进行预先或随后做一次或多次所谓的"AVL旋转"。

以上内容转自维基百科AVL树

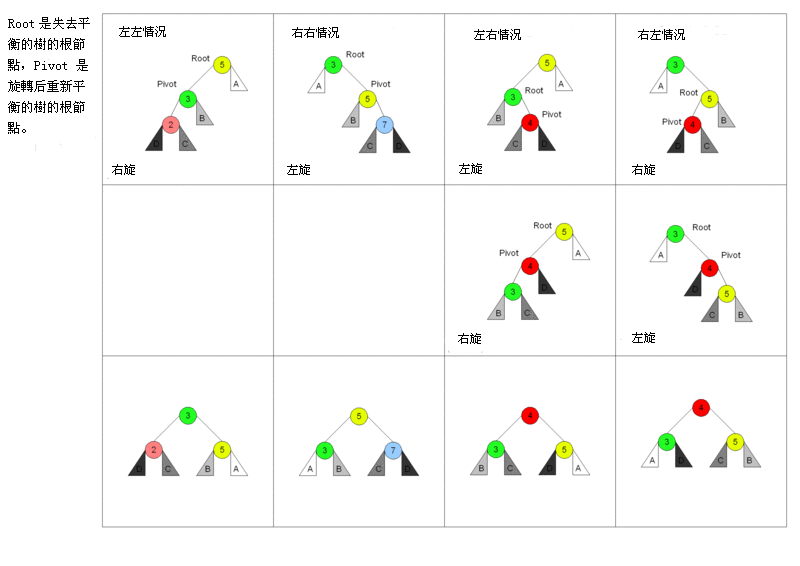
    从图中可以比较形象的看出所谓左旋右旋的旋转支点是三个主节点中大小居中的那个节点，左旋就是左边的节点降下来，右旋就是右边的节点降下来，都成为中间节点的子树。

左右双旋分解就是先将左侧节点降为左子树，右边节点将为右子树。当然中间有合并子树的过程，这里没有细说。

高度为h的AVL树，节点数N最多； 最少 ( 其中 )N是h的斐波那契数列。

 

//定义节点
class AvlNode{
    int val;
    AvlNode left;
    AvlNode right;
    int height;
    public AvlNode(int val,AvlNode left,AvlNode right){
        this.val=val;
        this.left=left;
        this.right=right;
        this.height=0;
    }
    public AvlNode(int val){
        this(val,null,null);
    }
}
public class AVLTree {
    private static final int COUNT=1;
    //判断高度
    private static int height(AvlNode t) {
        // TODO Auto-generated method stub
        return t==null?-1:t.height;
    } 
    //节点的插入
  public  static AvlNode insert(Integer val,AvlNode t){
    
      if(t==null){
        return new AvlNode(val);
      }
      int result=val.compareTo(t.val);
      if(result<0){
          t.left=insert(val, t.left);
      }
      else  if(result>0){
          t.right=insert(val, t.right);
      }else{
          ;
      }
      //其余按照普通的二叉查找树来写，最后加一个平衡方法
      return balance(t);  
  }
  //删除方法，选择了一种比较简单的，在删除之后重新调整树
  public static AvlNode remove(Integer x,AvlNode t){
    if(t==null){
        return null;
    }
    int result=x.compareTo(t.val);
    if(result<0){
        t.left=remove(x, t.left);
    }else if(result>0){
        t.right=remove(x,t.right);
    }
    else if(t.left!=null&&t.right!=null){
        t.val=findMin(t.right).val;
        t.right=remove(t.val,t.right);
    }else{
        t=(t.left!=null)?t.left:t.right;
    }
    return balance(t);  
  }
  
  private static AvlNode findMin(AvlNode t) {
    if(t==null){
        return null;
    }else if(t.left==null){
        return t;
    }
    return findMin(t.left);
}
//平衡方法
   private static AvlNode balance(AvlNode t) {
    // TODO Auto-generated method stub
       //判断是哪种情况
       //如果是左左情况或者是左右情况
     if(height(t.left)-height(t.right)>COUNT){
         if(height(t.left.left)-height(t.right.right)>COUNT){
             //左左情况进行右旋
             t=rightSpin(t);
         }else{
             //右左情况先左旋后右旋
             t=leftrightSpin(t);
         }
      
     }
      //如果是右右情况或者是右左情况
     else if(height(t.right)-height(t.left)>COUNT){
         if(height(t.right.right)-height(t.right.left)>COUNT){
             //右右情况进行左旋
             t=leftSpin(t);
         }else{
             //右左情况先右旋再左旋
             t=rightleftSpin(t);
         }
     }
     return null;
   }
private static AvlNode rightleftSpin(AvlNode t) {
    t.right=rightSpin(t.right);
    return leftSpin(t);
}
private static AvlNode leftrightSpin(AvlNode t) {
    t.left=leftSpin(t.left);
    return rightSpin(t);
}
private static AvlNode leftSpin(AvlNode t) {
    AvlNode t1=t.right;
    t.right=t1.left;
    t1.left=t;
    t1.height=Math.max(height(t1.left), height(t1.right))+1;
    t.height=Math.max(height(t.left),height(t.right));
    return t1;
}
private static AvlNode rightSpin(AvlNode t) {
    AvlNode t1=t.left;
    t.left=t1.right;
    t1.right=t;
    t1.height=Math.max(height(t1.left), height(t1.right))+1;
    t.height=Math.max(height(t.left),height(t.right));
    return t1;
}

}