机器学习之特征工程

一、特征工程概述

       “数据决定了机器学习的上限，而算法只是尽可能逼近这个上限”，这里的数据指的就是经过特征工程得到的数据。特征工程指的是把原始数据转变为模型的训练数据的过程，它的目的就是获取更好的训练数据特征，使得机器学习模型逼近这个上限。特征工程能使得模型的性能得到提升，有时甚至在简单的模型上也能取得不错的效果。特征工程在机器学习中占有非常重要的作用，一般认为括特征构建、特征提取、特征选择三个部分。特征构建比较麻烦，需要一定的经验。 特征提取与特征选择都是为了从原始特征中找出最有效的特征。它们之间的区别是特征提取强调通过特征转换的方式得到一组具有明显物理或统计意义的特征；而特征选择是从特征集合中挑选一组具有明显物理或统计意义的特征子集。两者都能帮助减少特征的维度、数据冗余，特征提取有时能发现更有意义的特征属性，特征选择的过程经常能表示出每个特征的重要性对于模型构建的重要性。本文主要尝试总结几个常用的特征提取和特征选择的方法。

二、特征构建

       特征构建是指从原始数据中人工的找出一些具有物理意义的特征。需要花时间去观察原始数据，思考问题的潜在形式和数据结构，对数据敏感性和机器学习实战经验能帮助特征构建。除此之外，属性分割和结合是特征构建时常使用的方法。结构性的表格数据，可以尝试组合二个、三个不同的属性构造新的特征，如果存在时间相关属性，可以划出不同的时间窗口，得到同一属性在不同时间下的特征值，也可以把一个属性分解或切分，例如将数据中的日期字段按照季度和周期后者一天的上午、下午和晚上去构建特征。总之特征构建是个非常麻烦的问题，书里面也很少提到具体的方法，需要对问题有比较深入的理解。

三、特征提取

1. PCA主成分分析

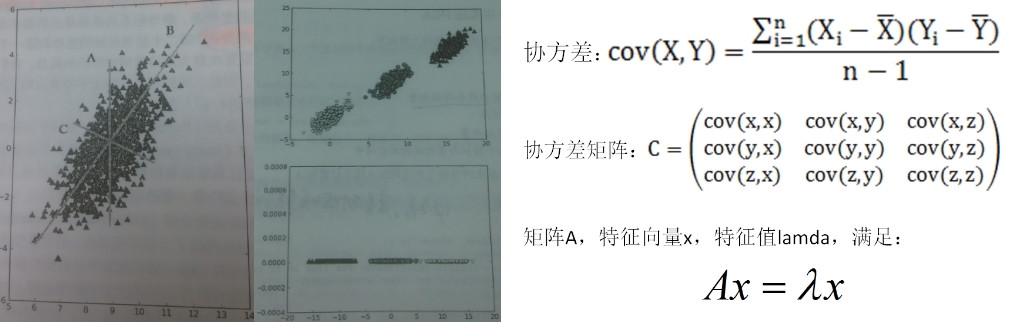
         PCA的思想是通过坐标轴转换，寻找数据分布的最优子空间，从而达到降维、去相关的目的。下面的图是直接从《机器学习实战》中截取的，原始数据二维特征，三分类问题，左图是原始数据。进行PCA特征转换，第一个新坐标轴选择的是原始数据中方差最大的方向（线B），第二个新坐标轴与第一个坐标轴正交且具有最大方差的方向（线C），当特征维度较多时，重复上述过程，会发现大部分的方差都包含在前几个新的坐标轴中，通过选择保留前N个坐标轴达到降维的效果，下面中上是特征转换的图右，中下是降维后的图。在数学上，是先用原始数据协方差矩阵的前N个最大特征值对应的特征向量构成映射矩阵，然后原始矩阵左乘映射矩阵，从而对原始数据降维。下图右面列出了两个随机变脸之间协方差的计算公式、怎么计算矩阵的协方差矩阵、矩阵的特征值、特征向量。特征向量可以理解为坐标准换中的新坐标轴的方向，特征值表示矩阵在对应的特征向量上的方差，特征值越大，方差越大，信息量越多。

2. LDA线性判别分析

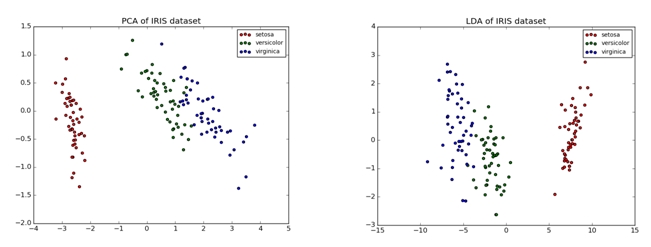
       LDA的原理是将带上标签的数据（点），通过投影的方法，投影到维度更低的空间，使得投影后的点，会形成按类别区分，相同类别的点，将会在投影后更接近，不同类别的点距离越远。skearn网站上面有个例子介绍PCA与LDA的区别，分别通过PCA和LDA将4维特征三分类的Iris数据降维为2维特征，然后再进行分类，效果差不多，可视化出来发现有些不同，毕竟降维方式有些不同。

 

LDA算法的主要步骤：

1：分别计算每个类别i的原始中心点

2.类别i投影后的中心点为：

3.衡量类别i投影后，类别点之间的分散程度，用方差来表示：

4.使用下面的式子表示LDA投影到w后的损失函数，最大化J(W)就可以求出最优的w，具体解法参考博客：

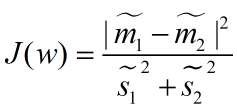
3. ICA独立成分分析

        PCA特征转换降维，提取的是不相关的部分，ICA独立成分分析，获得的是相互独立的属性。ICA算法本质寻找一个线性变换z = Wx，使得z的各个特征分量之间的独立性最大。ICA相比与PCA更能刻画变量的随机统计特性，且能抑制噪声。ICA算法听着有点绕，ICA认为观测到数据矩阵X是可以由未知的独立元举证S与未知的矩阵A相乘得到。ICA希望通过矩阵X求得一个分离矩阵W，使得W作用在X上所获得的矩阵Y能够逼近独立源矩阵S，最后通过独立元矩阵S表示矩阵X，所以说ICA独立成分分析提取出的特征中的独立部分。

四、特征选择

        特征选择是剔除不相关或者冗余的特征，减少有效特征的个数，减少模型训练的时间，提高模型的精确度。特征提取通过特征转换实现降维，特征选择则是依靠统计学方法或者于机器学习模型本身的特征选择（排序）功能实现降维。特征选择是个重复迭代的过程，有时可能自己认为特征选择做的很好，但实际中模型训练并不太好，所以每次特征选择都要使用模型去验证，最终目的是为了获得能训练出好的模型的数据，提升模型的性能。下面介绍几个常用的方法

1. 运用统计学的方法，衡量单个特征与响应变量（Lable）之间的关系。

• 皮尔森相关系数（Pearson Correlation），衡量变量之间的线性关系，结果取值为[-1,1]，-1表示完全负相关，+1表示正相关，0表示不线性相关，但是并不表示没有其它关系。Pearson系数有一个明显缺陷是，只衡量线性关系，如果关系是非线性的，即使连个变量具有一一对应的关系，Pearson关系也会接近0。皮尔森系数的公式为样本共变异数除以X的标准差和Y的标准差的乘积。sklearn中可以直接计算两个随机变量之间的Pearson相关系数，例如下面计算X与X*X之间的相关系数约为0。

x = np.random.uniform(-1, 1, 100000)

print pearsonr(x, x**2)[0]

-0.00230804707612

• 最大信息系数（MIC）。最大信息系数是根据互信息得到的，下面是互信息公式。最大信息系数MIC不仅能像Pearson系数一样度量变量之间的线性关系，还能度量变量之间的非线性关系。MIC虽然能度量变量之间的非线性关系，但当变量之间的关系接近线性相关的时候，Pearson相关系数仍然是不可替代的。第一、Pearson相关系数计算速度快，这在处理大规模数据的时候很重要。第二、Pearson相关系数的取值区间是[-1，1]，而MIC和距离相关系数都是[0，1]。这个特点使得Pearson相关系数能够表征更丰富的关系，符号表示关系的正负，绝对值能够表示强度。当然，Pearson相关性有效的前提是两个变量的变化关系是单调的。下面列举了MIC和Pearson系数在变脸处于不同关系下的表现情况。

 2. 基于机器学习模型的特征选择

        线性模型和正则化

　　当特征和响应变量之间全部都是线性关系，并且特征之间均是比较独立的。可以尝试使用线性回归模型去做特征选择，因为越是重要的特征在模型中对应的系数就会越大，而跟输出变量越是无关的特征对应的系数就会越接近与0。在很多实际的数据当中，往往存在多个互相关联的特征，这时候模型就会变得不稳定，数据中细微的变化就可能导致模型的巨大变化（模型的变化本质上是系数，或者叫参数，可以理解成W），这会让模型的预测变得困难，这种现象也称为多重共线性。例如，假设我们有个数据集，它的真实模型应该是Y=X1+X2，当我们观察的时候，发现Y’=X1+X2+e，e是噪音。如果X1和X2之间存在线性关系，例如X1约等于X2，这个时候由于噪音e的存在，我们学到的模型可能就不是Y=X1+X2了，有可能是Y=2X1，或者Y=-X1+3X2。通过在模型中加入正则化项，也能起到特征选择的作用。L1正则化学到的是比较稀疏的模型，控制惩罚项系数alpha，会迫使那些弱的特征所对应的系数变为0，这个特征使得L1正则化成为一种很好的特征选择方法。L2正则化会使得系数的取值变得平均，对于关联特征，这意味则他们能够获得更加相近的对应系数。

        随机森林模型

        随机森林由多棵决策树构成，决策树中的每个节点，都是关于某个特征的条件，利用不纯度可以确定划分数据集的最优特征，对于分类问题，通常采用基尼不纯度或者信息增益，对于回归问题，通常采用方差或者最小二乘拟合。当训练决策树的时候，可以计算出每个特征减少了多少树的不纯度。对于一个决策树森林来说，可以算出每个特征平均减少了多少不纯度，并把它平均减少的不纯度作为特征选择的值。

       另一种常用的特征选择方法就是直接度量每个特征对模型精确率的影响。主要思路是打乱每个特征的特征值顺序，并且度量顺序变动对模型的精确率的影响。很明显，对于不重要的变量来说，打乱顺序对模型的精确率影响不会太大，但是对于重要的变量来说，打乱顺序就会降低模型的精确率。

要记住：1、这种方法存在偏向，对具有更多类别的变量会更有利；2、对于存在关联的多个特征，其中任意一个都可以作为指示器（优秀的特征），并且一旦某个特征被选择之后，其他特征的重要度就会急剧下降，因为不纯度已经被选中的那个特征降下来了，其他的特征就很难再降低那么多不纯度了，这样一来，只有先被选中的那个特征重要度很高，其他的关联特征重要度往往较低。在理解数据时，这就会造成误解，导致错误的认为先被选中的特征是很重要的，而其余的特征是不重要的，但实际上这些特征对响应变量的作用确实非常接近的（这跟Lasso是很像的）。

     特征工程内容很多，关系特征选，强烈建议仔细看结合Scikit-learn介绍几种常用的特征选择方法，则篇干货的结尾有个例子比较了集中特征方法对每个特征的评分，非常值得学习，就我自己而言由于很少碰到线性问题，所以使用RF做特征选择的情况会多一些。

 

参考资料：

1. 特征工程技术和方法概括总结：http://blog.csdn.net/jasonding1354/article/details/47171115 

2. 干货：结合Scikit-learn介绍几种常用的特征选择方法：http://dataunion.org/14072.html 

3. 参考资料2的英文原版：http://machinelearningmastery.com/discover-feature-engineering-how-to-engineer-features-and-how-to-get-good-at-it/ 

4. 机器学习之特征工程：http://www.csuldw.com/2015/10/24/2015-10-24%20feature%20engineering/ 

5. 特征提取与特征选择： http://lanbing510.info/2014/10/22/Feature-Extraction-Selection.html 

6. PCA与LDA：http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html