计算成像资料笔记
【来源】:
超星视频 > 超星课堂 > 计算机系统结构 > 计算成像与超分辨率图像重建
有计算机参与的成像行为都可以认为是计算成像。
Computational Imaging(Photograph)
传统成像是所见即所得
借助计算机对图像重建、还原。计算成像能够实现传统成像无法完成的任务:如去除运动模糊、超分辨率成像。
研究比较多的:
- 照明方面的计算成像(Computational illumination),对快门编码(coded exposure)编码曝光。曝光时间、积分时间得到图像。
- 光学方面的计算成像(Computational optics),对孔径编码(coded aperture)aperture光圈、光阑,F数:镜头F1.2分辨率很高了,F2.8没法和1.2比。
- 信号处理方面的计算成像(Computational processing),non-optically coded images
- 探测器上的计算(Computational sensors),硬件上的探测器将探测与信号处理结合。
阿贝成像原理(Abbe):二次衍射成像理论。目标在像平面上成像,最开始会有一个频率分配的问题,目标上面每一点都会出现若干频率的信号,经过光学系统,再经过焦平面再对频率进行进一步的分配,最后在像平面上成像。
提出了显微镜分辨率存在上限,即光学衍射极限。很难突破200nm。可以利用随机介质成像来突破200nm。衍射受限系统,只有孔径之内的频率可以进来,超出孔径之外的频率进不来。频率,是看作光栅形式,光栅以波长为单位,可以计算出频率,大概算出光学系统的分辨率。
阿贝原理提出:显微镜的分辨率和光的波长、显微镜物镜孔径的关系式。
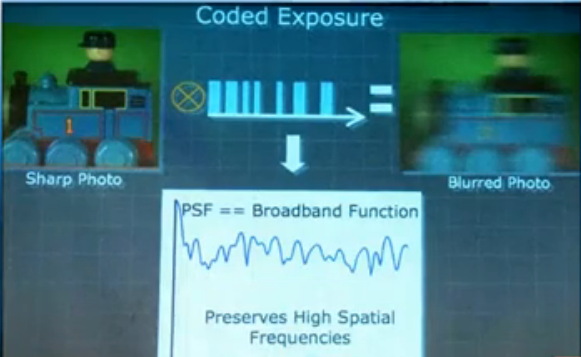
编码曝光:(coded exposure)
人眼可以容忍噪声,忍受不了模糊。运动模糊=原图*卷积上曝光时间PSF。
PSF中可以发现会有很多零值(0)或接近零的值。PSF本身是sinc函数。g=f*h,复原的时候,进行逆卷积的时候会有除0的情况,图像恢复的噪声很严重,得不到正确的信息,因此效果不好。这种方式去模糊,模型找的很好,但计算方法有问题。
对曝光进行编码,让PSF值不再为0。broadband function。
曝光就是光圈和快门的组合:一张正确曝光的图片可以有N种不同的光圈和快门速度组合,可以这样认为:光圈(值)大小其实就是那个小圆窗户开多大,快门(速度)就是窗户打开多久。假设窗户只打开1/4,时间为4秒钟可以正确曝光的话,很显然,窗户打开一半,时间2秒钟也能让底片正确曝光,因为1/4*4=1/2*2=1,进光量都是一样多。
光圈与F数相关知识 - ostartech - 博客园 https://www.cnblogs.com/wxl845235800/p/9436071.html
编码孔径(coded aperture):
五边形孔径:对模糊图像重建,选取不合适的尺寸(大不好、小还可以)合适尺寸好的。合适不合适与否是人主观来看的,计算机分辨不出来。
如果利用编码孔径,不合适的尺寸(大、小都不好)是错的,只有合适尺寸才是对的。
这时可以把图像模糊的程度精确的估计出来,用来做全景深图像的恢复。拍摄图像对其重聚焦。
利用不同孔径对图像深度来进行估计。优化,可以用不同颜色来体现目标在场景中的不同深度。
传统的编码孔径成像:
来源于小孔成像,多个孔的成像重叠。
编码模板可以是二值可以是多值(可以使用液晶调制方式来形成)。用二值的编码模板结果处理后噪声多,而多值编码模板噪声少。
选用合适大小的孔径重建。

目标经过编码模板成像,可以理解为是若干个小孔成像叠加。
压缩编码孔径成像:
利用压缩感知理论,(Compressive Sensing,Compressed Sampling,CS),在光学成像系统中加入随机编码孔径,作为预测矩阵,实现压缩感知采样。做了降采样,目的是来完成超分辨率重建。
采样是在低分辨率CCD上完成的,通过CS理论的图像超分辨率重建,可以获得4x及以上的高分辨率图像。
编码过程成像公式:加入了,D降采样。Y是得到图像的频谱,X是原图像拍摄所得目标,H是编码孔径,e是噪声。和一般的成像公式其实是一致的。只不过多加了降采样的操作,分为m个小块。
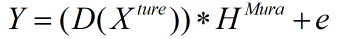
解码过程(逆卷积)公式:
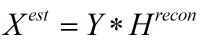
成像过程:目标经过编码孔径模板成像,会有很多像,这些像叠加在一起。即若干个小孔成像叠加在一起,再经过计算机解码,得到复原图像。
压缩感知理论:在一维成立,二维不一定成立。所以在对图像压缩编码孔径时,要把其从二维展到一维操作,这个过程应该讲是不严格的,因此压缩编码理论已经慢慢不是很热门了。但是压缩编码中的方法很多在扩展的应用:光谱成像中。
二值模板,多值模板。
分时压缩编码孔径成像:连续多次拍摄场景,更换不同模板(观测矩阵是不同的),结果会更好。CCD分辨率可以更低。可以重建出更高分辨率图像。
原图->1/4采样->压缩编码孔径成像进行超分辨率重建
随机散射SR成像:
随机散射介质可以扩展透过光学系统的空间带宽,在光学系统中加入随机介质,可以增大光学系统的数值孔径(NA)。
论文:2007年,Random Projections Imaging with Extended Space-band width Product。
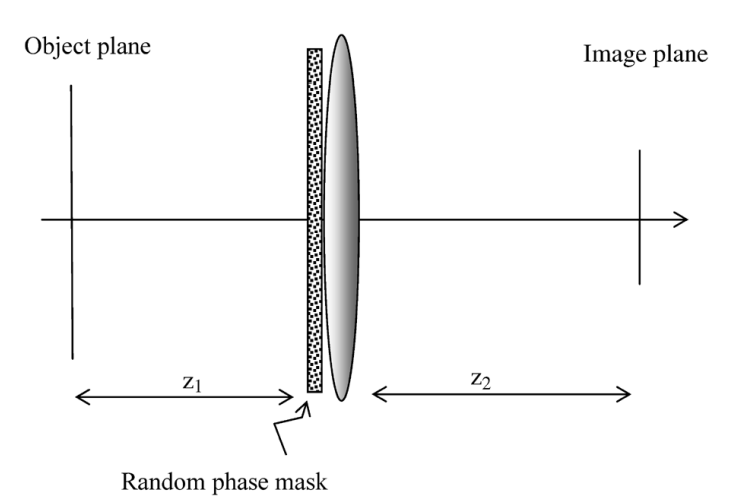
在透镜前面加上随机介质,毛玻璃。成像不清晰,但PSF可以变得更窄,带宽可以进入更多。
这种理论在90年代末,已经有人在声学方面做散射类似研究。
借助压缩感知理论进行重建。
量子成像:
鬼成像,利用光源及探测光场的非经典量子特性获取图像信息。
应用于空间遥感领域,可大大降低空间平台上成像系统的复杂性,特别适合于微小卫星遥感应用。
利用纠缠光子成像难题:纠缠光源的产生、纠缠光子的传输、纠缠光子的检测、量子图像的重建。
增大景深:
全景深:传统利用小光圈获得大景深,但曝光时间要很长,同时还有其他很多问题。
利用编码孔径方式精确估计出各个的模糊程度,用不同的孔径对深度进行估计。目标在场景中不同深度。
增大景深与全景深成像 - ostartech - 博客园 https://www.cnblogs.com/wxl845235800/p/9408684.html
光场相机:
见 ,光场相机 - ostartech - 博客园 https://www.cnblogs.com/wxl845235800/p/9042374.html
【其他文献】
写的很棒的一篇综述类博客:计算摄像学研究 https://blog.csdn.net/XWUkefr2tnh4/article/details/78955485
【笔记来自于】
在超星上的其他学术视频:光电成像、计算成像。