图像空域活动性测度
图像复原是一个病态(或非适定)问题的求逆过程，且在这个过程中为受噪声的影响，为了更好的处理这种情况，需要采用平滑约束法。
其思想为：设置dc使得dtcx为期望图像的平滑性测度，也可称为空域活动性测度，
测度越大(越不平滑)，复原图像的概率越小，这样使得复原结果的高频分量得到有效的抑制。
为了能够保留图像边缘信息，可以利用Huber所提出的一个新函数，称为Huber边缘惩罚函数：
ρ(dtcx,T)=(dtcx)2,|dtcx|≤TT2+2T(|dtcx|-T),|dtc|>T]]> 可以看出，这种函数保留了凸集特性。
关于T的取值方法，可以对对像素xi，j的二阶邻域系统所有像素灰度值取均值，即令：
MT=19Σk=i-1i+1Σl=j-1j+1xk,l]]>
则阈值T的取值规则可表示为：
式中，β为某一预先设定值如可设为噪声标准方差的估计。如果xi，j与MT之差的绝对值大于β，则有理由认为该像素点属于图像边缘，此时将T取较小值，由线性函数进行对该像素点计算；相反情况，则T取较大值，由Huber函数中二次函数对像素点处理。从而因T值不同而控制Huber函数边缘惩罚的区域，更好地保护图像的细节。分别将条件概率模型和先验概率模型带入，即可经过迭代求得MAP估计问题的最优解。这一求解，算法是可实现的。
文献浏览 http://www.pss-system.gov.cn/sipopublicsearch/patentsearch/showViewList-jumpToView.shtml
采用图像的多尺度小波表征来定义图像的空域活动性测度,并由此构建多尺度Huber-Markov先验模型。
有较好的图像边缘保持能力。
采用具有边缘保持能力的 Huber-Markov 模型作为超分辨率图像的先验模型。
其 Gibbs 概率密度函数为：
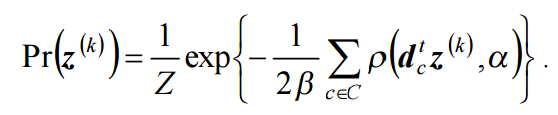
Z 是归一化常数,b是 Gibbs 先验的温度参数,c 是一个局部像素组,称为团块,而图像上所有的团块构成集合C。
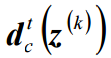空域活动性测度。在超分辨率图像的平滑区域值较小；而在边缘区域的值较大。
Huber边缘惩罚函数定义如下：
阈值参数a控制先验模型的不连续性大小。
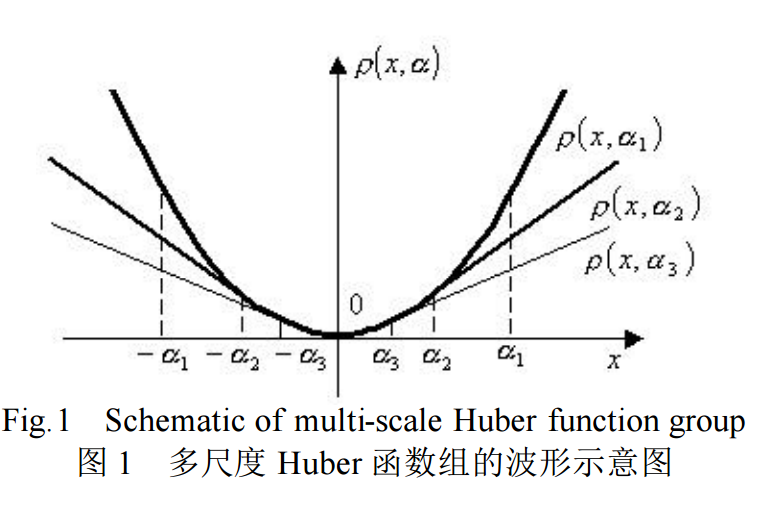
多尺度 Huber函数组对大尺度子带图像中的边缘惩罚性较弱，对小尺度子带图像中的边缘惩罚性较强。
Huber 函数是凸的,所以目标函数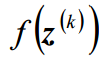
存在惟一最优解，可以用梯度下降最优化方法来获得超分辨率图 像的估计。
【文献】张新明 等:基于多尺度边缘保持正则化的超分辨率复原
一种以超分辨率理论为基础的磁共振眼球成像方法.pdf https://max.book118.com/html/2018/0314/157314515.shtm
不适定的求解问题。为解决反演的多解性、提高反演稳定性,通常在反演过程中加入一个正则化约束。Tikhonov方法得到的是平滑解,能有效压制噪声,但会使边缘模糊;全变分方法能很好地保护边缘,但压制噪声效果欠佳。为了在压制噪声的同时有效保护边缘信息,采用马尔科夫随机场约束,Huber函数作为势函数,通过合理设置阈值,实现Huber惩罚函数的约束效果。
