[Agc011F] Train Service Planning
[Agc011F] Train Service Planning
题目大意:
有n+1个车站,n条轨道,第i条轨道联通i-1和i车站,通过它要花a[i]时间,这条轨道有b[i]=1或2条车道,也就是说,他是单向还是双向的。
要满足以下约定
- 所有的火车要么从站台0到站台n,要么从站台n到站台0
- 对任意终点为n的火车,如果它在t时刻离开站台i−1并开往站台i,那么它必须在t+Ai时刻到达i站台,对反方向要求相同
- 对任意终点为n的火车,如果它在s时刻到达站台i并在t时刻离开站台i,那么下一列经过站台i的终点为n的火车必须在s+K时刻到达站台i并在t+K时刻离开站台i,对反方向要求相同![]
- 在任意时刻不能有两列相向而行的火车在单向区间内互相穿过
要求最小化两种火车从起点到终点的时间和。
\(n\leq 10^5,a_i\leq 10^9\)
试题分析
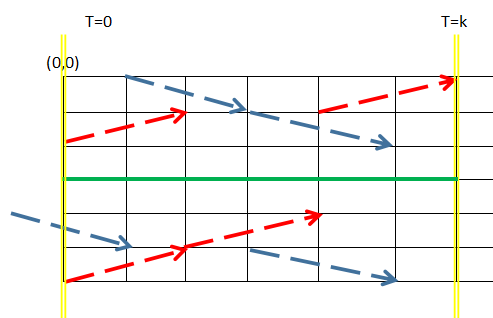
不难发现,双向道路上如果有两条线(列车行驶)的交是没有问题的,因为可以双向行驶。
但是单向的话就不行了,需要在某个车站进行等待并交换道路。
然而我们需要求这些车的行驶时间的和,怎么办呢?
一个非常重要的传统办法——列式子。
我们下面把第一辆车称作1号,把第二辆(\(n\to 0\))称作2号。
设\(q_i\)为1号每站的等待时间,\(p_i\)为2号每站的等待时间。
于是有:\(tim_1=\sum_{i=0}^{n-1} q_i+a_i,tim_2=\sum_{i=0}^{n-1} p_i+a_i\)
那么走到其中一个点\(j\)的时间是多少呢?
还是没有突破口,继续列式子。。。
发现1号走过\(j-1\to j\)的时间区间是\((\sum_{i=0}^{j-2} q_i+a_i +q_{j-1},\sum_{i=0}^{j-1} q_i+a_i)\)
2号同理。
这个东西乍一看没有办法搞,但是这道题有一个很重要的性质:时间K就是一个循环节。
那么我们就可以把这个东西丢到\(\pmod{k}\)的意义下去做。
既然图上的线不交,就意味着1号和2号的站中间的时间区间不交。
于是继续列出限制条件,然后移项变换,得到:$$\sum_{i=0}^{j}(p[i]+q[i])\not \in[-2s[j],-2(s[j]-a[j])]$$
其中\(s\)为\(a\)的前缀和。
那么问题就变成了:
有一个人,在数轴上走,从左到右每次向右走(可以不走),每次走的地方在\([l_i,r_i]\)中,问代价。
因为是\(\pmod{k}\)意义下,所以可以把两段补区间前后相接得到一个新的区间。
能在原地踏步显然在原地踏步,所以我们需要找的是\([l_j,r_j]\)不包含\(l_i\)的\(j>i\)的区间。
这个东西我们可以线段树的区间覆盖加上贪心dp出来。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<algorithm>
//#include<ctime>
//#include<cmath>
//#include<queue>
using namespace std;
#define LL long long
inline int read(){
int x=0,f=1; char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*f;
}
const LL INF = 2147483600;
const LL MAXN = 300010;
LL N,K;
LL tag[MAXN<<2],col[MAXN<<2];
inline void tage_lazy(LL rt){
if(tag[rt]){
col[rt<<1]=tag[rt]; col[rt<<1|1]=tag[rt];
tag[rt<<1]=tag[rt]; tag[rt<<1|1]=tag[rt];
tag[rt]=0;
}
}
inline void Cover(LL rt,LL l,LL r,LL L,LL R,LL k){
if(L>R) return ;
if(L<=l&&R>=r){tag[rt]=k; col[rt]=k; return ;} tage_lazy(rt);
LL mid=(l+r)>>1; if(L<=mid) Cover(rt<<1,l,mid,L,R,k);
if(R>mid) Cover(rt<<1|1,mid+1,r,L,R,k); return ;
}
inline LL Query(LL rt,LL l,LL r,LL k){
if(l==r) return col[rt]; LL mid=(l+r)>>1; tage_lazy(rt);
if(k<=mid) return Query(rt<<1,l,mid,k);
else return Query(rt<<1|1,mid+1,r,k);
}
LL f[MAXN+1],Num[MAXN<<1];
LL l[MAXN+1],r[MAXN+1],tot;
inline LL Ask(LL k){
LL pos=Query(1,1,tot,k);
return (pos?f[pos]+(Num[l[pos]]-Num[k]+K)%K:0);
}
LL a[MAXN+1],b[MAXN+1],s[MAXN+1];
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
N=read(),K=read(); tot=0;
for(LL i=1;i<=N;i++){
a[i]=read(),b[i]=read();
s[i]=(s[i-1]+a[i]);
if(b[i]==2){l[i]=0; r[i]=K-1;}
else l[i]=(K-2*s[i-1]%K)%K,r[i]=(K-2*s[i]%K)%K;
if(b[i]==1&&a[i]*2LL>K){puts("-1"); return 0;}
Num[++tot]=l[i]; Num[++tot]=r[i];
//cout<<"x:"<<l[i]<<" "<<r[i]<<endl;
} sort(Num+1,Num+tot+1); tot=unique(Num+1,Num+tot+1)-Num-1;
for(LL i=1;i<=N;i++){
l[i]=lower_bound(Num+1,Num+tot+1,l[i])-Num;
r[i]=lower_bound(Num+1,Num+tot+1,r[i])-Num;
} for(LL i=N;i>=1;i--){
f[i]=Ask(l[i]);
if(l[i]>r[i]) Cover(1,1,tot,r[i]+1,l[i]-1,i);
else Cover(1,1,tot,1,l[i]-1,i),Cover(1,1,tot,r[i]+1,tot,i);
} LL ans=f[1];
for(LL i=tot;i>=1;i--) ans=min(ans,Ask(i));//cout<<i<<": "<<Ask(i)<<endl;
printf("%lld\n",ans+2LL*s[N]);
return 0;
}


