[BZOJ4422] [Cerc2015]Cow Confinement
[BZOJ4422] [Cerc2015]Cow Confinement
Description
一个106行106列的网格图,上面有一些牛、花和一些矩形围栏,围栏在格子的边界上,牛和花在格子里,牛只能向下或向右走,牛也不能穿过围栏和地图边界,求每头牛它能到达的花的数量。注意栅栏不会相交
Input
第一行一个数f表示矩形围栏的数量。接下来f行,每行四个数x1,y1,x2,y2,表示(x1,y1)在围栏内部矩形的左上角,(x2,y2)在右下角。接下来一行一个数m表示花的数量。接下来m行每行两个数x,y,表示在(x,y)处有一朵花。接下来一行一个数n表示牛的数量。接下来n行每行两个数x,y,表示在(x,y)处有一头牛。
Output
总共n行,每行一个数ans,第i个数表示第i头牛能到ans个花。
Sample Input
4
2 2 8 4
1 9 4 10
6 7 9 9
3 3 7 3
9
3 4
8 4
11 5
10 7
10 8
9 8
2 8
4 11
9 11
8
1 1
5 10
6 9
3 7
7 1
4 2
7 5
3 3
Sample Output
5
1
0
1
3
1
3
0
HINT
0<=f<=200000
0<=m<=200000
1<=n<=200000
试题分析
神题毒瘤题二合一系列
毕竟是Cerc2015的防AK题
我们首先可以列出一个很暴力的转移方程:\(f_{i,j}\)表示从\((i,j)\)出发可以到达多少个花。
然后讨论许许多多的情况并转移。复杂度:\(O((n+m+f)^2)\)。
这种东西二维数点+容斥做不了,可以被特殊数据卡成时空复杂度均\(O(qn)\)。
那么就是数据结构优化\(dp\)喽,但单看转移方程并没有办法优化。
通常在这种情况下我们有两类手段:
- 差分
- 前缀和优化
这怎么看也不想前缀和优化啊,差分显然更靠谱。
由于是右下角,所以注意扫描线从右到左扫描。
怎么差分呢?我们不妨设\(g{i,j}=f_{i,j}-f_{i+1,j}\),也就是当前行i比它下面一个格子(i+1,j)可以多多少花。
那么更形象一点来说就是(i,j)可以走到多少从(i+1,j)走不到的花。
这样的话遇见一朵花就单点+1即可。
如果我们遇到了一个新的区间怎么办呢?
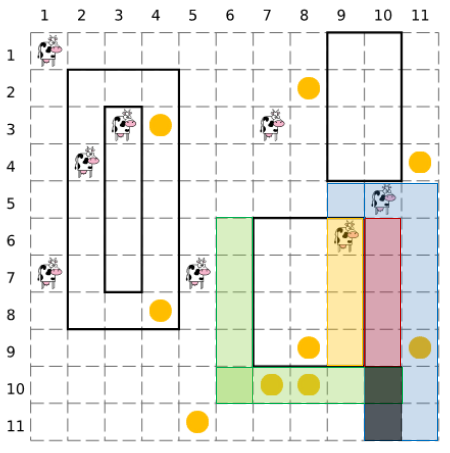
可以发现,最左上角的蓝色格子以及上面(假设还有格子)的若干格子都还可以走到红色部分,而新增矩形下方的从来就不可以走到。
所以\((x_l-1,y)\)要加上红色部分+黑色部分(从黑格子到下一个框)的区间和,++因为当询问矩形上面的点时,我们需要走到右下去++,并且把黄色区间置零。
注意我们是从上往下扫的,所以如果黄色区间中有花就还可以加上。
删除一个区间怎么办呢?
首先还是区间置0(竖着的浅绿色区间),因为两两之间都一样了。
还要考虑左上角的格子(5,6),这个格子照样有向右走的“特权”,所以在这一点上不用变动。
但是这里有一个需要注意的地方:注意黑色格子,这个格子到最下面(下一个框)会被当前点向右走再向下走计算一遍,并且会被向下走再向右走计算一遍,所以要减一遍,我们可以在区间加入的时候把这个答案先询问好。
查询的话显然就是从奶牛到它下面的第一个栅栏的区间和。
一定要注意在线段树中加入不合法特判。
咕咕咕代码在线修补完成
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<algorithm>
//#include<ctime>
//#include<cmath>
//#include<queue>
#include<set>
using namespace std;
#define LL long long
#define rr register
namespace IO
{
const int S=(1<<20)+5;
//Input Correlation
char buf[S],*H,*T;
inline char Get()
{
if(H==T) T=(H=buf)+fread(buf,1,S,stdin);
if(H==T) return -1;return *H++;
}
inline int read()
{
rr int x=0;rr char c=Get();
while(!isdigit(c)) c=Get();
while(isdigit(c)) x=x*10+c-'0',c=Get();
return x;
}
inline void reads(char *s)
{
rr char c=Get();rr int tot=0;
while(c<'a'||c>'z') c=Get();
while(c>='a'&&c<='z') s[++tot]=c,c=Get();
s[++tot]='\0';
}
//Output Correlation
char obuf[S],*oS=obuf,*oT=oS+S-1,c,qu[55];int qr;
inline void flush(){fwrite(obuf,1,oS-obuf,stdout);oS=obuf;}
inline void putc(char x){*oS++ =x;if(oS==oT) flush();}
template <class I>inline void print(I x)
{
if(!x) putc('0');
if(x<0) putc('-'),x=-x;
while(x) qu[++qr]=x%10+'0',x/=10;
while(qr) putc(qu[qr--]);
}
}
using namespace IO;
const int INF = 2147483600;
const int MAXN = 200010;
const int Y = 1000000;
struct data{
int y,l,r,opr,x,id;
}q[MAXN<<3];
int N,M,C;
bool cmp(data a,data b){
if(a.y!=b.y) return a.y>b.y;
if(a.opr==1) return 0;
if(b.opr==1) return 1;
if(a.x!=b.x) return a.x<b.x;
return a.opr>b.opr;
}
multiset<int> s;
multiset<int>::iterator it,it2;
int ret[MAXN<<1];
bool rev[Y*4+10]; int sum[Y*4+10];
int tot=0;
inline int Down(int x){
it=s.upper_bound(x); return (*it)-1;
}
inline void tage_lazy(int rt){
if(rev[rt]) {
sum[rt<<1]=sum[rt<<1|1]=0;
rev[rt]=0; rev[rt<<1]=rev[rt<<1|1]=1;
} return ;
}
inline void Init(int rt,int l,int r,int L,int R){
if(L>R||!L||R>Y) return ;
if(L<=l&&R>=r){rev[rt]=1; sum[rt]=0; return ;}
int mid=(l+r)>>1; tage_lazy(rt);
if(L<=mid) Init(rt<<1,l,mid,L,R);
if(R>mid) Init(rt<<1|1,mid+1,r,L,R);
sum[rt]=sum[rt<<1]+sum[rt<<1|1]; return ;
}
inline void Add(int rt,int l,int r,int k,int x){
if(!k||k>Y) return ;
if(l==r){sum[rt]+=x; return ;} tage_lazy(rt);
int mid=(l+r)>>1; if(k<=mid) Add(rt<<1,l,mid,k,x);
else Add(rt<<1|1,mid+1,r,k,x); sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
inline int Query(int rt,int l,int r,int L,int R){
if(L>R||!L||R>Y) return 0;
if(L<=l&&R>=r) return sum[rt]; tage_lazy(rt);
int mid=(l+r)>>1,ans=0; if(L<=mid) ans+=Query(rt<<1,l,mid,L,R);
if(R>mid) ans+=Query(rt<<1|1,mid+1,r,L,R);
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
return ans;
}
int ans[MAXN+1];
int main(){
N=read();
for(int i=1;i<=N;i++){
int x1=read(),y1=read(),x2=read(),y2=read();
q[++tot].y=y2; q[tot].x=x1; q[tot].l=x1; q[tot].r=x2; q[tot].opr=3; q[tot].id=i;
q[++tot].y=y1-1; q[tot].x=x1; q[tot].l=x1; q[tot].r=x2; q[tot].opr=4; q[tot].id=i;
}
M=read();
for(int i=1;i<=M;i++){
q[++tot].x=read(); q[tot].y=read(); q[tot].opr=2;
}
C=read();
for(int i=1;i<=C;i++){
q[++tot].x=read(); q[tot].y=read(); q[tot].opr=1;
q[tot].id=i;
} sort(q+1,q+tot+1,cmp);
int j=1; s.insert(0); s.insert(Y+1);
for(int i=Y;i>=1;i--){
while(j<=tot&&q[j].y==i){
if(q[j].opr==4){
Init(1,1,Y,q[j].l,q[j].r);
Add(1,1,Y,q[j].l-1,-ret[q[j].id]);
s.erase(s.find(q[j].l)); s.erase(s.find(q[j].r+1));
} else if(q[j].opr==3){
int pos=Down(q[j].r+1),su=0;
ret[q[j].id]=Query(1,1,Y,q[j].r+1,pos);
su=Query(1,1,Y,q[j].l,q[j].r);
Add(1,1,Y,q[j].l-1,su+ret[q[j].id]);
Init(1,1,Y,q[j].l,q[j].r);
s.insert(q[j].l); s.insert(q[j].r+1);
} else if(q[j].opr==2){
Add(1,1,Y,q[j].x,1);
} else{
int pos=Down(q[j].x); it=s.upper_bound(q[j].x);
ans[q[j].id]=Query(1,1,Y,q[j].x,pos);
}
++j;
}
} for(int i=1;i<=C;i++){
printf("%d\n",ans[i]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号