kruskal算法
kruskal算法
【算法定义】
假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网,则按Kruskal算法构造最小生成树的过程为:先构造一个只含 n 个顶
点,而边集为空的子图,若将该子图中各个顶点看成是各棵树上的根结点,则它是一个含有 n 棵树的一个森林。之后,从网的
边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,也就是说,将这两个顶点分别所在的
两棵树合成一棵树;反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类
推,直至森林中只有一棵树,也即子图中含有 n-1条边为止,可见题:
【海岛帝国系列赛】No.4 海岛帝国:LYF的太空运输站
上面有转自百科的分析,是一道最小生成树算法的题。一个有N条边的连通图,如果让它不连通,那么它要有N-1条边。
算法过程:
1.将图各边按照权值进行排序
2.将图遍历一次,找出权值最小的边,排序就可以实现,查找可以用并查集实现,(条件:此次找出的边不能和已加入最小生成树集合的边构成环),若符合条件,则加入最小生成树的集合中。不符合条件则继续遍历图,寻找下一个最小权值的边。
那么,排序有没有快的树上搜索呢?
当然有,我们可以每当插入一个节点,和它的左儿子右儿子比较,如果大,就把此节点向下一层移动,而对应的后代向上移动,然后遍历整个树。
来看看这一道题吧:神奇的排序
总体来说就是排序,虽然时间限制宽的桶排序也能过QAQ
但我们今天讲的是树,
来看看具体的代码吧,用了个堆排序:
#include<iostream>
using namespace std;
int h[81];
int n;
void swap(int x,int y)//交换节点权值
{
int t;
t=h[x];
h[x]=h[y];
h[y]=t;
return ;
}
void siftdown(int i)//编号i的节点向下移动
{
int t,flag=0;
while(i*2<=n&&flag==0)
{
if(h[i]<h[i*2]) t=i*2;
else t=i;
if(i*2+1<=n)
if(h[t]<h[i*2+1])
t=i*2+1;
if(t!=i)
{
swap(t,i);
i=t;
}
else flag=1;
}
return ;
}
void creat()//建堆
{
int i;
for(i=n/2;i>=1;i--) siftdown(i);
return ;
}
void heapsort()//对堆排序
{
while(n>1)
{
swap(1,n);
n--;
siftdown(1);
}
return ;
}
int main()
{
int i,num;
scanf("%d",&num);
for(i=1;i<=num;i++) scanf("%d",&h[i]);
n=num;
creat();//一定要先建造堆
heapsort();
printf("%d",h[1]);
for(i=2;i<=num;i++) printf(" %d",h[i]);
}
下面,我们来看一看LYF的太空站那一题的树上排序。
树上排序如果数据小时间跟桶排序等排序差不多,甚至可能比归并和快排慢一些,但是却很实用,树上排序用它还是不错的。
【实例代码】
#include<iostream>
using namespace std;
int dis[20],book[20]={0};
int h[20],pos[20],size;
void swap(int x,int y)
{
int t;
t=h[x];
h[x]=h[y];
h[y]=t;
t=pos[h[x]];
pos[h[x]]=pos[h[y]];
pos[h[y]]=t;
return ;
}
void siftdown(int i)//节点向下转换
{
int t,flag=0;
while(i*2<=size&&flag==0)
{
if(dis[h[i]]>dis[h[i*2]]) t=i*2;
else t=i;
if(i*2+1<=size)
if(dis[h[t]]>dis[h[i*2+1]]) t=i*2+1;
if(t!=i)
{
swap(t,i);
i=t;
}
else flag=1;
}
return ;
}
void siftup(int i)//节点向上转换
{
int flag=0;
if(i==1) return ;
while(i!=1&&flag==0)
{
if(dis[h[i]]<dis[h[i/2]]) swap(i,i/2);
else flag=1;
i/=2;
}
return ;
}
int pop()//弹出
{
int t;
t=h[1];
pos[t]=0;
h[1]=h[size];
pos[h[1]]=1;
size--;
siftdown(1);
return t;
}
3.递归重复步骤1,直到找出n-1条边为止(设图有n个结点,则最小生成树的边数应为n-1条),算法结束。得到的就是此图的最小生成树。
转载的Kruskal算法代码:
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#define N 150
using namespace std;
int m,n,u[N],v[N],w[N],p[N],r[N];
int cmp(const int i,const int j) {return w[i]<w[j];}
int find(int x) {return p[x]==x?x:p[x]=find(p[x]);}
int kruskal()
{
int cou=0,x,y,i,ans=0;
for(i=0;i<n;i++) p[i]=i;
for(i=0;i<m;i++) r[i]=i;
sort(r,r+m,cmp);
for(i=0;i<m;i++)
{
int e=r[i];x=find(u[e]);y=find(v[e]);
if(x!=y) {ans += w[e];p[x]=y;cou++;}
}
if(cou<n-1) ans=0;
return ans;
}
int main()
{
int i,ans;
while(scanf("%d%d",&m,&n)!=EOF&&m)
{
for(i=0;i<m;i++)
{
scanf("%d%d%d",&u[i],&v[i],&w[i]);
}
ans=kruskal();
if(ans) printf("%d\n",ans);
else printf("?\n",ans);
}
return 0;
}
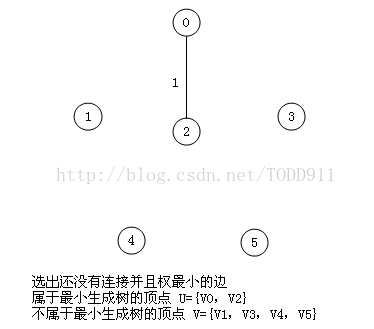
算法图解: