一文搞懂B树、B-树、B+树
前言
B树和B-树是同一种数据结构，如果不清楚的话，会被面试官忽悠，所以本文介绍两种数据结构，B树和B+树，废话不多数咱们开干。
B树
介绍
在计算机科学中，B树是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数量级的时间复杂度内完成。B树，其实是一颗特殊的二叉查找树（binary search tree），可以拥有多于2个子节点。与自平衡二叉查找树不同，B树为系统大块数据的读写操作做了优化。B树减少定位记录时所经历的中间过程，从而加快存取速度，其实B树主要解决的就是数据IO的问题。B树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库和文件系统的实现上。
特性
一个m阶的B树特点如下：
- 所有叶子节点都在同一层级；
- 除了根节点以外的其他节点包含的key值数量在[m/2]-1到m-1的数据范围；
- 除了根节点和叶子节点外，所有中间节点至少有m/2个孩子节点；
- 根节点如果不是叶子节点的话，它必须包含至少2个孩子节点；
- 拥有n-1个key值非叶子节点必须有n个孩子节点；
- 一个节点的所有key值必须是升序排序的；
以上六点就是B树的全部特性
检索
在B树种，检索操作类类似于二叉查找树。在二叉查找树中，检索开始于树的根节点，因为是二叉树所以每次有两种选择。在B树种检索中，也是开始于根节点，但每次需要比较n次（n是当前节点的所有子节点的数量）。在B树中，检索操作执行的时间复杂度是O(log n)，检索操作执行如下：
- 从输入获取读取检索元素；
- 和根节点的第一个元素进行比较；
- 如果匹配上，返回元素找到并且终止函数；
- 如果未匹配上，检查元数据与key值的大小；
- 如果小于待查元素，继续检索B树的左子树；
- 如果大于的话，比较相同节点中下一个key值并且重复3、4、5、6步，直到找到指定元素或者在树的叶子节点的最后一个结束；
插入
在B树种的插入操作，新元素一定是新添加在叶子节点的，具体操作流程如下：
- 检查树是否为空；
- 如果树为空，用新的插入元素创建一个新的节点并插入到树中并作为树的根节点；
- 如果树不为空，使用二叉查找树的逻辑为新元素找到一个叶子节点；
- 如果叶子节点中key有空位置，直接按照叶子节点内key值升序的原则将节点插入；
- 如果叶子节点中key已经满了，通过发送中间值到父节点，然后分裂叶子节点；重复这个操作，直到发送的中间值存储在一个节点中；
- 如果分裂发生在根节点，中间值将会成为树的新的根节点，树的高度将会加 1；
具体操作的演示示例如下所示：
删除
- 如果当前需要删除的key位于非叶子节点上，则用后继key（后继key，即右边叶子节点最左侧即为后继节点）覆盖要删除的key，然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子节点上，这个过程和二叉搜索树删除节点的方式类似。删除这个记录后执行第2步；
- 该节点key个数大于等于Math.ceil(m/2)-1（向下取整），结束删除操作，否则执行第3步；
- 如果兄弟节点key个数大于Math.ceil(m/2)-1，则父节点中的key下移到该节点，兄弟节点中的一个key上移，删除操作结束，即从兄弟节点中借一个元素过来；否则，将父节点中的key下移与当前节点及它的兄弟节点中的key合并，形成一个新的节点。原父节点中的key的两个孩子指针就变成了一个孩子指针，指向这个新节点。然后当前节点的指针指向父节点，重复上第2步。
有些节点它可能即有左兄弟，又有右兄弟，那么我们任意选择一个兄弟节点进行操作即可。
下面以5阶B树为例，介绍B树的删除操作，5阶B树中，节点最多有4个key,最少有2个key
a）原始状态
b）在上面的B树中删除21，删除后节点中的关键字个数仍然大于等2，所以删除结束。
c）在上述情况下接着删除27。从上图可知27位于非叶子节点中，所以用27的后继替换它。从图中可以看出，27的后继为28，我们用28替换27，然后在28（原27）的右孩子节点中删除28。删除后的结果如下图所示。
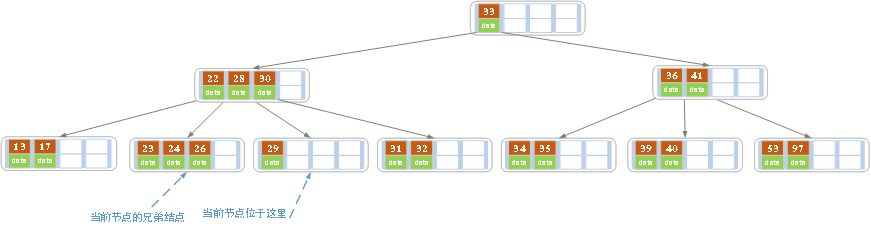
删除后发现，当前叶子节点的记录的个数小于2，而它的兄弟节点中有3个记录（当前节点还有一个右兄弟，选择右兄弟就会出现合并节点的情况，不论选哪一个都行，只是最后B树的形态会不一样而已），我们可以从兄弟节点中借取一个key。所以父节点中的28下移，兄弟节点中的26上移,删除结束。结果如下图所示。
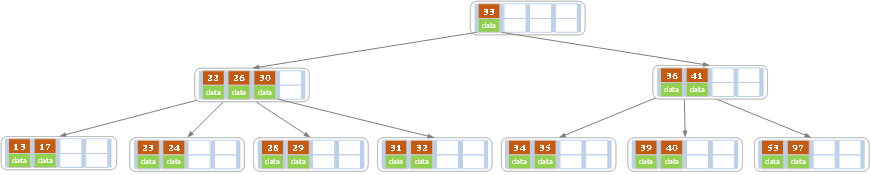
d）在上述情况下接着32，结果如下图。
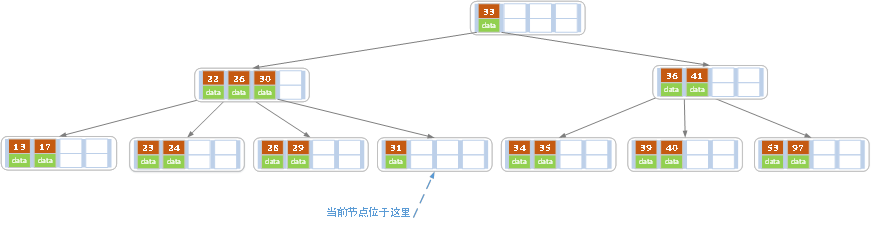
当删除后，当前节点中只key，而兄弟节点中也仅有2个key。所以只能让父节点中的30下移和这个两个孩子节点中的key合并，成为一个新的节点，当前节点的指针指向父节点。结果如下图所示。
当前节点key的个数满足条件，故删除结束。
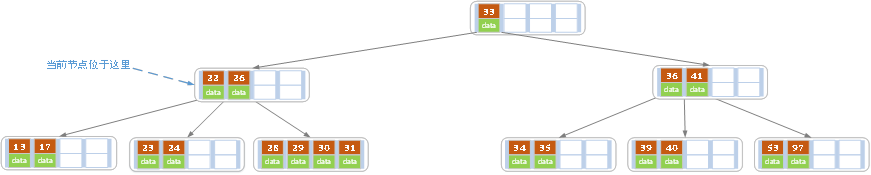
e）上述情况下，我们接着删除key为40的记录，删除后结果如下图所示。
同理，当前节点的记录数小于2，兄弟节点中没有多余key，所以父节点中的key下移，和兄弟（这里我们选择左兄弟，选择右兄弟也可以）节点合并，合并后的指向当前节点的指针就指向了父节点。
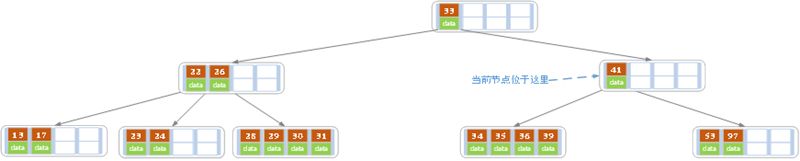
同理，对于当前节点而言只能继续合并了，最后结果如下所示。
合并后节点当前节点满足条件，删除结束。
小结
以上就是B树的特征以及操作过程，应该是说明白了，在生产环境中直接应用B树的场景比较少，但是B树是B+树的基础，所有很有必要把B树搞明白。
B+树
B+树是B树的变种，但不同资料中B+树的定义各有不同，其差异在于节点中关键字个数和孩子节点个数。一种是节点中关键字个数和孩子个数相同，另一种是关键字个数比孩子节点个数小1，这种方式是和B树基本相同。
特性
- B+树包含2种类型的节点：内部节点（也称索引节点）和叶子节点。根节点本身即可以是内部节点，也可以是叶子节点。根节点的关键字key个数最少可以只有1个；
- B+树与B树最大的不同是内部节点不保存数据，只用于索引，所有数据（或者说记录）都保存在叶子节点中；
- m阶B+树表示了内部节点最多有m-1个关键字（或者说内部节点最多有m个子树，和B树相同），阶数m同时限制了叶子节点最多存储m-1个记录；
- 内部节点中的key都按照从小到大的顺序排列，对于内部节点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子节点中的记录也按照key的大小排列；
- 每个叶子节点都存有相邻叶子节点的指针，叶子节点本身依关键字的大小自小而大顺序链接；
插入
- 若为空树，创建一个叶子节点，然后将记录插入其中，此时这个叶子节点也是根节点，插入操作结束。
- 针对叶子类型节点：根据key值找到叶子节点，向这个叶子节点插入记录。插入后，若当前节点key的个数小于等于m-1，则插入结束。否则将这个叶子节点分裂成左右两个叶子节点，左叶子节点包含前m/2个记录，右节点包含剩下的记录，将第m/2+1个记录的key进位到父节点中（父节点一定是索引类型节点），进位到父节点的key左孩子指针向左节点, 右孩子指针向右节点。将当前节点的指针指向父节点，然后执行第3步。
- 针对索引类型节点：若当前节点key的个数小于等于m-1，则插入结束。否则，将这个索引类型节点分裂成两个索引节点，左索引节点包含前(m-1)/2个key，右节点包含m-(m-1)/2个key，将第m/2个key进位到父节点中，进位到父节点的key左孩子指向左节点, 进位到父节点的key右孩子指向右节点。将当前节点的指针指向父节点，然后重复第3步，直到插入结束。
插入过程相对简单，这里不再举例。
删除
B+树的删除算法和B树的删除算法基本类似。叶子节点中如果没有相应的key值，删除失败。否则执行下面的步骤：
- 删除叶子节点中对应的key。删除后若节点的key的个数大于等于Math.ceil(m-1)/2 – 1，删除操作结束,否则执行第2步。
- 若兄弟节点key有富余（大于Math.ceil(m-1)/2 – 1），向兄弟节点借一个记录，同时用借到的key替换父结（指当前节点和兄弟节点共同的父节点）点中的key，删除结束。否则执行第3步。
- 若兄弟节点中没有富余的key,则当前节点和兄弟节点合并成一个新的叶子节点，并删除父节点中的key（父节点中的这个key两边的孩子指针就变成了一个指针，正好指向这个新的叶子节点），将当前节点指向父节点（必为索引节点），执行第4步（第4步以后的操作和B树就完全一样了，主要是为了更新索引节点）。
- 若索引节点的key的个数大于等于Math.ceil(m-1)/2 – 1，则删除操作结束。否则执行第5步
- 若兄弟节点有富余，父节点key下移，兄弟节点key上移，删除结束。否则执行第6步
- 当前节点和兄弟节点及父节点下移key合并成一个新的节点。将当前节点指向父节点，重复第4步。
注意，通过B+树的删除操作后，索引节点中存在的key，不一定在叶子节点中存在对应的记录。
下面通过一棵5阶B+树来说明上述算法的删除过程，5阶B+数的节点最少2个key，最多4个key。
a）初始状态
b）删除22,删除后结果如下图
删除后叶子结点中key的个数大于等于2，删除结束
c）删除15，删除后的结果如下图所示
删除后当前结点只有一个key,不满足条件，而兄弟结点有三个key，可以从兄弟结点借一个关键字为9的记录,同时更新将父结点中的关键字由10也变为9，删除结束。
d）删除7，删除后的结果如下图所示
当前结点关键字个数小于2，（左）兄弟结点中的也没有富余的关键字（当前结点还有个右兄弟，不过选择任意一个进行分析就可以了，这里我们选择了左边的），所以当前结点和兄弟结点合并，并删除父结点中的key，当前结点指向父结点。
此时当前结点的关键字个数小于2，兄弟结点的关键字也没有富余，所以父结点中的关键字下移，和两个孩子结点合并，结果如下图所示。
小结
以上是B+树的增删操作以及特性，在生产环境中常用做创建索引，与磁盘进行io。
对比
相比于二叉排序树，B树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程，从而加快存取速度，普遍运用在数据库和文件系统。
B和B+树的区别在于，B+树的非叶子结点只包含导航信息，不包含实际的值，所有的叶子结点和相连的节点使用链表相连，便于区间查找和遍历。B+ 树的优点在于：
由于B+树在内部节点上不包含数据信息，因此在内存页中能够存放更多的key。 数据存放的更加紧密，具有更好的空间局部性。因此访问叶子几点上关联的数据也具有更好的缓存命中率。
B+树的叶子结点都是相链的，因此对整棵树的便利只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻，所以缓存命中性没有B+树好。
但是B树也有优点，其优点在于，由于B树的每一个节点都包含key和value，因此经常访问的元素可能离根节点更近，因此访问也更迅速。
对于一颗节点为N度为M的子树，查找和插入需要log(M-1) N ~ log(M/2) N次比较。这个很好证明，对于度为M的B树，每一个节点的子节点个数为M/2 到 M-1之间，所以树的高度在log(M-1) N至log(M/2) N之间。
这种效率是很高的，对于N=62*1000000000个节点，如果度为1024，则logM/2N <=4，即在620亿个元素中，如果这棵树的度为1024，则只需要小于4次即可定位到该节点，然后再采用二分查找即可找到要找的值。
应用场景
B树和B+广泛应用于文件存储系统以及数据库系统中，在讲解应用之前，我们看一下常见的存储结构：
我们计算机的主存基本都是随机访问存储器(Random-Access Memory，RAM)，他分为两类：静态随机访问存储器（SRAM）和动态随机访问存储器（DRAM）。SRAM比DRAM快，但是也贵的多，一般作为CPU的高速缓存，DRAM通常作为内存。这类存储器他们的结构和存储原理比较复杂，基本是使用电信号来保存信息的，不存在机器操作，所以访问速度非常快，具体的访问原理可以查看CSAPP，另外，他们是易失的，即如果断电，保存DRAM和SRAM保存的信息就会丢失。
我们使用的更多的是使用磁盘，磁盘能够保存大量的数据，从GB一直到TB级，但是他的读取速度比较慢，因为涉及到机器操作，读取速度为毫秒级，从DRAM读速度比从磁盘度快10万倍，从SRAM读速度比从磁盘读快100万倍。下面来看下磁盘的结构：
如上图，磁盘由盘片构成,每个盘片有两面，又称为盘面(Surface)，这些盘面覆盖有磁性材料。盘片中央有一个可以旋转的主轴(spindle)，他使得盘片以固定的旋转速率旋转，通常是5400转每分钟(Revolution Per Minute,RPM)或者是7200RPM。磁盘包含一个多多个这样的盘片并封装在一个密封的容器内。上图左，展示了一个典型的磁盘表面结构。每个表面是由一组成为磁道(track)的同心圆组成的，每个磁道被划分为了一组扇区(sector).每个扇区包含相等数量的数据位，通常是（512）子节。扇区之间由一些间隔(gap)隔开,不存储数据。
以上是磁盘的物理结构，现在来看下磁盘的读写操作：
如上图，磁盘用读/写头来读写存储在磁性表面的位，而读写头连接到一个传动臂的一端。通过沿着半径轴前后移动传动臂，驱动器可以将读写头定位到任何磁道上，这称之为寻道操作。一旦定位到磁道后，盘片转动，磁道上的每个位经过磁头时，读写磁头就可以感知到位的值，也可以修改值。对磁盘的访问时间分为 寻道时间，旋转时间，以及传送时间。
由于存储介质的特性，磁盘本身存取就比主存慢很多，再加上机械运动耗费，因此为了提高效率，要尽量减少磁盘I/O，减少读写操作。为了达到这个目的，磁盘往往不是严格按需读取，而是每次都会预读，即使只需要一个字节，磁盘也会从这个位置开始，顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理：
当一个数据被用到时，其附近的数据也通常会马上被使用。
程序运行期间所需要的数据通常比较集中。
由于磁盘顺序读取的效率很高（不需要寻道时间，只需很少的旋转时间），因此对于具有局部性的程序来说，预读可以提高I/O效率。
预读的长度一般为页（page）的整倍数。页是计算机管理存储器的逻辑块，硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块，每个存储块称为一页（在许多操作系统中，页得大小通常为4k），主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时，会触发一个缺页异常，此时系统会向磁盘发出读盘信号，磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中，然后异常返回，程序继续运行。
文件系统及数据库系统的设计者利用了磁盘预读原理，将一个节点的大小设为等于一个页，这样每个节点只需要一次I/O就可以完全载入。为了达到这个目的，在实际实现B-Tree还需要使用如下技巧：
每次新建一个节点的同时，直接申请一个页的空间( 512或者1024)，这样就保证一个节点物理上也存储在一个页里，加之计算机存储分配都是按页对齐的，就实现了一个node只需一次I/O。如，将B树的度M设置为1024，这样在前面的例子中，600亿个元素中只需要小于4次查找即可定位到某一存储位置。
同时在B+树中，内节点只存储导航用到的key，并不存储具体值，这样内节点个数较少，能够全部读取到主存中，外接点存储key及值，并且顺序排列，具有良好的空间局部性。所以B及B+树比较适合与文件系统的数据结构。下面是一颗B树，用来进行内容存储。
另外B/B+树也经常用做数据库的索引，在mysql中的B+树索引构建就采用的这种数据结构，会在后续文章中进行详细介绍.
总结
本文详细介绍了B树、B+树的特征、操作、以及使用场景，参考了很多前人写的博客，希望对大家能有所帮助。
参考博客如下：
B+树详解
B树详解
B树介绍
