矩阵连乘问题

【问题】

给定n个矩阵的链<A1,A2,…,An>，其中A_i与是A_i-1可乘的，矩阵Ai的维数为p_i-1*p_i（1≤i≤n），

如何确定计算矩阵链乘积A1A2…An的计算次序（完全括号化方式），使得依此次序计算矩阵链乘积需要的数乘次数最少。

【算法分析】

将矩阵连乘积A_iA_i-1...A_j简记为A[i:j] ，i≤j  。

考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开，i≤k<j，则其相应完全加括号方式为:

(A_iA_i+1...A_k)(A_k+1A_k+2...A_j)

计算量：A[i:k]的计算量加上A[k+1:j]的计算量，再加上A[i:k]和A[k+1:j]相乘的计算量。

特征：计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。

矩阵连乘计算次序问题的最优解包含着其子问题的最优解，这种性质称为最优子结构性质。

递归式如下：

 

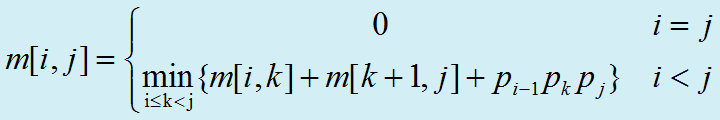
【源代码】

代码（1）

#include <iostream>

using namespace std;

void MatrixChain(int p[], int **m, int **s, int n)
{
    //将对角线元素赋值为零，即单个矩阵计算量为0
    for (int i = 1; i <= n; i++) m[i][i] = 0;
    //r是矩阵相乘个数
    for (int r = 2; r <= n; r++)
        for (int i = 1; i <= n - r+1; i++)
        {
            int j = i + r - 1;
            //计算A[i, j] = A[i: i] A[i+1: j]
            m[i][j] = m[i + 1][j] + p[i-1] * p[i] * p[j];
            s[i][j] = i;  //记下断点i
            for (int k = i + 1; k < j; k++)
            {
                //对i<k<j, 逐个计算A[i, j] = A[i: k] A[k+1: j]
                int t = m[i][k] + m[k + 1][j] + p[i-1] * p[k] * p[j];
                //记下较小的m[i][j]及相应的断点k
                if (t < m[i][j])
                {
                    m[i][j] = t;
                    s[i][j] = k;
                }
            }
        }
}

//找出s数组中记录的最优断开点
void Traceback(int i, int j, int **s)
{
    if (i == j)
    {
        cout << "A" << i;
        return;
    }
    cout << "(";
    Traceback(i, s[i][j], s);
    Traceback(s[i][j] + 1, j, s);
    cout << ")";
}



int main() {
    const int n = 6;
    int p[n + 1] = {30,35,15,5,10,20,25 };
    int **m = new int*[n+1];
    int **s = new int*[n+1];
    for (int i = 0; i < n+1; i++)
    {
        m[i] = new int[n+1];
        s[i] = new int[n+1];
    }

    MatrixChain(p, m, s, n);
    Traceback(1, n, s);

    for (int i = 0; i < n+1; i++)
    {
        delete[] m[i];
        delete[] s[i];
    }
    delete[]m;
    delete[]s;
    return 0;
}

代码（2）

#include <iostream>

using namespace std;

void MatrixChain(int p[], int **m, int **s, int n)
{
    //将对角线元素赋值为零，即单个矩阵计算量为0
    for (int i = 0; i < n; i++) m[i][i] = 0;
    //r是矩阵相乘个数
    for (int r = 2; r <= n; r++)
        for (int i = 0; i <= n - r; i++)
        {
            int j = i + r - 1;
            //计算A[i, j] = A[i: i] A[i+1: j]
            m[i][j] = m[i + 1][j] + p[i] * p[i + 1] * p[j + 1];
            s[i][j] = i;  //记下断点i
            for (int k = i + 1; k < j; k++)
            {
                //对i<k<j, 逐个计算A[i, j] = A[i: k] A[k+1: j]
                int t = m[i][k] + m[k + 1][j] + p[i] * p[k + 1] * p[j + 1];
                //记下较小的m[i][j]及相应的断点k
                if (t < m[i][j])
                {
                    m[i][j] = t;  s[i][j] = k;
                }
            }
        }
}

//找出s数组中记录的最优断开点
void Traceback(int i, int j, int **s)
{
    if (i == j)
    {
        cout << "A" << i + 1;
        return;
    }
    cout << "(";
    Traceback(i, s[i][j], s);
    Traceback(s[i][j] + 1, j, s);
    cout << ")";
}



int main() {
    const int n = 6;
    int p[n + 1] = {30,35,15,5,10,20,25 };
    int **m = new int*[n];
    int **s = new int*[n];
    for (int i = 0; i < n; i++)
    {
        m[i] = new int[n];
        s[i] = new int[n];
    }

    MatrixChain(p, m, s, n);
    Traceback(0, n - 1, s);

    for (int i = 0; i < n; i++)
    {
        delete[] m[i];
        delete[] s[i];
    }
    delete[]m;
    delete[]s;
    return 0;
}

 【算法复杂度分析】

主要计算量取决于算法中对r，i和k的3重循环。
算法的计算时间上界为O(n3)。
算法所占用的空间为O(n2)。