坐标旋转变换公式的推导(转)
翻译自: http://www.metro-hs.ac.jp/rs/sinohara/zahyou_rot/zahyou_rotate.htm
翻译: 汤 永康
出处: http://blog.csdn.net/tangyongkang
转贴请注明出处
1 围绕原点的旋转
如下图, 在2维坐标上,有一点p(x, y) , 直线opの长度为r, 直线op和x轴的正向的夹角为a。 直线op围绕原点做逆时针方向b度的旋转,到达p’ (s,t) 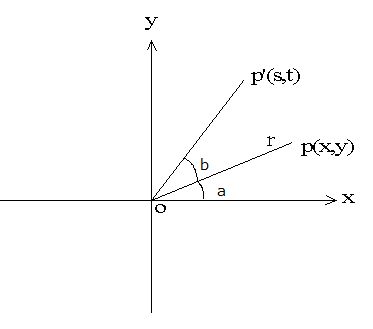
s = r cos(a + b) = r cos(a)cos(b) – r sin(a)sin(b) (1.1)
t = r sin(a + b) = r sin(a)cos(b) + r cos(a) sin(b) (1.2)
其中 x = r cos(a) , y = r sin(a)
代入(1.1), (1.2) ,
s = x cos(b) – y sin(b) (1.3)
t = x sin(b) + y cos(b) (1.4)
用向量和矩阵表达如下:
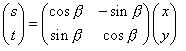
2.坐标系的旋转
在原坐标系xoy中, 绕原点沿逆时针方向旋转theta度, 变成座标系 sot。
设有某点p,在原坐标系中的坐标为 (x, y), 旋转后的新坐标为(s, t)。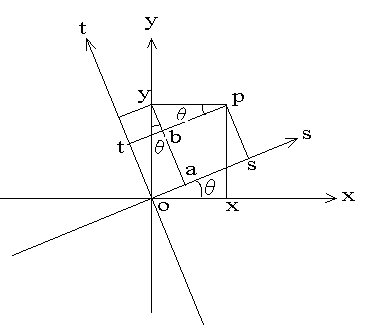
oa = y sin(theta) (2.1)
as = x cos(theta) (2.2)
综合(2.1),(2.2) 2式
s = os = oa + as = x cos(theta) + y sin(theta)
t = ot = ay – by = y cos(theta) – x sin(theta)
用向量和矩阵表达如下:
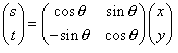



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· 葡萄城 AI 搜索升级:DeepSeek 加持,客户体验更智能
· 什么是nginx的强缓存和协商缓存
· 一文读懂知识蒸馏
2013-12-11 Eclipse设置GC日志输出