原码、反码、补码和移码详解
计算入门
- 原码：正数是其二进制本身；负数是符号位为1,数值部分取X绝对值的二进制。
- 反码：正数的反码和原码相同；负数是符号位为1,其它位是原码取反。
- 补码：正数的补码和原码，反码相同；负数是符号位为1，其它位是原码取反，未位加1。（或者说负数的补码是其绝对值反码未位加1）
- 移码：将符号位取反的补码（不区分正负）
举个例子以一个字节8位说明：
| 编码 | 10810（sbyte） | -10810（sbyte） |
|---|---|---|
| 原码 | 01101100 | 11101100 |
| 反码 | 01101100 | 10010011 |
| 补码 | 01101100 | 10010100 |
| 移码 | 11101100 | 00010100 |
一、为什么需要反码？
反码的作用就相当于数学中的负数。
对于小学生来说，会做的算术题是：5-3，但是不会做3-5。于是，我们上初中的时候，数学里就引进了一个新的概念：负数。引入负数之后，本来是减法的运算就可以变成加法来实现：
3-5=3+[-5]=[-2]，中括号代表“负数”，“负数”就是我们人为给出的数学术语。
对于计算机来说，会做的算术题是：5+3，但是不会做3-5。于是，我们就在编码里引进了一个新的概念：反码。引入反码之后，本来是减法的运算就可以变成加法来实现：
3-5=3+[-5]=[-2]，中括号代表“反码”，“反码”就是我们人为给出的计算机术语。
这里，你一定有一个疑问：为什么计算机只会做5+3，不会做3-5。这是因为在计算机的数字电路中只有加法器，没有所谓的“减法器”。不是说计算机厂商不会设计减法器，因为聪明的人既然发明了方法能够用加法来实现减法操作，那为什么还需要画蛇添足的弄一个减法器？
接着说：那么反码要怎么定义才能实现减法变加法的功能呢？聪明的人想的办法如下：
1.正数的反码保持原码不变：3=[0_0000011]
2.负数除最高位（正负符号位）外，全部取反(0变1,1变0)：-5=1_0000101取反=[1_1111010]
于是3+[-5]=[-2]的计算过程为：
[0_0000011]+[1_1111010]=[1_11111101]
这样，这种反码方法就成功实现了目标！至于为什么，我想只有数学家能给出解释了。
二、为什么需要补码？
都是因为“0”这个特殊数字的存在。
先问你一个问题:0是正数还是负数？你肯定会说：0既不是正数也不是负数，这是我们初中学到的数学知识。这个回答没有问题，所以以后每次碰到0，人们都不会把它当正数或负数。
那么计算机呢？计算机不同于人脑，计算机在碰到任何数字之前只根据最高位的符号位来判断正负性，“0”表示正数,“1”表示负数。
前面我们推论了为何要用反码，那么用8位二进制反码表示的正数范围： +0 —— +127；负数范围： -127 —— -0。但是，其中有两个特殊的编码会出现：
[0_0000000]=+0 （反码）
[1_1111111]=-0 （反码）
其实，+0和-0代表的都是0。这样一来，“0”这个数字在计算机中的编码就不是唯一的了。对于计算机来说，这是绝对不行的，因为任何数字都只能有1个编码。
于是，聪明的人就做了这样一个决定：把0当成正数，也即+0，这样0的编码就变成：0_0000000。那8位二进制表示的正数范围仍然是： +0 —— +127。
但是，对于负数就必须要做调整，也即-0必须要让位---1_1111111这个编码不能表示-0。我们可以把负数整体向后“挪动1位”：只要将8位二进制表示的负数范围从：-127 —— -0变成：-128 —— -1，就能成功解决问题。
那么怎么整体挪动1位呢？方法就是反码+1。{1_1111111}编码就不再表示-0，而变成了-1。顺着推，最小的编码{1_0000000}就是-128。
我们给这个反码+1又人为的取了一个新的名字，叫补码。于是乎，补码的定义如下：
1.正数的补码保持原码不变：3={0_0000011}
2.负数先求反码，然后再加1：-5=[1_1111010]+1={1_1111011}
于是3+{-5}={-2}的计算过程为：
{0_0000011}+{1_1111011}={11111110}
至此，通过补码就成功解决了数字0在计算机中非唯一编码的问题，且也能实现减法变加法。
所以，在计算机的世界里，0是正数。这点和我们学的数学不一样。
{0_1111111}=+127 （补码）
{0_0000000}=+0 （补码）
{1_1111111}=-1 （补码）
{1_0000000}=-128 （补码）
负数最低位
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补+ [1000 0001]补= [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127] == [ [1000 0000]补 , [0111 1111]补 ] == [-27, 27-1]
因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.
三、浮点数的运算
浮点数的表示
所谓浮点数，指的是小数点位置不固定的数，相比整数能够表示更大的范围，其表示格式如下：
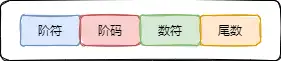
对于一个浮点数 N，我们常用如下形式表示：N = M * Re
- e 叫做 指数（也叫做阶码）；它的位数决定了数值的表示范围，位数越多说明表示的范围越大
- e如果有正负号的话，正负号就叫阶符；
- M为纯小数，叫做尾数；而尾数的位数则决定了数值的有效精度，位数越多说明该数的精度越高。
- 数符，指的是N整个数的符号。
- R 叫做 基数（2进制的话，固定为2）
例如对于一个整数 1000，用浮点数的形式表示即为 1000=1.0∗103，其中 1.0 就对应着浮点数表示形式中的尾数，而 10 则对应着基数，3 则对应着指数。
https://www.jianshu.com/p/abbdae4f3841
https://zhuanlan.zhihu.com/p/105917577
