单源点最短路径的Dijkstra算法
在带权图(网)里,点A到点B所有路径中边的权值之和为最短的那一条路径,称为A,B两点之间的最短路径;并称路径上的第一个顶点为源点(Source),最后一个顶点为终点(Destination)。在无权图中,最短路径则是两点之间经历的边数最少的路径。实际上,只要把无权图上的每条边都看成是权值为1的边,那么无权图和带权图的最短路径是一致的。
给定一个带权有向图G=(V,E),指定图G中的某一个顶点的V为源点,求出从V到其他各顶点之间的最短路径,这个问题称为单源点最短路径问题。
迪杰斯特拉(Dijkstra)根据若按长度递增的次序生成从源点v0到其它顶点的最短路径,则当前正在生成的最短路径上除终点外,其余顶点的最短路径均已生成的这一思想,提出了按路径长度递增的次序产生最短路径的算法(在此,路径长度为路径上边和弧的权值之和)。Dijkstra算法的思想是:对带权有向图G=(V,E),设置两个顶点集合S和T=V-S;凡是以v0为源点并已确定了最短路径的终点(顶点)都并入到集合S,集合S的初态只含有源点v0;而未确定其最短路径的顶点均属于集合T,初态时集合T包含除了源点v0之外的其他顶点。按照各顶点与v0间最短路径的长度递增的次序,逐个把集合T中的各顶点的路径长度。并且,集合S中每加入一个新的顶点u,都要修改源点v0到集合T中剩余顶点的最短路径长度;也即,集合T中各顶点v新的最短路径长度值或是原来最短路径长度值,或是顶点u的最短路径长度值再加上顶点u到顶点v的路径长度值之和这两者中的较小值。这种把集合T中的顶点加入到集合S中的过程不断重复,直到集合T的顶点全部加入到集合S中为止。
Dijkstra算法的实现中,以二维数组gm作为n个顶点带权有向图G=(V,E)的存储结构,并设置一个一维数组s(下标是0~n-1)用来标记集合S中已找到最短路径的顶点,而且规定:如果s[i]为0,则表示未找到源点v0到顶点vi的最短路径,也即此时vi在集合T中;如果s[i]为1,则表示已找到源点v0到顶点vi的最短路径(此时vi在集合S中).除了数组s外,还设置了一个数组dist(下标是0~n-1),用来保存从源点v0到终点vi的当前最短路径的长度.dist的初值为<v0,vi>边上的权值;若v0到vi没有边,则权值为&(无穷)。此后每当有一个新的顶点进入集合S中时,dist[i]值可能被修改变小.一维数组path(下标是0~n-1)用于保存最短路径长度中路径上边所经过的顶点序列;其中,path[i]保存从源点v0到终点vi当前最短路径中前一个顶点编号,它的初值是:如果v0到vi有边则置path[i]为v0的编号;如果v0到vi没有边则置path[i]为-1.
参考代码:
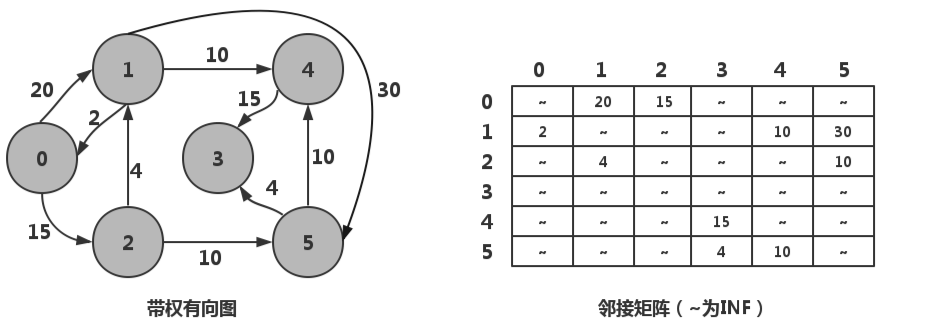
1 #include<stdio.h> 2 #define MAXSIZE 6 3 #define INF 32767 4 5 void Ppath(int path[],int i,int v0)//先序递归查找最短路径(源点为v0)上的顶点 6 { 7 int k; 8 k=path[i]; 9 if(k!=v0)//顶点Vk不是源点V0时 10 { 11 Ppath(path,k,v0);//递归查找顶点Vk的前一个顶点 12 printf("%d,",k);//输出顶点Vk 13 } 14 } 15 16 void Dispath(int dist[],int path[],int s[],int v0,int n)//输出最短路径 17 { 18 int i; 19 for(i=0;i<n;i++) 20 if(s[i]==1)//顶点Vi在集合S中 21 { 22 printf("从%d到%d的最短路径长度为:%d,路径为:",v0,i,dist[i]); 23 printf("%d,",v0);//输出路径上的源点v0; 24 Ppath(path,i,v0);//输出路径上的中间顶点vi 25 printf("%d\n",i);//输出路径上的终点 26 } 27 else 28 printf("从%d到%d不存在路径\n",v0,i); 29 } 30 31 void Dijkstra(int gm[][MAXSIZE],int v0,int n)//Dijkstra算法 32 { 33 int dist[MAXSIZE],path[MAXSIZE],s[MAXSIZE]; 34 int i,j,k,mindis; 35 for(i=0;i<n;i++) 36 { 37 dist[i]=gm[v0][i];//v0到vi的最短路径初值赋给dist[i] 38 s[i]=0;//s[i]=0表示顶点vi属于T集 39 if(gm[v0][i]<INF)//路径初始化,INF为可取的最大常数 40 path[i]=v0; 41 else 42 path[i]=-1;//v0到vi没有边 43 } 44 s[v0]=1;path[v0]=0;//V0并入集合S且V0当前最短路径中无前一个顶点 45 for(i=0;i<n;i++)//对除V0外的n-1个顶点寻找最短路径,即循环n-1次 46 { 47 mindis=INF; 48 for(j=0;j<n;j++)//从当前集合T中选择一个路径长度最短的顶点Vk 49 if(s[j]==0&&dist[j]<mindis) 50 { 51 k=j; 52 mindis=dist[j]; 53 } 54 s[k]=1;//顶点Vk加入集合S中 55 for(j=0;j<n;j++)//调整源点v0到集合T中任一顶点Vj的路径长度 56 if(s[j]==0)//顶点vj在集合T中 57 if(gm[k][j]<INF&&dist[k]+gm[k][j]<dist[j])//当V0到Vj的路径长度小于V0到Vk和Vk到Vj的路径长度时 58 { 59 dist[j]=dist[k]+gm[k][j]; 60 path[j]=k;//Vk是当前最短路径中Vj的前一个顶点 61 } 62 } 63 Dispath(dist,path,s,v0,n);//输出最短路径 64 } 65 66 void main() 67 { 68 int g[MAXSIZE][MAXSIZE]={{INF,20,15,INF,INF,INF},{2,INF,INF,INF,10,30},{INF,4,INF,INF,INF,10}, 69 {INF,INF,INF,INF,INF,INF},{INF,INF,INF,15,INF,INF},{INF,INF,INF,4,10,INF}};//定义邻接矩阵g 70 Dijkstra(g,0,6);//求顶点0的最短路径 71 }
输出: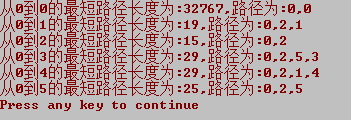
带权有向图及邻接矩阵示意: