01背包

01背包

题目描述：

有N种物品和一个容量为m的背包。每件物品只能使用一次。

第i件物品的体积是v[i]，价值是w[i]。求解将哪些物品装入背包，可使这些物品的体积总和不超过背包容量，且总价值最大。

 

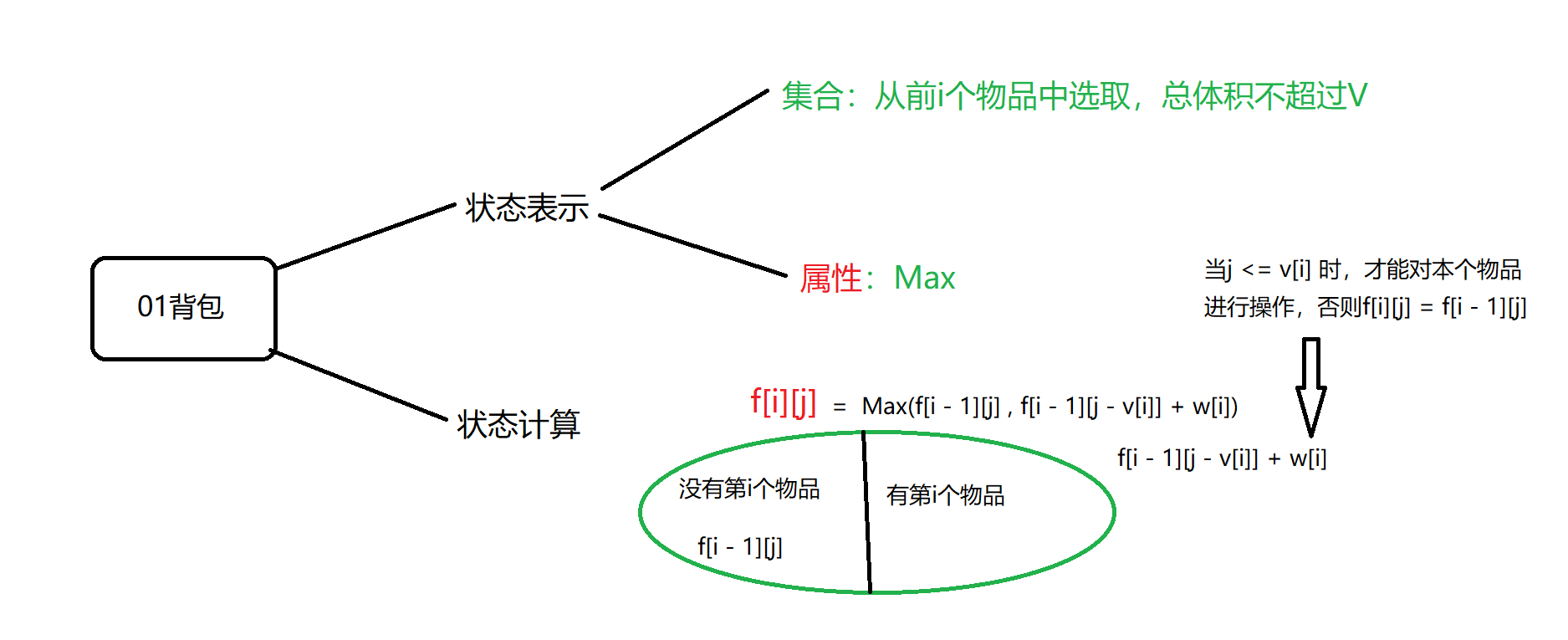
分析：从集合角度对 01 背包问题进行分析，将情况分为含有第i个物品和不含有第i个物品，下面结合代码进行分析：

朴素版01背包代码（二维版本）（这个代码插入还挺帅QAQ）时间复杂度O(n^2)

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[N],w[N];
int n,m;
int f[N][N];              //总价值数组
int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n;i ++)
    cin >> v[i] >> w[i];
    for(int i = 1;i <= n;i ++)  
    for(int j = 0;j <= m;j ++)
    {
        f[i][j] = f[i - 1][j]; //状态一：从前i件物品中取，取件中不包含物品i，总体积不大于j
        if(j >= v[i])
        f[i][j] = max(f[i][j] , f[i - 1][j - v[i]] + w[i]);//状态一二：从前i件物品中取，取件中包含物品i，总体积不大于j
    }
    cout << f[n][m] << endl;//从前n件物品中取物品总体积不超过m的最大价值
    return 0;
}

优化版01背包（一维的船新版本）时间复杂度O（n^2）

优化思想：运用了滚动数组的思想以及逆序遍历（较为重要）

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int n,m;
int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n;i ++)
    cin >> v[i] >> w[i];
    for(int i =1;i <= n;i ++)
    for(int j = m;j >=v[i];j --)         //逆序遍历容量
    f[j] =max(f[j] , f[j - v[i]] + w[i]);//保证此时的f[j - v[i]]的状态为f[i - 1]下的
    cout << f[m] << endl;
    return 0;
}

为了学习方便，整体模拟一遍一维状态下的01背包代码：

样例：  4 5

    1 2

    2 4

    3 4

    4 5

输出：    8

 i = 1时   j >= v[ 1 ] = 1     w[1] = 2

F[ 5 ] = max(F [ 5 ] , F[ 5  -  v [1] ] + w [1] )             F[ 5 ] =F[ 4 ]  + w [ 1 ]  =  2

F[ 4 ] = max(F [ 4 ] , F[ 4  -  v [1] ] + w [1] )             F[ 4 ] =F[ 3 ]  + w [ 1 ]  =  2

F[ 3 ] = max(F [ 3 ] , F[ 3  -  v [1] ] + w [1] )             F[ 3 ] =F[ 2 ]  + w [ 1 ]  =  2

F[ 2 ] = max(F [ 5 ] , F[ 2  -  v [1] ] + w [1] )             F[ 2 ] =F[ 1 ]  + w [ 1 ]  =  2

F[ 1 ] = max(F [ 5 ] , F[ 1  -  v [1] ] + w [1] )             F[ 1 ] =F[ 0 ]  + w [ 1 ]  =  2

 

i = 2 时，j >= v[ 2 ] = 2          w[2] = 4

F[ 5 ] = max(F [ 5 ] , F[ 5  -  v [2] ] + w [2] )            F[ 5 ] =F[ 3 ]  + w [ 2 ]  =  6

F[ 4 ] = max(F [ 4 ] , F[ 4 -  v [2] ] + w [2] )             F[ 4 ] =F[ 2 ]  + w [ 2 ]  =  6

F[ 3 ] = max(F [ 3 ] , F[ 3  -  v [2] ] + w [2] )            F[ 3 ] =F[ 1 ]  + w [ 2 ]  =  6

F[ 2 ] = max(F [ 2 ] , F[ 2  -  v [2] ] + w [2] )            F[ 2 ] =F[ 0 ]  + w [ 2 ]  =  4

 

i = 3 时， j >= v[ 3 ] = 3         w[3] = 4

F[ 5 ] = max(F [ 5 ] , F[ 5  -  v [3] ] + w [3] )           F[ 5 ] =F[ 2 ]  + w [ 3 ]  =  8

F[ 4 ] = max(F [ 4 ] , F[ 4  -  v [3] ] + w [3] )           F[ 4 ] =F[ 1 ]  + w [ 3 ]  =  6

F[ 3 ] = max(F [ 3 ] , F[ 3  -  v [3] ] + w [1] )           F[ 3 ] =F[ 0 ]  + w [ 3 ]  =  4 < 6  则F[ 3 ] = 6

 

i = 4 时， j >= v[4] = 4         w[4] = 5

F[ 5 ] = max(F [ 5 ] , F[ 5  -  v [4] ] + w [4] )        F[ 5 ] =F[ 1 ]  + w [ 4 ]  =  7 < 8 则F[ 5 ] = 8

F[ 4 ] = max(F [ 4 ] , F[ 4  -  v [4] ] + w [4] )        F[ 4 ] =F[ 0 ]  + w [ 4 ]  =  5 < 6 则F[ 4 ] = 6

强调：滚动数组主要体现在层次之间存在依赖关系，01背包要求容量维度要从大到小遍历，否则会出现错乱现象，下面将举例分析

逆序遍历主要保证本层中F[ j - v[ i ]] + w[ i ]   的层数为i - 1

若为正序，例子中会先算出F[ 2 ]此时层数为 i   ，计算F [ 4 ] 时需用到 i  - 1  层的F[ 2 ]，两者发生冲突

则应采取逆序遍历。

PS：第一次写背包问题的笔记，语言组织一般，哪里若有错误，望聚聚指正。