斐波那契数列递归实现

1.斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家莱昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、55、89……
斐波纳契数列在现代物理、准晶体结构、化学等领域都有直接的应用;为此，美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。
2.我们将该数列中的第n项记为Fib(n),它通过以下递归方式给出：
  Fib(1)=1,Fib(2)=1,Fib(n)=Fib(n-1)+Fib(n-2)（n≥2，n∈ N*）

3.Fib(10)的实现如图所示  （任意的n只需改变最后输入的值即可）       

  

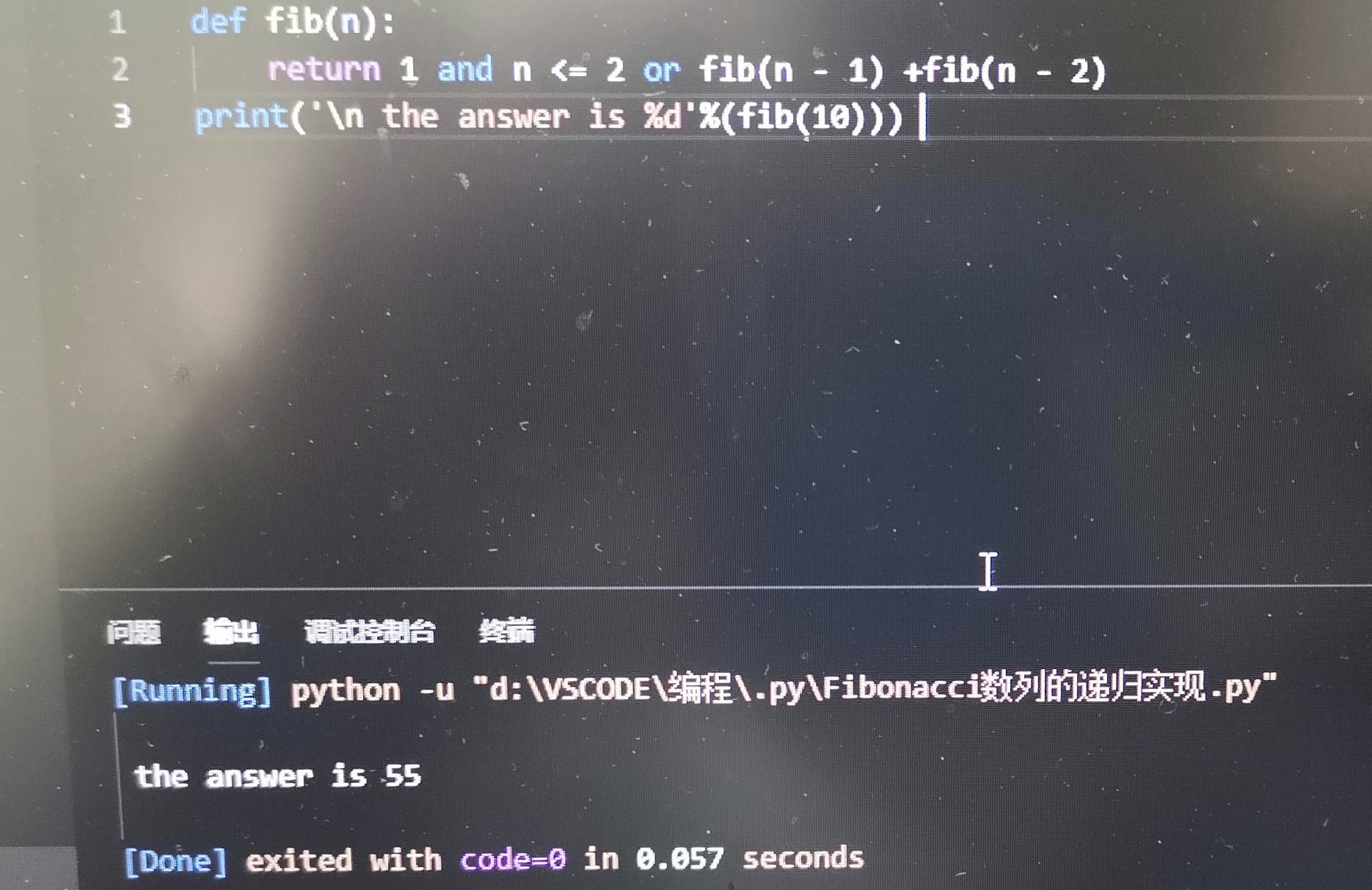
理论上讲，将输入的10改为100、1000、10000即可；但经过测试，Fib(100)已经无法在1分钟内实现，1000、10000就更不必说；

事实证明，递归算法在所求项较大时是难以实现的，故不推荐使用；

附：不如直接使用通项公式Fib(n)={[(1+√5)/2]ⁿ-[(1-√5)/2]ⁿ}/√5,这样对计算机友好一点。