吴恩达机器学习 课时2 模型描述、代价函数和梯度下降的理解
模型描述(Model representation)
让我们通过一个例子来开始:我们使用一个包含俄勒冈州波特兰市房子价格的数据集。根据不同房屋尺寸所售出的价格,在图上进行标注。如果你朋友的房子是1250平方英尺,他想卖掉这栋房子,希望你帮忙估计售出的价格。你可以构建一个模型,在这里可以用条直线模拟,从这个模型上来看,他的房子大概能卖出220000美元左右。这个例子是监督学习算法的一个例子。同时这个问题也可以被称为回归问题。
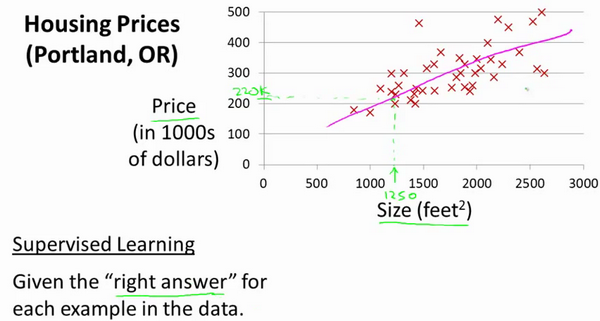
在这个例子中,已知的房子尺寸和他们对应的出售价格被称为训练集(Training Set)。在以后的学习中,我们将用\(m\)表示训练样本的数目。
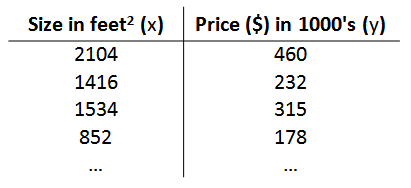
我们将要用来描述这个回归问题的标记如下:
\(m\)代表训练集中实例的数量
\(x\)代表特征/输入变量
\(y\)代表目标变量/输出变量
\((x,y)\)代表训练集中的实例
\((x^{(i)},y^{(i)})\)代表第\(i\)个观察实例
我们来看看监督学习是如何进行工作的,首先将一个数据集提供给学习算法,学习算法的任务是输出一个函数,通常用\(h\)表示,这个函数被称为假设函数(hypothesis function)。他的作用是将房子的大小作为输入变量\(x\),然后输出对应的预测值\(y\)。
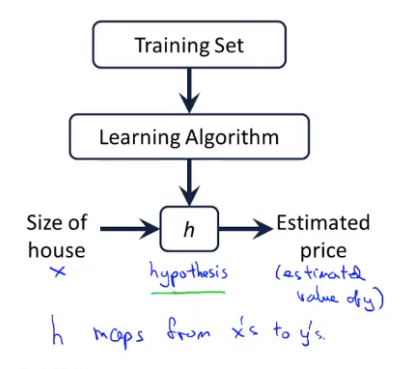
下一步我们要做的就是找到这个假设函数\(h\),在上面的例子中我们可以假设\(h\)为
由于这个函数是线性的,这个问题又是一个回归问题,因此这个模型被称为线性回归,因为在这个函数里面只有一个输入变量\(x\),所以这种问题又被称为单变量线性回归问题。
代价函数(cost function)
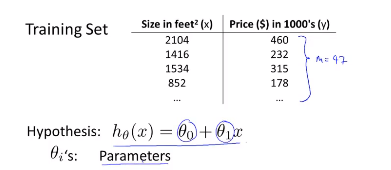
在上面的例子中有如上图的训练集,训练集的样本数量\(m\)=47。
我们的假设函数为:
这些\(\theta_i\)被称为模型参数,不同的\(\theta_0\)和\(\theta_1\)将会产生不同的假设函数。

接下来我们要选择最合适的\(\theta_0\)和\(\theta_1\)使得假设函数的预测值最准确。也就是使得预测值和真实值的差值最小。即得到\(minimize\) \(h_\theta(x) - y\),或者\(minimize\) \((h_\theta(x) - y)^2\)。或许不能对于每一个\((i,j)\)满足\(minimize\) \(h_\theta(x) - y\),但是可以使得所有的\((x,y)\)误差之和满足最小。即\(minimize\) \(\sum_{i = 1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2\)
那么同理,满足\(minimize\) \(
\frac{1}{2m} \sum_{i = 1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2\)即可。
因此我们得到了一个函数
我们称它为代价函数(cost function),当然,代价函数也有很多形式,但是平均损失是在线性回归任务中最常用到的。我们要尽量的减少代价函数的值,所以代价函数又可以被称为优化目标。
代价函数的直观理解Ⅰ
为了能够更加直观的了解什么是代价函数,我们假设\(\theta_0 = 0\),那么假设函数\(h_\theta(x) = \theta_1x\) 也就是一条过圆点的直线,代价函数

所以我们现在的目标就是找到一个合适的\(\theta_1\)来使得\(J(\theta_1)\)最小。
首先我们要明确一点就是\(h_\theta(x)\)和\(J(\theta_1)\)的参数分别是\(x\)和\(\theta_1\)。我们假设我们的数据集为(1,1),(2,2),(3,3)
当我们选择\(\theta_1 = 1\)的时候,假设函数\(h_\theta(x) = x\)刚好是一条通过这三个点的直线。那么将每一个\((h_\theta(x^{(i)}) - y^{(i)})^2\)进行计算后求和得到\(J(1) = 0\),如下图所示。

同理,当我们选择不同的\(\theta_1\)就会得到不同的\(h_\theta(x)\)函数,得到不同的\(J(\theta_1)\)所对应的点,最终我们得到\(J(\theta_1)\)的图像。
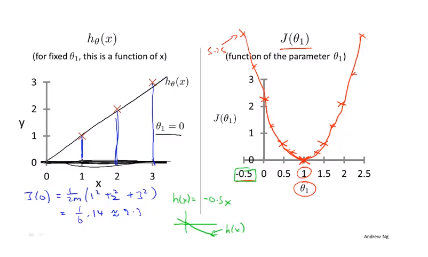
现在我们需要记得学习算法的优化任务就是通过选择不同的\(\theta_1\)得到\(minimize J(\theta_1)\),在\(J(\theta_1)\)曲线上我们可以发现当\(\theta_1 = 1\)时,\(J(\theta_1)\)最小,对应的\(h_\theta(x)\)也最好的贴合数据集。
代价函数的直观理解Ⅱ
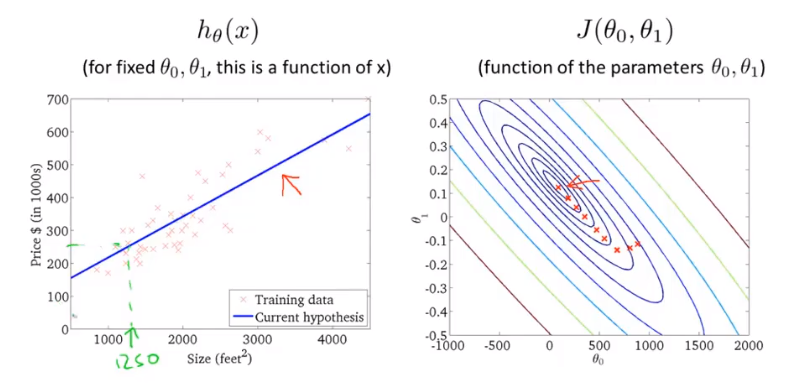
这次我们要同时保留\(\theta_0\)和\(\theta_1\)。假设我们取\(\theta_0 = 50\),\(\theta_1 = 0.06\),得到\(h_\theta(x) = 50 + 0.06x\),它的图像如左图所示,红色x表示我们的数据集。
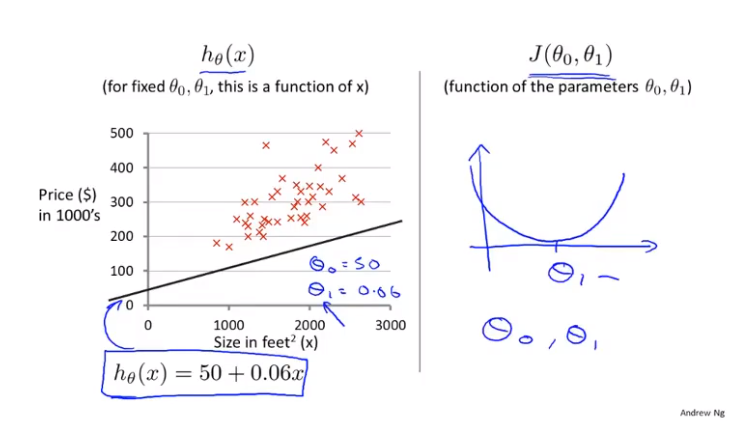
当我们只考虑\(\theta_1\)时得到的图像如上图的右侧所示,这次我们同时保留\(\theta_0\)和\(\theta_1\),代价函数的图像会变得更加复杂。

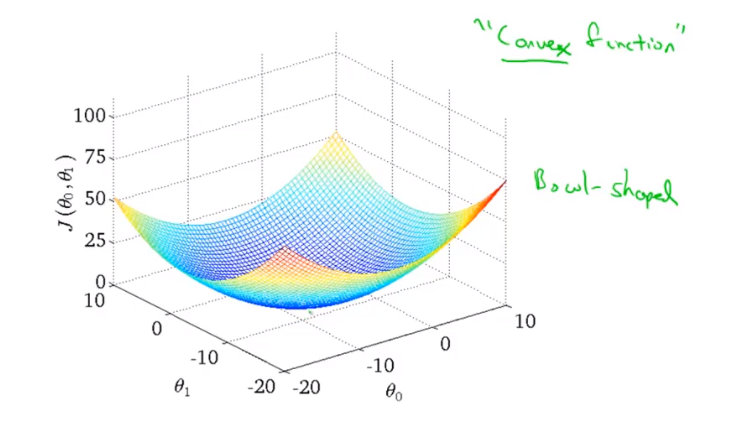
这是一个3维的碗状曲面,横轴表示\(\theta_0\)和\(\theta_1\)。曲面高度便是\(J(\theta_0,\theta_1)\)。在下面的学习中,为了更好的展示图象,我们不再用立体图来表示代价函数而是使用等高线图来表示。
等高线指的是地形图上高程(某点沿铅垂线方向到绝对基面的距离)相等的相邻各点所连成的闭合曲线。
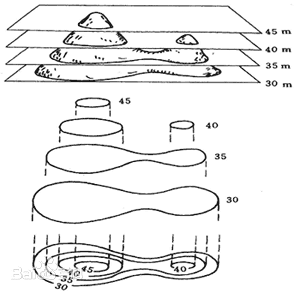
在这里也是一样的概念,即图上同一条线上\(J(\theta_0,\theta_1)\)的值是相同的,例如下面的三个点具有相同的\(J(\theta_0,\theta_1)\)值。
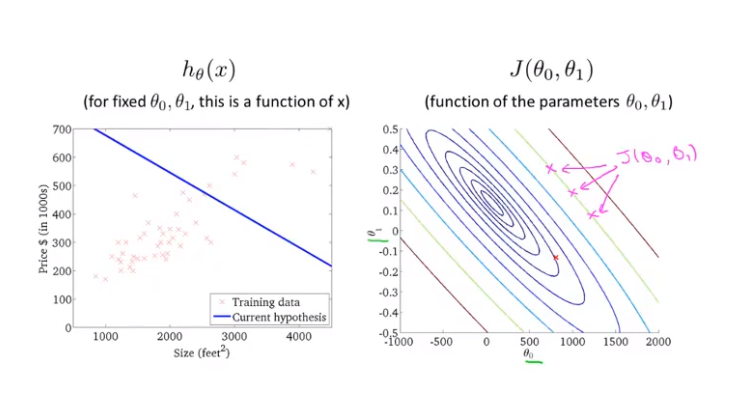
实际上,由于这是一个碗状函数,当我们想象一下这个图的立体图形,就能想象出图像的最低点也就是\(J(\theta_0,\theta_1)\)的最小值在最中间的椭圆上。因此用等高线图来表示\(J(\theta_0,\theta_1)\)更方便。
举个例子,下面的有图中有一点①,它所对应的\(\theta_0 = 800\),\(\theta_1 = -0.15\),\(h_\theta(x)\)所对应的函数如左图。从左图我们可以发现这个假设函数没有很好的拟合曲线,代价值①距离最小值②的距离还非常远。
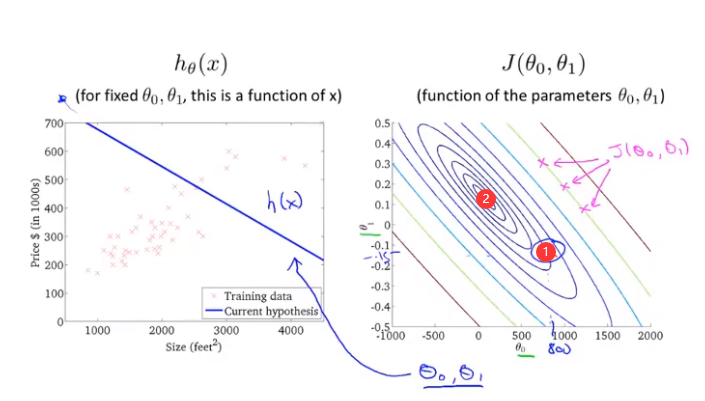
我们再来看另外一个例子,这个例子里面假设函数依然没有很好的拟合数据,但是要比上个例子更好一点。
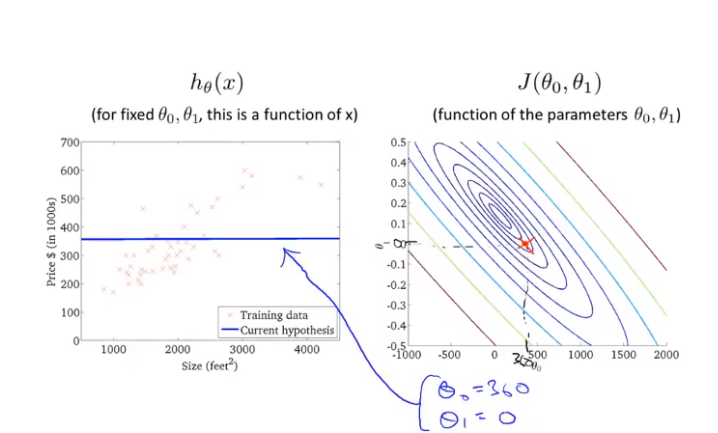
最后这个例子拟合的比较好,但是实际上它也不是最小的代价值。
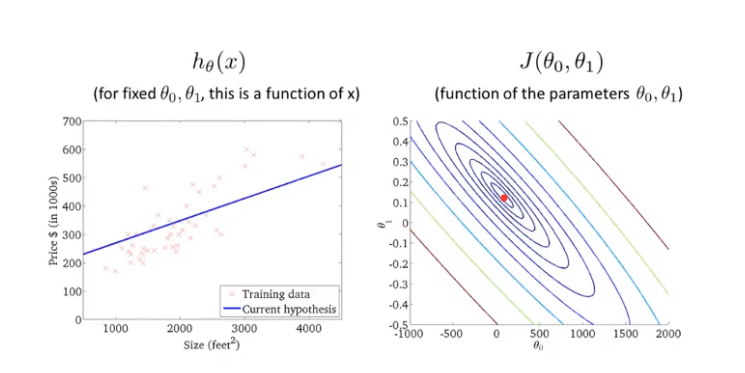
通过以上的例子,我们想说明的是代价函数的意义,以及不同的\(J(\theta_0,\theta_1)\)如何对应着不同的假设函数\(h_\theta(x)\),并且越接近最小代价值的点对应的代价函数能更好的拟合数据。
在上面我们用了几个例子来找到能更好的拟合数据的假设函数\(h_\theta(x)\),然而在实际的操作中我们不可能手动来找到最小的代价值\(J(\theta_0,\theta_1)\)从而得到最佳的假设函数\(h_\theta(x)\),我们下面要学习的梯度下降将帮助我们自动找到\(J(\theta_0,\theta_1)\)的最小值。
梯度下降(Gradient descent)
梯度下降是一个用来求函数最小值的算法,它不仅可以用在线性回归上面还可以用在机器学习众多领域。
我们先将梯度下降应用到任意函数\(J\)上面来体会一下梯度下降的用法,在后面再应用回线性回归。
梯度下降的过程
假设我们有一个函数\(J(\theta_0,\theta_1)\)(实际上这个函数可以是\(J(\theta_0,\theta_1,\theta_2.....\theta_n)\),在这里我们用\(J(\theta_0,\theta_1)\)来简单理解这个过程。)。
我们要做的就是找到一个函数来最小化\(J(\theta_0,\theta_1)\)。
过程:
- 给定\(\theta_0,\theta_1\)的初始值,通常将它们设置为0
- 改变\(\theta_0,\theta_1\)的值,来减少\(J(\theta_0,\theta_1)\)的值,直到找到最小值或者局部最小值

从下面几个图来观测梯度下降如何工作:
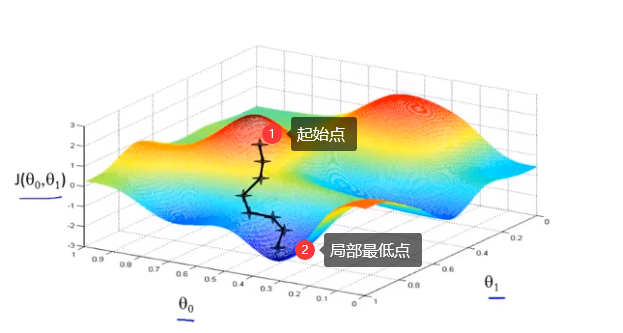
图中,水平坐标分别为\(\theta_0,\theta_1\),垂直坐标为\(J(\theta_0,\theta_1)\),图像表面高度为\(J\)的值。
首先为\(\theta_0,\theta_1\)赋初值,对应图像表面某个点,假设如图上点1。
假设你站在一个如图上所示形状的小山坡,希望尽快下山,那么从点1出发,每一步都会选择下降最快的方向,最后到达局部最低点2。
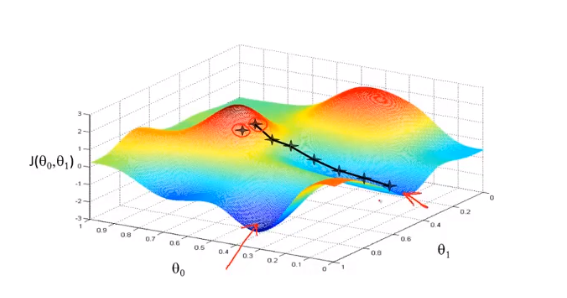
但如果我们的初始位置选择与点1不同,而是选择了相对右边的位置,每一步找到下降最快的方向,重复上述步骤,我们得到的局部最优解将不同于上图。
初始值不同,最终得到的局部最小值可能不同,这也是梯度下降的一个特点。
梯度下降的数学原理:
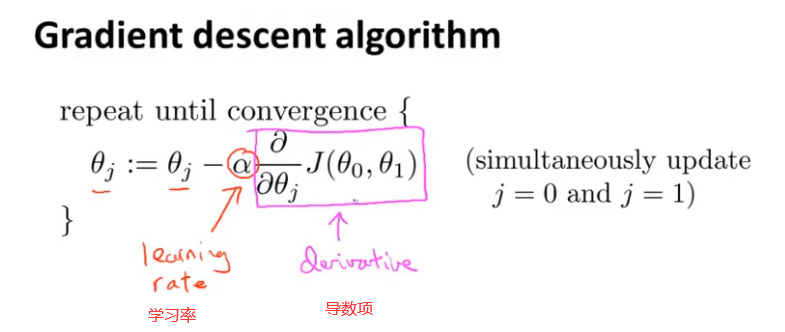
在这里 \(:=\)表示赋值,\(=\)表示真假判断,例如:
\(a:=b\)表示将b的值赋值给a
\(a=b\)表示判断a是否等于b
先将原始的\(\theta_0\)或者\(\theta_1\)代入公式右侧,然后将新的到的\(\theta_0\)或者\(\theta_1\)进行赋值,进行更新。
学习率和导数项的作用:
为了在一维图像上更直观的理解学习率和导数项的作用,我们现在令\(\theta_0\)为0,代价函数为\(J(\theta_1)\)。
导数项的作用:
此时,参数只有\(\theta_1\),因此偏导数\(\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_j}\)变成了导数\(\frac{\mathrm{d}J(\theta_1)}{\mathrm d\theta_1}\)
当初始\(\theta_1\)位于局部最小值右侧是,此时导数\(\frac{\mathrm{d}J(\theta_1)}{\mathrm d\theta_1}\)>0,而学习率\(\alpha>0\)是一定的,因此\(\theta_1\)向左侧移动,直至到达局部最小值点。
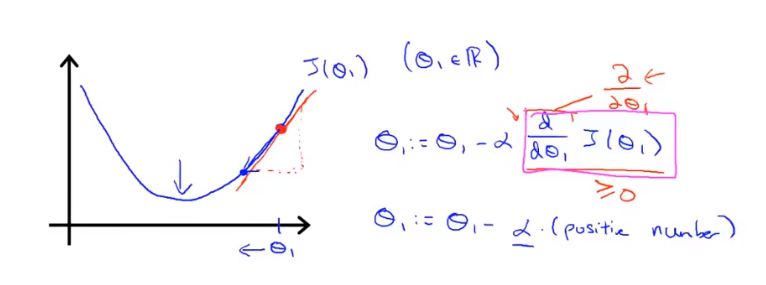
当初始\(\theta_1\)位于局部最小值左侧是,此时导数\(\frac{\mathrm{d}J(\theta_1)}{\mathrm d\theta_1}\)<0,\(\theta_1\)向左侧移动,直至到达局部最小值点。
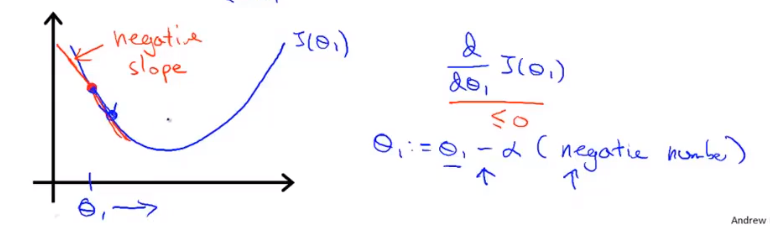
学习率的作用
\(\alpha\) 在这里表示学习率,它用来控制每次下降的“步子”有多大,
\(\alpha\)越大梯度下降的越快。
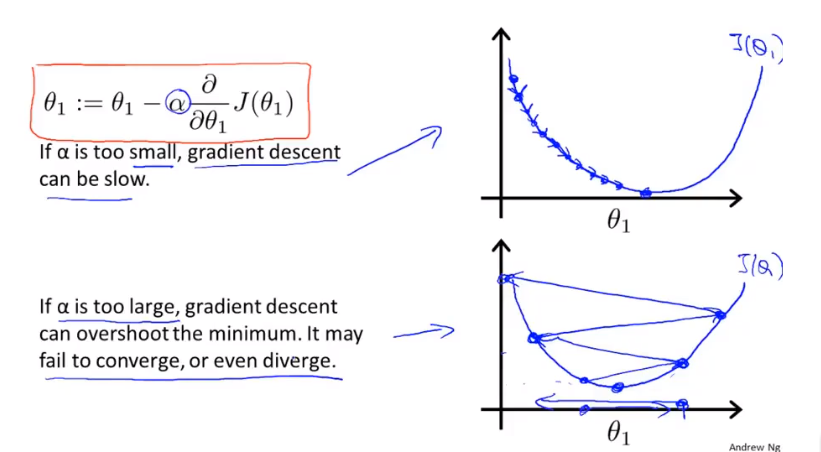
当\(\alpha\)太小时,梯度下降会变的非常缓慢。
当\(\alpha\)太大时,梯度下降可能会跨越最小值点,最终可能无法收敛或者导致发散。
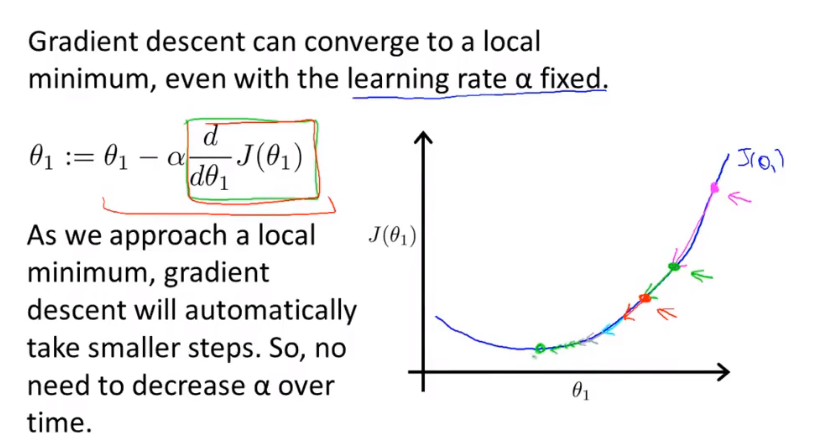
而当起始点已经位于局部最小值点时,导数值为0,此时的\(\theta_1\)值将不再发生变化。

移动过程中有因为图像”坡度“变缓,\(\frac{\mathrm{d}J(\theta_1)}{\mathrm d\theta_1}\)变小,梯度下降会自动变小,因此无需再改变\(\alpha\)的值,最终梯度会下降到达最小值点。
正确的更新顺序
正确的更新顺序应该如下图左所示:

线性回归的梯度下降
左侧是梯度下降算法,右侧是线性回归模型的假设函数\(h_\theta(x)\)和代价函数\(J(\theta_0,\theta_1)\),我们需要所的就是将梯度下降算法应用到代价函数上求得\(minJ(\theta_0,\theta_1)\)。

在梯度下降中,最重要是其导数部分,我们来计算一下这部分的数值:
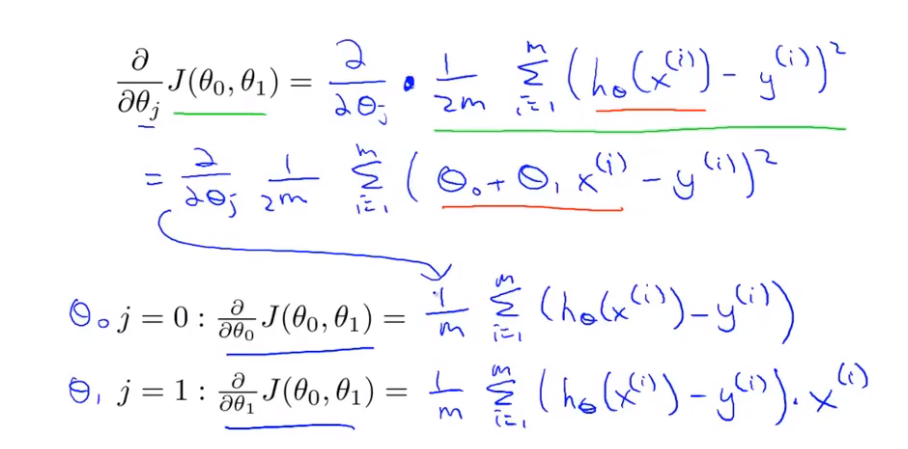
将所得结果带入到梯度下降算法可得:

同时更新\(\theta_0,\theta_1\),直到结果收敛。
从之前的梯度下降算法的示例中我们可以体会到,出师位置的差别将导致收敛的结果不同,且梯度下降容易陷入到局部最优的情况中。
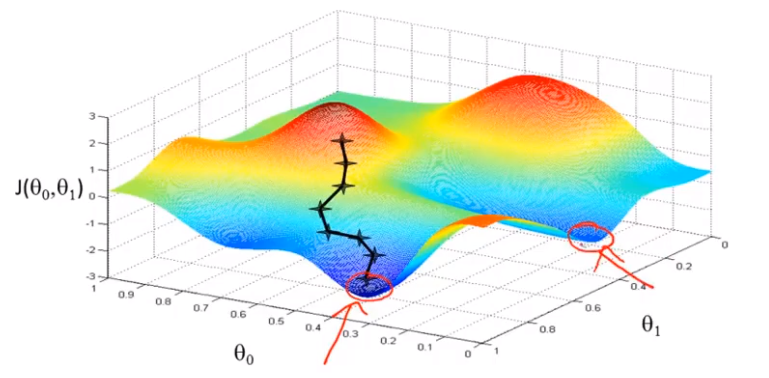
但是我们已知线性回归的代价函数是一个碗装函数,不存在局部最优解,只有全局最优解。
当梯度逐渐下降,对应的假设函数越来越贴合数据,当到达梯度最低点时,得到最优的假设函数\(h(x)\),这就是梯度下降,当我们得到最佳的假设函数时就可以用来进行估测。
在这个梯度下降的算法中,每一次的梯度下降我们都要遍历整个数据集,机器学习中将这种梯度下降方法叫做Batch。以后我们将会学习其他的梯度下降方法。
"Batch"gradient descent
Batch": Each step of gradient descent uses all the training examples

