二叉树基础知识

前言

算法就是一种经常不学就觉得自己是个傻子的存在。所以，复习下吧。

二叉树的基础定义

• 二叉树节点的度：指的是二叉树节点拥有的子节点的数量。
• 二叉树的深度：指的是从根结点开始往下数，叶子节点所在的最大层数。
• 二叉树节点的高度：指的是从当前节点到叶子节点，经过的最短路径的节点数。
• 满二叉树：如果一颗二叉树仅有度为0和度为2的节点，那么称这个二叉树为满二叉树。

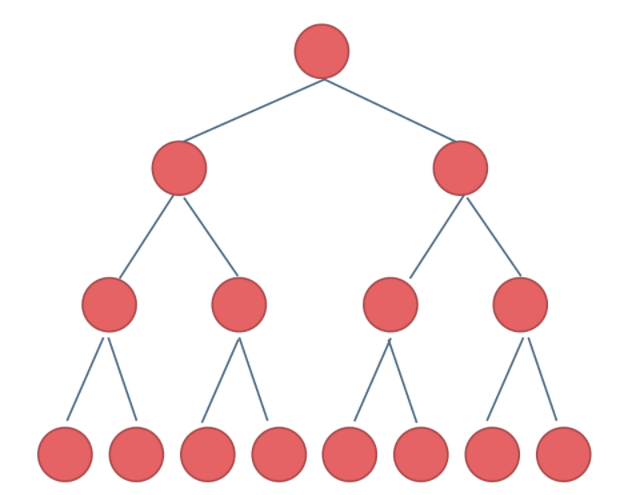
​ 若满二叉树深度为 n ，则其节点数为 2^n - 1.

• 完全二叉树：如果在一颗二叉树中，除了最底层节点外的节点可能没填满外，其余每层节点都达到最大值，且最底层节点都集中在该层最左边的若干位置，那么称这个二叉树为完全二叉树。

  

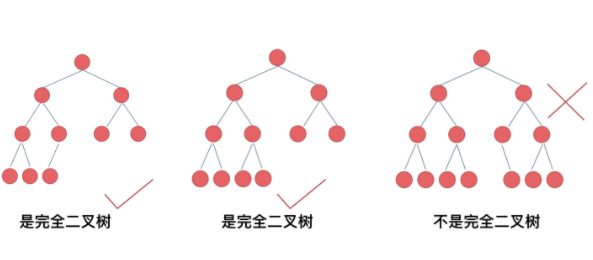
  满二叉树一定是完全二叉树。

• 二叉搜索树：如果在一颗二叉树中，它的非空左子树上所有节点均小于其根节点上的值，且其非空右子树上所有的节点均大于其根节点上的值，且其左右两个子树也都是二叉搜索树，那么称这个二叉树为二叉搜索树。又称二叉排序树、二叉查找树等。

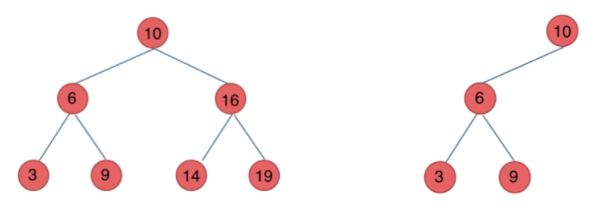
• 平衡二叉树：如果一颗二叉树，它是空树或者它左右两个子树高度差的绝对值不超过1，且其左右两个子树都是平衡二叉树，那么称这个二叉树为平衡二叉树。又称平衡二叉搜索树、二叉平衡树等。

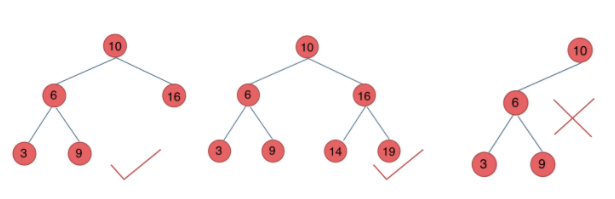
​ 上图中最左边的二叉树不是平衡二叉树，因为其左右子树高度差大于1。

二叉树的存储方式

• 顺序存储。二叉树也可以用数组进行存储。

  

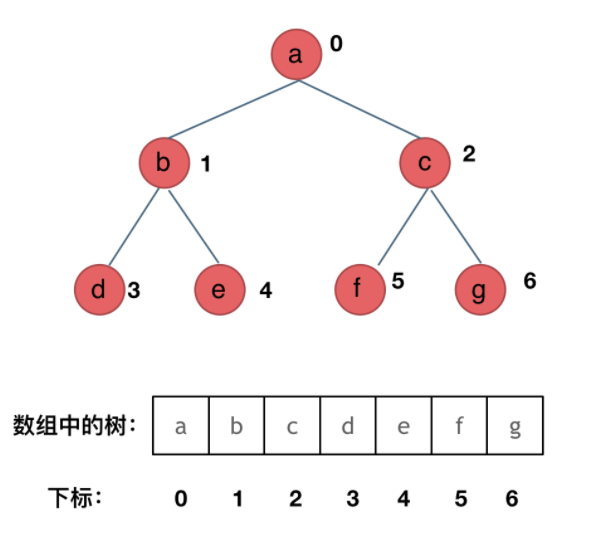
  由上图可知，如果父节点为i，其左子节点为 2 * i + 1，其右子节点为 2 * i + 2。

• 链式存储。这是二叉树最常用的存储方式。

  

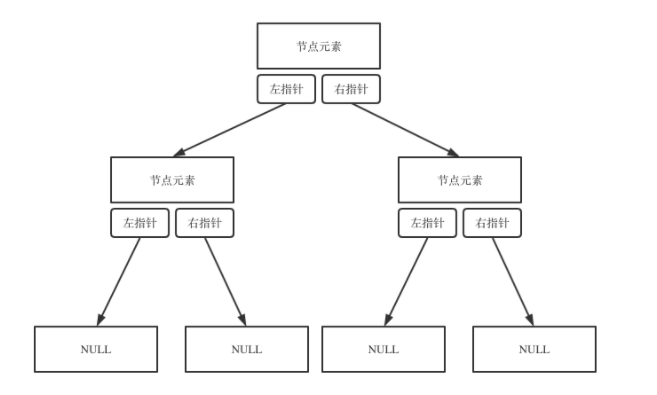
二叉树的遍历方式

• 主要有两种遍历方式：广度优先遍历和深度优先遍历。这两种遍历是图论中最基本的遍历方式。

• 广度优先遍历：主要方法是层序遍历（迭代法）

• 深度优先遍历：主要方法有前序遍历、中序遍历、后续遍历（递归法、迭代法）。这里的前中后指的是中间节点的遍历顺序。

  • 前序遍历：中左右

  • 中序遍历：左中右

  • 后序遍历：右中左

    

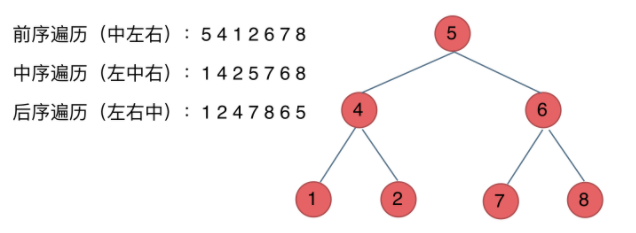
  栈是递归的一种实现结构，深度优先遍历可以借助栈用非递归（迭代）的形式来实现。

  经常使用栈和递归的方式实现深度优先遍历，使用队列和迭代的方式实现广度优先遍历。

二叉树的代码定义

public class TreeNode {
	int val;
	TreeNode left;
	TreeNode right;
	TreeNode() {};
	TreeNode(int val) {
        this.val = val;
    }
	TreeNode(int val, TreeNode left, Tree right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}