一.学习总结
1.1图的思维导图
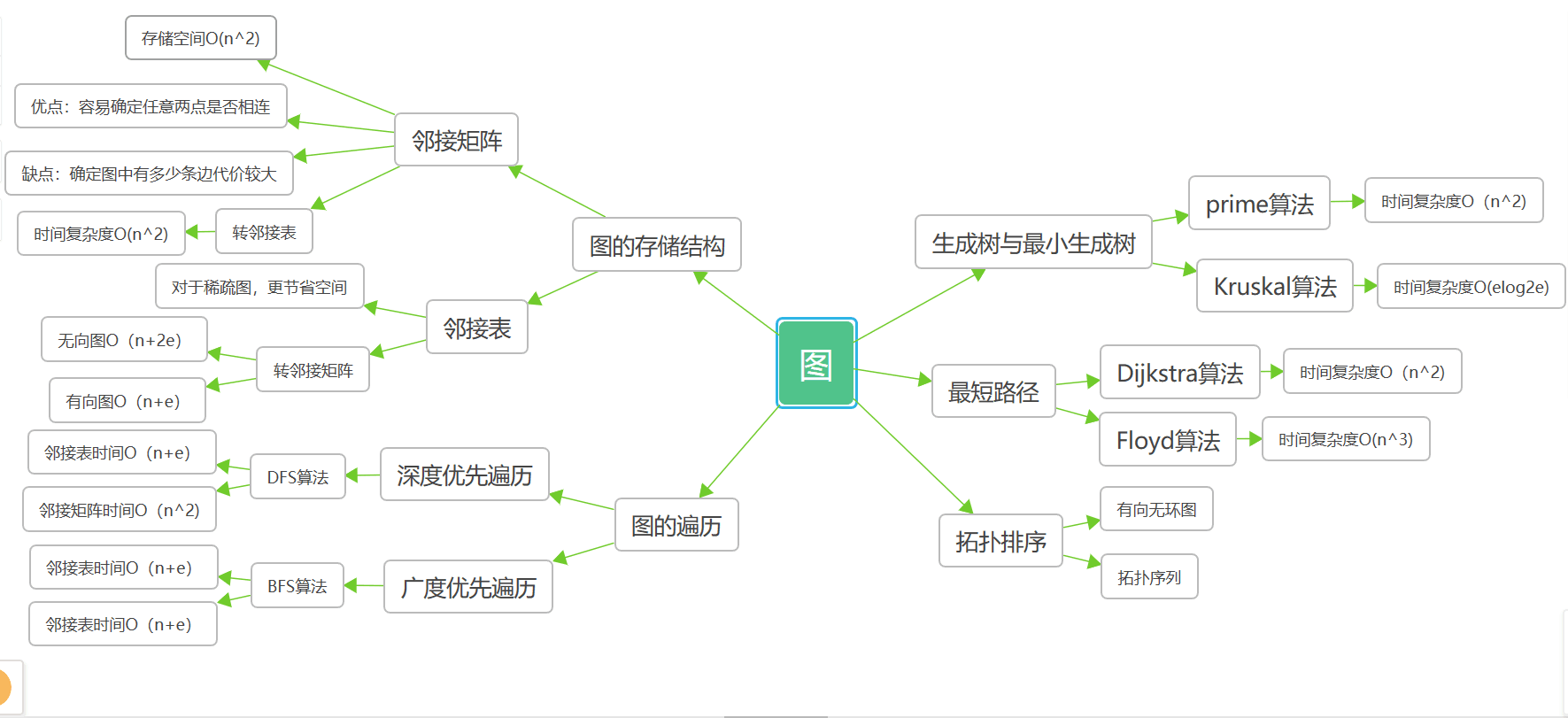
1.2 图结构学习体会
几个经典算法学习体会:
(1)深度遍历算法: 从某个初始顶点出发,选择一个与初始顶点相邻却未被访问的顶点作为下一个初始顶点,再从这个顶点开始深度优先遍历,直到所有顶点都被访问过,这是个递归过程。对于节点之间的连线较少图比较有利。广度优先遍历:需要使用队列,以类似于层次遍历二叉树的方式遍历图。对于节点之间连线较多的图比较有利。总的来说,采用邻接表表示图时时间复杂度都是O(n+e)使用邻接矩阵时间都是O(n^2).
(2)Prim和Kruscal算法:根据Prim算法的特性可以得知,它很适合于点密集的图,一般采用邻接矩阵的存储结构,对于稀疏一点的图,邻接表的存储方式更合适,更节省空间。根据Kruskal算法的特性可得,在边越少的情况下,Kruskal算法相对Prim算法的优势就越大,时间复杂度为O(elog2e),Kruskal算法的速度与点数无关,因此对于稀疏图可以采用Kruskal算法。
(3)Dijkstra算法:在找最短路径的过程中要不断修改最短路径的数值,dist数组内数值的变化时一步一步往下推导的,所以在过程中一旦出现错误,后面的数值也会引发错误。时间复杂度为O(n+e)当顶点和边的数目较多时,时间复杂度较高。
(4)拓扑排序算法:将关系集进行拓扑排序,得出一个线性的序列,则排在前面的任务就是需要先完成的任务。拓扑排序算法在一个有向图无环图里面找一个拓扑序列,拓扑序列并不唯一。
二:PTA实验作业
2.1题目一:六度空间
(1)设计思路:找到一个图中每个节点通过最多5条边能找到的所有节点 ,然后输出百分比。所以需要用广搜记录层数为6以内的所有节点,
1. 引入2个变量 last,tail分别指向当前层数的最后一个元素和下一层的最后一个元素。
2. 若当前出队的元素与last相等则说明即将进入下一层将last更新为tail不停更新tail,直到level = 6 或者队列空。
(2)代码截图:

(3)PTA提交列表说明:
说明:对于二维数组的初始化时只考虑了map[k][l]=1,少写了map[l][k]=1;,
当层数等于6的时候跳出循环而不是5.
前出队的元素与last相等时,层数leve要加一,如果缺少这个if语句,答案错误。
最后输出的时候要控制输出格式。
2.2题目二:图着色问题
(1)设计思路:运用c++函数中verctor容器,放入边与边之间的联系信息方便判断是否相邻。
while(num--){
输入每个方案的颜色排列;
for(i=0;i<v;i++)
for(j=0;j<mp[i].size;j++)
判断该处的color是否和它相邻元素的color相同;
相同则返回false,跳出;}
}循环结束后如果flag标志仍为ture则方案成立。
(2)主要代码截图: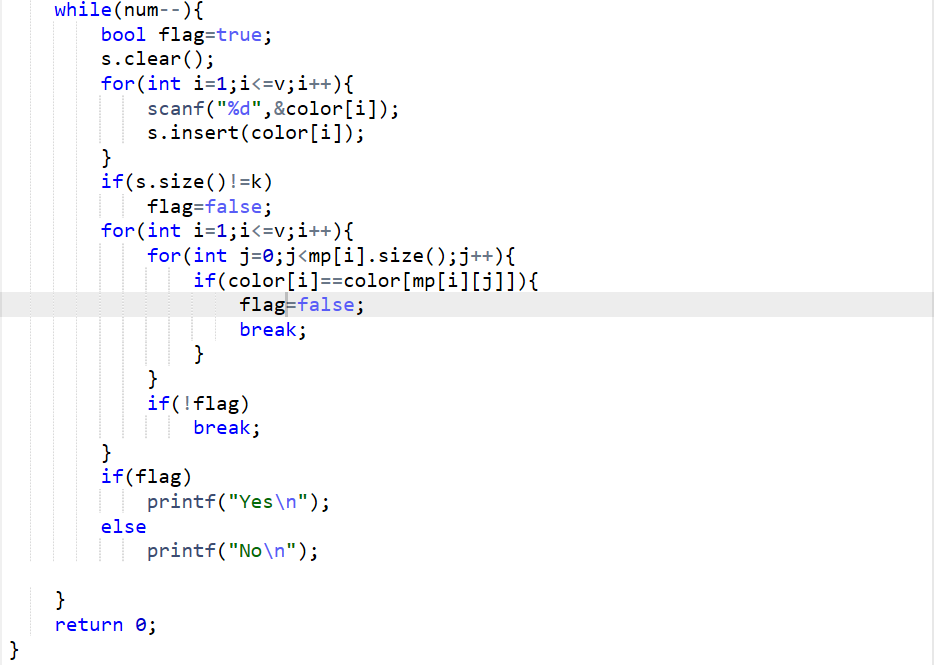
(3)PTA提交列表说明:
说明:一开始段错误时,我使用了邻接矩阵的存储方式,将图内相邻的边用flag=1表示,但如果运用数组给每个顶点附上颜色,相邻边颜色是否相同我无法实现,所以就换成C++内的vector<int>mp[501],运用mp数组可以将某个顶点i的相邻顶点mp[i][j]表示出来,从而来判断颜色是否相同。
2.3题目三:排座位
(1)设计思路:这是一道并查集的题目,题目中亲戚关系判定、确定无向连通图的联通子图的个数、查找有无共同朋友就会用到并查集的知识。首先,当两人之间的关系为1时,就可以输出No problem,当两人之间为-1时,就需要查找两人之间有无共同朋友,从而判定输出的形式。
(2)主要代码截图:
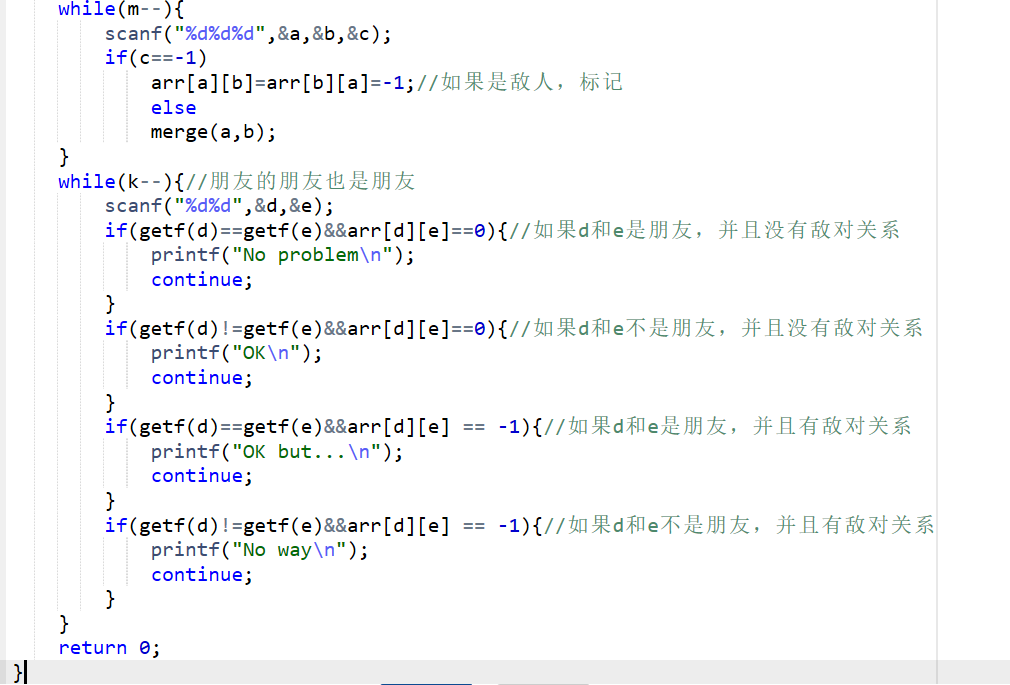
(3)PTA提交说明:
说明:如果是敌人的话要进行标记,但如果不是敌人,仍要执行merge函数,并查集进行合并,朋友的朋友也是朋友。
在关系为-1时,要分四种情况,朋友关系和敌对关系要并列判断。
三:截图本周题目集的PTA最后排名

四:阅读代码
图的迷宫问题:
#include <stdio.h>
#include <malloc.h>
#define MaxSize 100
#define M 4
#define N 4
//以下定义邻接表类型
typedef struct ANode //边的结点结构类型
{
int i,j; //该边的终点位置(i,j)
struct ANode *nextarc; //指向下一条边的指针
} ArcNode;
typedef struct Vnode //邻接表头结点的类型
{
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct
{
VNode adjlist[M+2][N+2]; //邻接表头节点数组
} ALGraph; //图的邻接表类型
typedef struct
{
int i; //当前方块的行号
int j; //当前方块的列号
} Box;
typedef struct
{
Box data[MaxSize];
int length; //路径长度
} PathType; //定义路径类型
int visited[M+2][N+2]= {0};
int count=0;
void CreateList(ALGraph *&G,int mg[][N+2])
//建立迷宫数组对应的邻接表G
{
int i,j,i1,j1,di;
ArcNode *p;
G=(ALGraph *)malloc(sizeof(ALGraph));
for (i=0; i<M+2; i++) //给邻接表中所有头节点的指针域置初值
for (j=0; j<N+2; j++)
G->adjlist[i][j].firstarc=NULL;
for (i=1; i<=M; i++) //检查mg中每个元素
for (j=1; j<=N; j++)
if (mg[i][j]==0)
{
di=0;
while (di<4)
{
switch(di)
{
case 0:
i1=i-1;
j1=j;
break;
case 1:
i1=i;
j1=j+1;
break;
case 2:
i1=i+1;
j1=j;
break;
case 3:
i1=i, j1=j-1;
break;
}
if (mg[i1][j1]==0) //(i1,j1)为可走方块
{
p=(ArcNode *)malloc(sizeof(ArcNode)); //创建一个节点*p
p->i=i1;
p->j=j1;
p->nextarc=G->adjlist[i][j].firstarc; //将*p节点链到链表后
G->adjlist[i][j].firstarc=p;
}
di++;
}
}
}
//输出邻接表G
void DispAdj(ALGraph *G)
{
int i,j;
ArcNode *p;
for (i=0; i<M+2; i++)
for (j=0; j<N+2; j++)
{
printf(" [%d,%d]: ",i,j);
p=G->adjlist[i][j].firstarc;
while (p!=NULL)
{
printf("(%d,%d) ",p->i,p->j);
p=p->nextarc;
}
printf("\n");
}
}
void FindPath(ALGraph *G,int xi,int yi,int xe,int ye,PathType path)
{
ArcNode *p;
visited[xi][yi]=1; //置已访问标记
path.data[path.length].i=xi;
path.data[path.length].j=yi;
path.length++;
if (xi==xe && yi==ye)
{
printf(" 迷宫路径%d: ",++count);
for (int k=0; k<path.length; k++)
printf("(%d,%d) ",path.data[k].i,path.data[k].j);
printf("\n");
}
p=G->adjlist[xi][yi].firstarc; //p指向顶点v的第一条边顶点
while (p!=NULL)
{
if (visited[p->i][p->j]==0) //若(p->i,p->j)方块未访问,递归访问它
FindPath(G,p->i,p->j,xe,ye,path);
p=p->nextarc; //p指向顶点v的下一条边顶点
}
visited[xi][yi]=0;
}
int main()
{
ALGraph *G;
int mg[M+2][N+2]= //迷宫数组
{
{1,1,1,1,1,1},
{1,0,0,0,1,1},
{1,0,1,0,0,1},
{1,0,0,0,1,1},
{1,1,0,0,0,1},
{1,1,1,1,1,1}
};
CreateList(G,mg);
printf("迷宫对应的邻接表:\n");
DispAdj(G); //输出邻接表
PathType path;
path.length=0;
printf("所有的迷宫路径:\n");
FindPath(G,1,1,M,N,path);
return 0;
}





