计数问题专题
鉴于我之前每次考试计数问题都会错一大堆, 所以我滚过来写总结了
先膜拜贡献了这个题单的@feecle6418
以下题目笔者没有事先做过, 和大家一起做, 所以会有一些不成熟的思路, 但是同时也会更好的展示思维路径.
我们先来看几道题来醒醒脑子
洛谷 P6146 Help Yourself G
题意简述:
现在有
(可能不清楚, 左边题目右边博客效果更佳)
首先一个很典的设计是令 我也知道要转移啊
我们思考, 什么时候新加入的这个线段会对答案产生贡献.
思考一下, 一会儿再看答案
首先, 每一个之前的方案都会和这个产生一个组合, ans翻倍
没错, 就是当一个方案与这个线段没有交点的时候.
我们去统计在这之前和自己没有交集的线段数目, 那么这个线段对答案额外贡献就是
(每个都可以选或不选, 都不选也是一种方案)
那么我们先将线段离散, 然后线段树维护即可.
具体的, 我们先把所有的线段按照左端点排序, 然后我们只需要统计右端点小于自己的即可.
还有一个错误的思路是和自己不重叠的要么右端点小于自己的左端点, 要么左端点大于自己的右端点, 维护两个即可. (我WA了, 这个结论的正确性应该是有问题的, 但是我不知道在哪, 求大佬%%%)
时间复杂度
代码:
//start at 15:38
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll MAXN = 2e5 + 10;
const ll MOD = 1e9 + 7;
ll N;
struct xd{
int l, r;
}xs[MAXN];
ll qp(ll d, ll c){
//cerr << d << " " << c << "\n";
ll ans = 1;
while(c){
if(c & 1) ans = (ans * d) % MOD;
d = (d * d) % MOD;
c >>= 1;
}
return ans;
}
ll t[MAXN][3];
inline ll lowbit(ll x){return x & -x;}
inline void add(ll p, ll v, ll f){
for(; p <= 2 * N; p += lowbit(p)) t[p][f] += v;
}
inline ll fin(ll p, ll f){
if(p <= 0) return 0;
ll sum = 0;
for(; p; p -= lowbit(p)) sum += t[p][f];
return sum;
}
inline ll fi(ll l, ll r, ll f){ return fin(r, f) - fin(l - 1, f);}
ll ans;
bool cmp(xd a, xd b){return a.l < b.l;}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin >> N;
for(int i = 1; i <= N; i++) cin >> xs[i].l >> xs[i].r;
sort(xs + 1, xs + N + 1, cmp);
for(int i = 1; i <= N; i++){
ll n = fi(1, xs[i].l - 1, 1);
//cerr << n << "\n";
//cerr << n << " " << fi(1, l[i] - 1, 2) << " " << fi(r[i] + 1, 2 * N, 1) << "\n";
ans = (ans * 2 + qp(2, n)) % MOD;
add(xs[i].r, 1, 1);
}
cout << ans << "\n";
}
//end at 16:06
推题+代码将近大半个小时, 还是太菜了
洛谷P6075 [JSOI2015] 子集选取
题意简述:
有
要求从
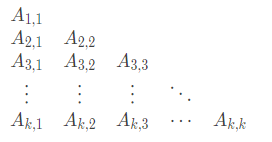
要求
求方案数.
我们关注到复杂度要求是
所以直接盲猜快速幂然后A了
不至于, 但是这道题给我们一个启发, 就是可以去打指数级的暴力(在组合数学题目中一般还是比较好打), 然后去找规律, 一般可能会是
一类的, 我们肉眼看不出来的时候甚至可以枚举
一个小优化:我们知道
不知道的自己去复习费马小定理
所以我们可以把
当然你要用int128我也拦不住你
小Tips: 一般不给样例的题目都会非常结论, 打个暴力你和AC就不远了O
正确性? OI嘛, 大胆猜想, 无需证明!
(逃)
正确的题解在这里
现在进入复杂一点的计数: Polya !
我们先了解一下什么是Polya
作者去学习了, 应该不会回来
这个东西太难了我不会更讲不了所以直接跑路
noip完了踹我我回来填坑




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人