邻接表的广度优先遍历(java版)

 

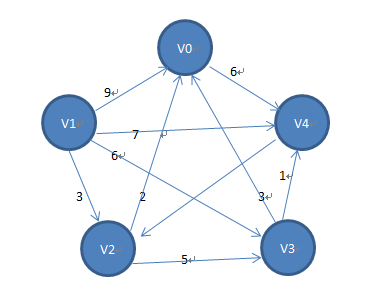
这是一个有向带权的图

1 到 0 的权是 9
1 到 2 的权是 3
1 到 3 的权是 6
1 到 4 的权是 7

2 到 0 的权是 2
2 到 3 的权是 5

3 到 0 的权是 3
3 到 4 的权是 1

4 到 2 的权是 2

0 到 4 的权是 6

遍历思路：
线性数组存放着[v0,v1,v2,v3,v4]
从0号元素开始 i=0；
打印出v0，0入队
0出队，去查找v0的邻接表，找到了v4
打印出v4，4入队
4出队，去查找v4的邻接表，找到了v2
打印出v2，2入队
2出队，去查找v2的邻接表，找到了v0，v3，因为v0是已访问过的
打印出v3，3入队
3出队，去查找v3的邻接表，找到了v0，因为v0是已访问过的
所以此时队列为空，进入下一次循环，i=1；
打印出v1，1入队，接着1出队找邻接表，发现都是已访问过的，队列又为空，进入下一次循环，i=2，直到循环结束

打印顺序是 v0 v4 v2 v3 v1

 

 

package com.datastruct;

import java.util.LinkedList;
import java.util.Scanner;

public class AlGraph {
    
    //边表节点
    private static class EdgeNode{
        int adjvex; //存储该顶点对应的下标
        int weight;
        EdgeNode next;
    }
    
    //顶点表结点
    private static class VertexNode{
        String data; //顶点信息
        EdgeNode firstedge; //边表头指针
    }
    //图结构
    private static class GraphAdjList{
        
        final int MAXVEX = 20;
        VertexNode adjList[] = new VertexNode[MAXVEX]; // 顶点数组
        int numVertexes; // 顶点数
        int numEdges; // 边数
        
        public GraphAdjList(){
             //adjList尽管有的实例，但其元素都是null，需要为每个元素都申请一个VertexNode的实例 ,不然会空指针异常
            for(int i=0;i<MAXVEX;i++){
                
                adjList[i] = new VertexNode();
            }
        }
    }
    
    public static void createAlGraph(GraphAdjList g){
        int i,j,k,w;
        EdgeNode e;
        Scanner scanner = new Scanner(System.in);
        
        System.out.println("输入顶点数和边数：");
        g.numVertexes = scanner.nextInt();
        g.numEdges = scanner.nextInt();
        //录入所有顶点信息
        System.out.println("输入所有顶点信息：");
        for(i=0;i<g.numVertexes;i++){
            g.adjList[i].data = scanner.next();
            g.adjList[i].firstedge = null;
        }
        
        //录入边信息
        for(k=0;k<g.numEdges;k++){
            System.out.println("输入顶点vi,vj及两个点之间的权w");
            i = scanner.nextInt();
            j = scanner.nextInt();
            w = scanner.nextInt();
            
            e = new EdgeNode();
            e.adjvex = j;
            e.weight = w;
            //g.adjList[i].firstedge = e;
            e.next = g.adjList[i].firstedge;//头插法 步骤1
            g.adjList[i].firstedge = e; //头插法 步骤2
            
        }
    }
    
    public static void print(GraphAdjList g){
        int i;
        System.out.println("所有顶点：");
        for(i=0;i<g.numVertexes;i++){
            System.out.print(g.adjList[i].data+" ");
        }
        
        System.out.println();
        System.out.println("每个顶点的链接：");
        for(i=0;i<g.numVertexes;i++){
            
            System.out.print("顶点："+g.adjList[i].data+" ");
            if(null != g.adjList[i].firstedge){
                System.out.print(" 第一个下标： "+g.adjList[i].firstedge.adjvex+" ");
                System.out.print(" 权： "+g.adjList[i].firstedge.weight+" ");
                
                if(null != g.adjList[i].firstedge.next){
                    EdgeNode  e = g.adjList[i].firstedge.next;
                    visit(e);
                }
            }
            System.out.println();
        }
        
    } 
    
    public static void visit(EdgeNode e){
        System.out.print(" 下标： "+e.adjvex+" ");
        System.out.print(" 权："+e.weight+" ");
        if(null != e.next){
            visit(e.next);
        }
    }
    
    
    
    //广度优先遍历
    public static void BFSTraverse(GraphAdjList g){
        boolean visited[] = new boolean[20];
        
        int i;
        EdgeNode p;
        LinkedList queue = new LinkedList();
        for(i=0;i<g.numVertexes;i++){
            visited[i] = false;
        }
        for(i=0;i<g.numVertexes;i++){
            if(!visited[i]){
                visited[i] = true;
                System.out.println(g.adjList[i].data);
                queue.addLast(i);
                while(queue.size() != 0){
                    int index = (int)queue.removeFirst();
                    p = g.adjList[index].firstedge;
                    while(null != p){
                        if(!visited[p.adjvex]){
                            visited[p.adjvex] = true;
                            System.out.println(g.adjList[p.adjvex].data);
                            queue.addLast(p.adjvex);
                        }
                        if(null == p.next){
                            p = null;
                        }else{
                            p = p.next;
                        }
                    }
                }
            }
        }
        
    }
    
    public static void main(String[] args) {
        GraphAdjList g = new GraphAdjList();
        createAlGraph(g);//创建图
        print(g);//打印图的信息
        BFSTraverse(g);//遍历图

    }

}