动态规划--编辑距离算法

设A和B是2个字符串。要用最少的字符操作将字符串A转换为字符串B。这里所说的字符操作包括 (1)删除一个字符； (2)插入一个字符； (3)将一个字符改为另一个字符。 将字符串A变换为字符串B所用的最少字符操作数称为字符串A到 B的编辑距离，记为d(A,B)。 对于给定的字符串A和字符串B，计算其编辑距离 d(A,B)。

 

对于每一个对应字符有三种解决方法案：

 

 

 

 

 

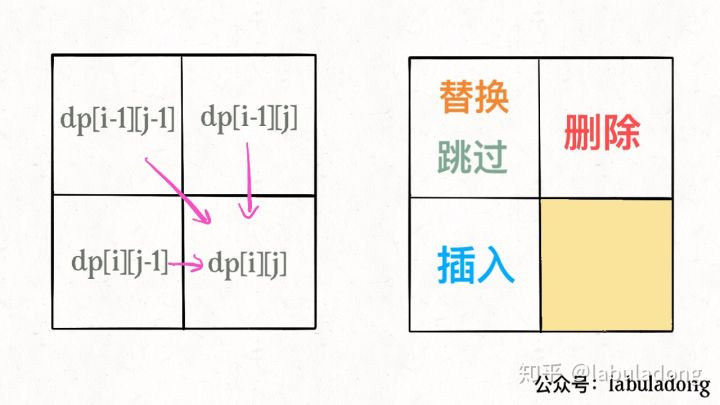
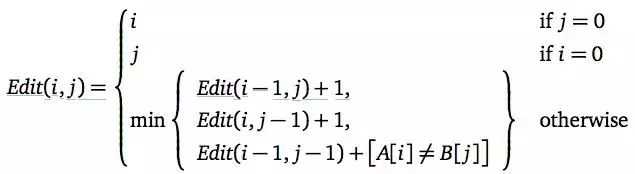
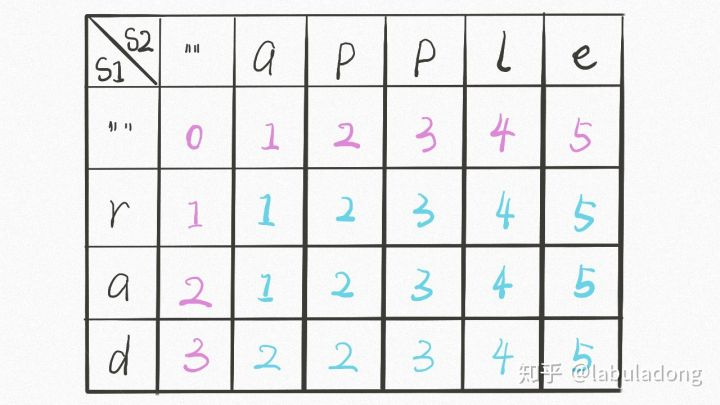
C++代码：

#include <iostream>

#include <string.h>

using namespace std;

int p[2000][2000] = {0};

int min(int a, int b, int c) {

    int cmin = a;

    if (cmin > b)

        cmin = b;

    if (cmin > c)cmin = c;

    return cmin;

}

int main() {

    char a[2000], b[2000];

    cin>>a;

    cin>>b;

    int c = strlen(a), d = strlen(b);

    for (int j = 1; j <= d; j++) {

        p[0][j] = j;

    }

    for (int i = 1; i <= c; i++) {

        p[i][0] = i;

    }

    for (int i = 1; i <= c; i++) {

        for (int j = 1; j <= d; j++) {

 

            if (a[i - 1] == b[j - 1])

                p[i][j] =min(p[i - 1][j]+1, p[i][j - 1]+1, p[i - 1][j - 1]) ;

            else

                p[i][j] =min(p[i - 1][j]+1, p[i][j - 1]+1, p[i - 1][j - 1]+ 1);

        }

    }

cout<<p[c][d];

    return 0;

}