使用matlab仿真 混沌张弛计量经济振荡器 微分方程组

参考文献：https://www.ee.cityu.edu.hk/~gchen/pdf/Rocard.pdf

方程组：

代码如下：

% 混沌张弛计量经济振荡器
% 方程组如下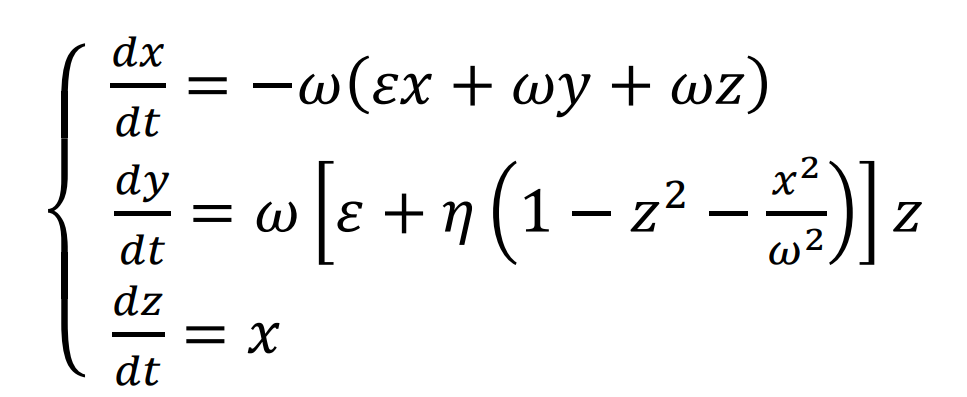  

x0 = 0.1;
y0 = 0.1;
z0 = 0.1;

n = 1e4;
x = zeros(n, 3);
x(1,:) = [x0, y0, z0];

for k=2:n
    [dx,dy,dz] = dxdt_Lorenz(x(k-1,1),x(k-1,2),x(k-1,3));
    x(k,1) = x(k-1,1) + dx;
    x(k,2) = x(k-1,2) + dy;
    x(k,3) = x(k-1,3) + dz;
end
figure;
plot3(x(:,1),x(:,2),x(:,3));
grid on

%%******************************************
% -- 方程组
%%******************************************

function g=f1(x,y,z)
    Omeg = 2;
    ipcl = 0.5;
    g = - Omeg * (ipcl * x + Omeg * y + Omeg * z);
end

function g=f2(x,y,z)
    Omeg = 2;
    ipcl = 0.5;
    eta = 0.1; %[-1.34, 0.94]
    g = Omeg * (ipcl + eta*(1-z*z + x*x/(Omeg*Omeg)))*z;
end

function g=f3(x,y,z)    
    g = x;
end

% ============================================================
% -- 洛伦兹方程的四阶龙格库塔函数
% ============================================================

function [dx,dy,dz] = dxdt_Lorenz(x,y,z)
    h = 1e-2;   %步长

    K1 = f1(x,y,z);
    K2 = f1(x + h*K1/2,y + h*K1/2,z + h*K1/2);
    K3 = f1(x + h*K2/2,y + h*K2/2,z + h*K2/2);
    K4 = f1(x + h*K3,y + h*K3, z + h*K3);

    L1 = f2(x,y,z);
    L2 = f2(x + h*L1/2,y + h*L1/2,z + h*L1/2);
    L3 = f2(x + h*L2/2,y + h*L2/2,z + h*L2/2);
    L4 = f2(x + h*L3,y + h*L3, z + h*L3);

    M1 = f3(x,y,z);
    M2 = f3(x + h*M1/2,y + h*M1/2,z + h*M1/2);
    M3 = f3(x + h*M2/2,y + h*M2/2,z + h*M2/2);
    M4 = f3(x + h*M3,y + h*M3, z + h*M3);

    dx = (K1 + 2*K2 + 2*K3 + K4)*h/6;
    dy = (L1 + 2*L2 + 2*L3 + L4)*h/6;
    dz = (M1 + 2*M2 + 2*M3 + M4)*h/6;
end

结果如下：

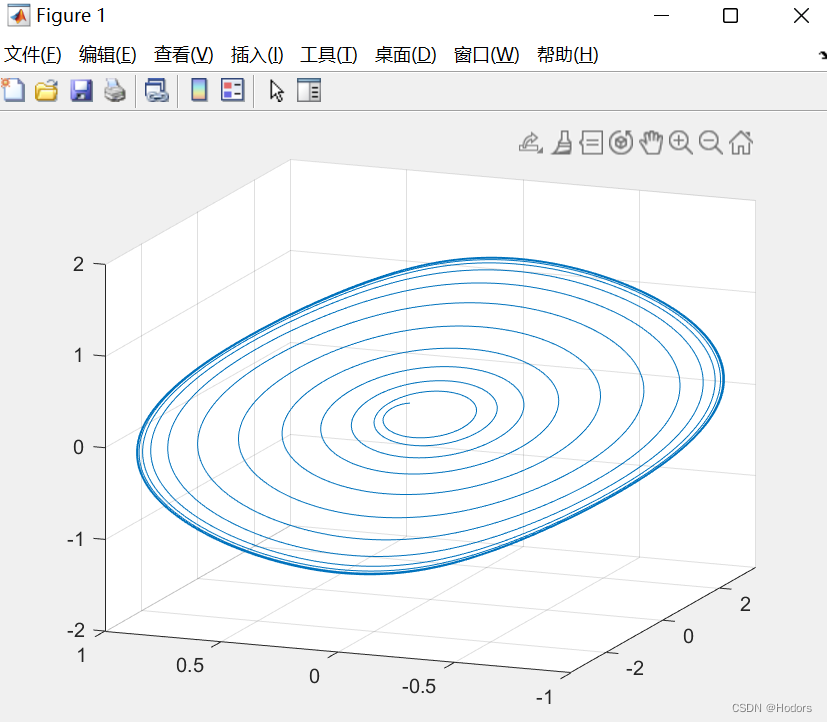
使用matlab仿真 混沌张弛计量经济振荡器