如何理解范德波尔方程

如何理解范德波尔方程

是荷兰物理学家巴尔塔萨·范·德·波尔在1927年发现的真空管放大器的极限环振荡现象[1]。极限环振荡可以用下列非线性微分方程表示：

 

电流随时间的变化，服从一下的规律。

我一直搞不懂，这些一阶，二阶的微分项是怎么来的，以及一阶项为什么还跟x平方有关系。

这是晚上睡觉的时候，上帝告诉他们的吗？

参考资料：

1、

https://www.ee.cityu.edu.hk/~gchen/pdf/Rocard.pdf

2、视频：

https://www.youtube.com/results?search_query=Van+der+Pol

视频：

https://www.youtube.com/watch?v=qaeKi47z4ik&ab_channel=RossDynamicsLab

看了这些内容后，还是无法理出来头绪。

----

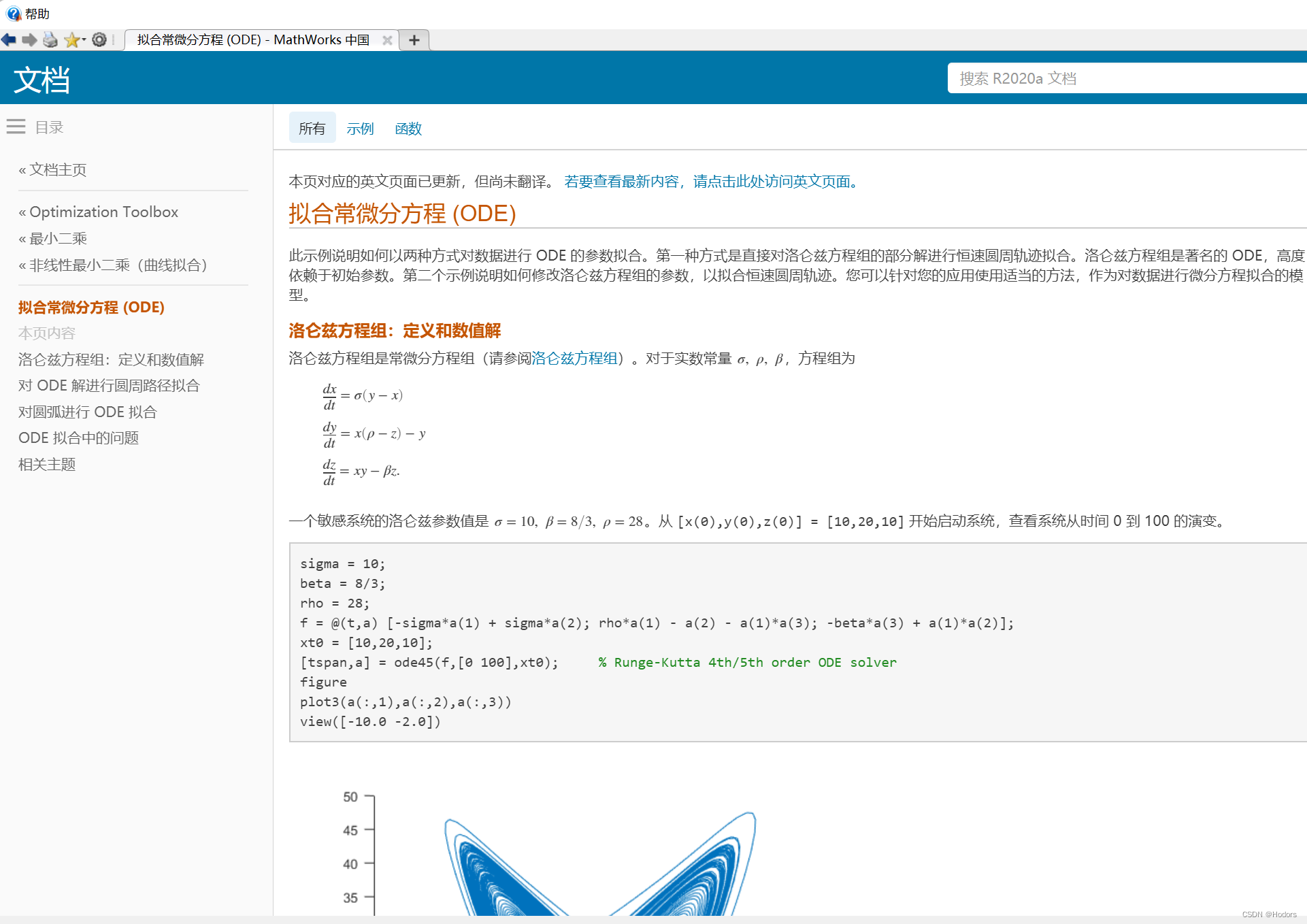
如下图，给出了一个  洛伦兹 混沌系统的微分方程描述，如何绘制其在三维空间中的，坐标轨迹。

 

这里有个线索；

基于matlab的Lorenz系统仿真可视化 - 云+社区 - 腾讯云

将三个微分方程组作为输入，并使用 带有步长的Runge-Kutta方法求解该系统。

matlab 绘 洛伦兹系统 3D相图_颹蕭蕭的博客-CSDN博客_matlab三维相图

这个比上个文献里的内容好。

matlab的官方文档中，有拟合常微分方程的的code

 

 Van der Pol, B., "On relaxation-oscillations", The London, Edinburgh and Dublin Phil. Mag. & J. of Sci., 2(7), 978-992 (1927).
 Richard H. Enns George C. McCGuire, Nonlinear Physics, p35, Birkhauser,1997