范德波尔振荡器 Matlab 或者 Python 仿真。
1、第一步:
范德波尔振荡器 Matlab 或者 Python 仿真。
code:
% 如果有阻尼项,只能通过数值解求得;
% https://ww2.mathworks.cn/help/symbolic/solve-differential-equation-numerically-1.html
% Rewrite the Second-Order ODE as a System of First-Order ODEs
syms y(t);
[V] = odeToVectorField(diff(y, 2) == (1 - y^2)*diff(y) - y);
% Generate MATLAB Function
M = matlabFunction(V,'vars', {'t','Y'});
% Solve the System of First-Order ODEs
sol = ode45(M,[0 20],[2 0]);
% 常见用法:
% [ t , y ] = ode45( odefun , tspan , y0 )
% odefun ,用以表示f(t,y)的函数句柄或inline函数i,t是标量,y是标量或向量;
% tspan 若是二维向量[t0,tf],表示自变量初值t0和终值tf;若是高维向量[t0,t1,...,tn],则表示输出结点列向量;
% y0 初值向量y0;
% t 表示结点列向量(t0,t1,...,tn)^T;
% y 数值解矩阵,每一列对应y的一个分量;
% ode45函数说明:第一个参数是方程的名称,第二个参数是指求解时t的范围,第三组参数是指y中每个元素的初值。
% Plot the Solution
fplot(@(x)deval(sol,x,1), [0, 20]);
结果:
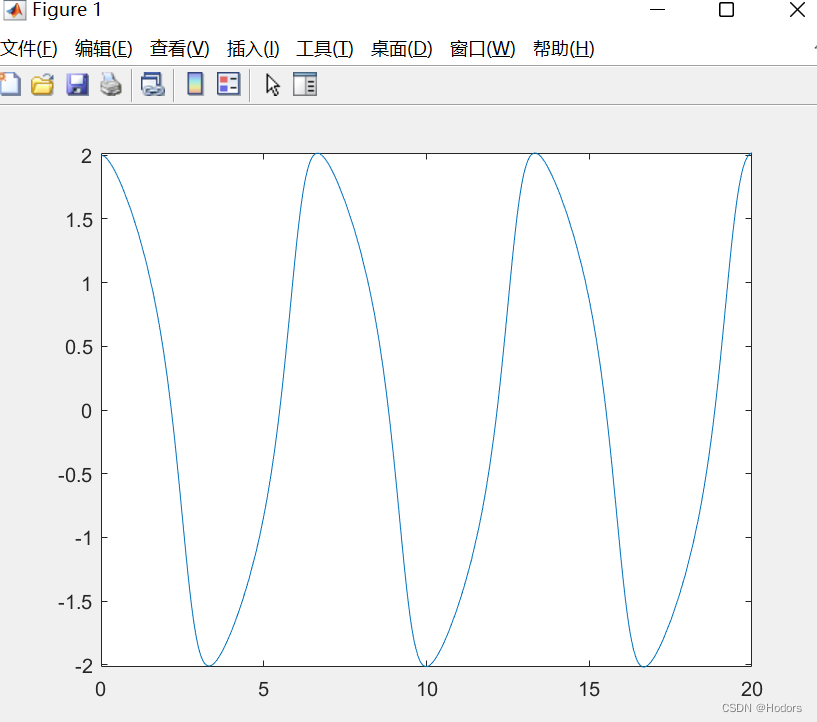
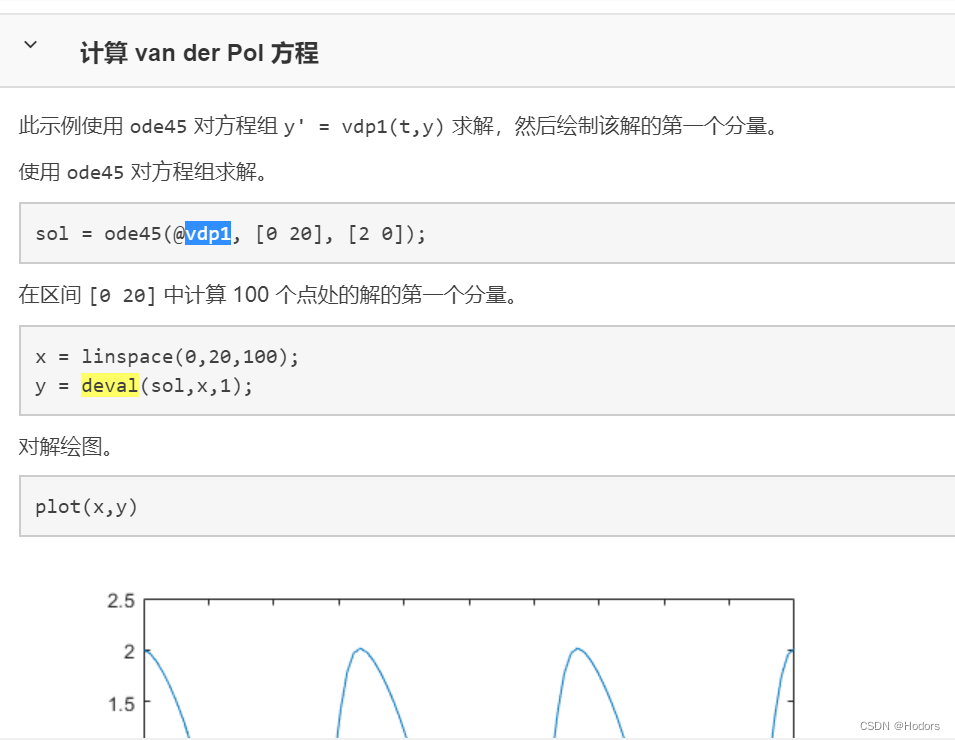
天啊,matlab中,有现成的范德波方程: vdp1
-------------------------
matlab 微分方程
¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥
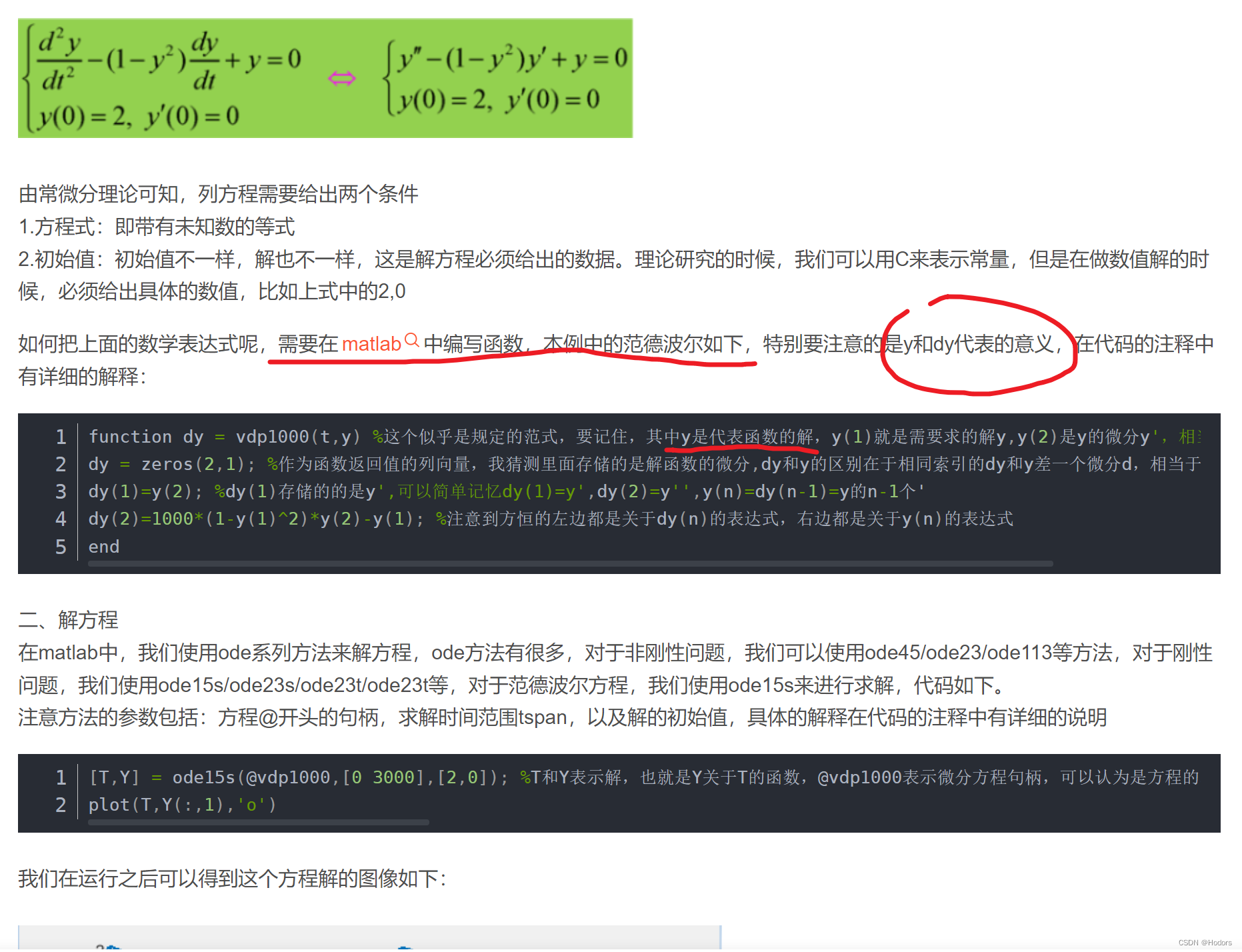
这是定义了一个微分方程,定义的规范是:
%其中y是代表函数的解,
y(1)就是需要求的解y;
y(2)是y的微分y';
相当于y(n)'=y(n+1)
% dy作为函数返回值的列向量,我猜测里面存储的是解函数的微分;
% dy和y的区别在于相同索引的dy和y差一个微分d,
% 相当于dy(1)=y(1)'=y(2)
下边的函数搞成一个文件;
function dy = vdp1000(t, y)
dy = zeros(2,1);
dy(1)=y(2);
dy(2)=1000*(1-y(1)^2)*y(2)-y(1);
end
% dy(1)存储的的是y';
% 可以简单记忆dy(1)=y',dy(2)=y'';
% y(n)=dy(n-1)=y的n-1个'
%注意到方恒的左边都是关于dy(n)的表达式,右边都是关于y(n)的表达式
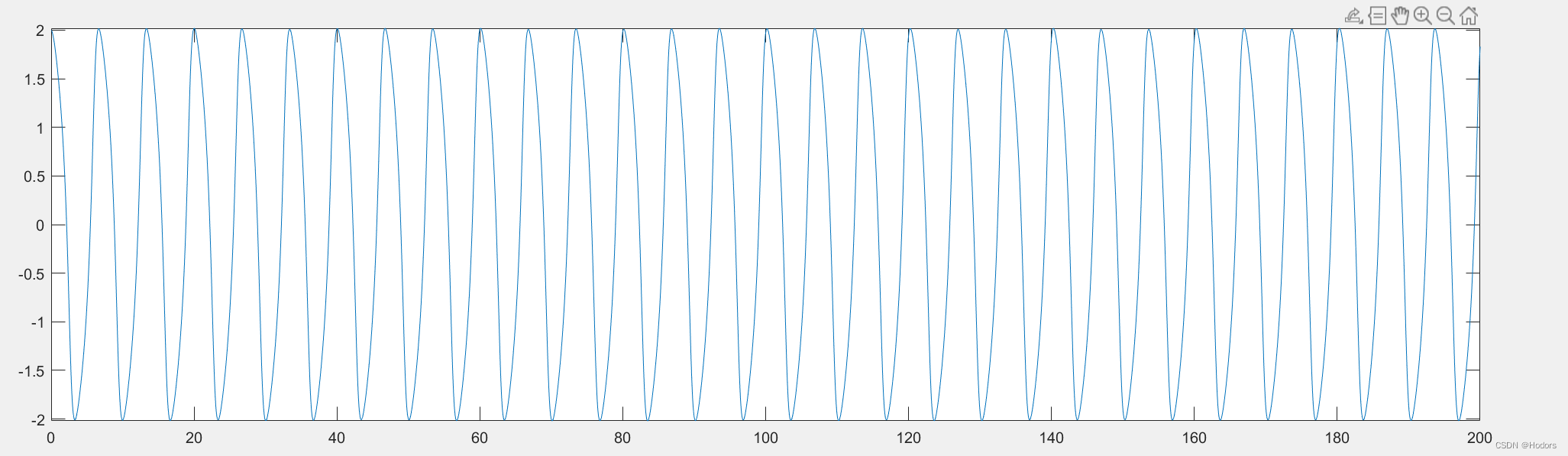
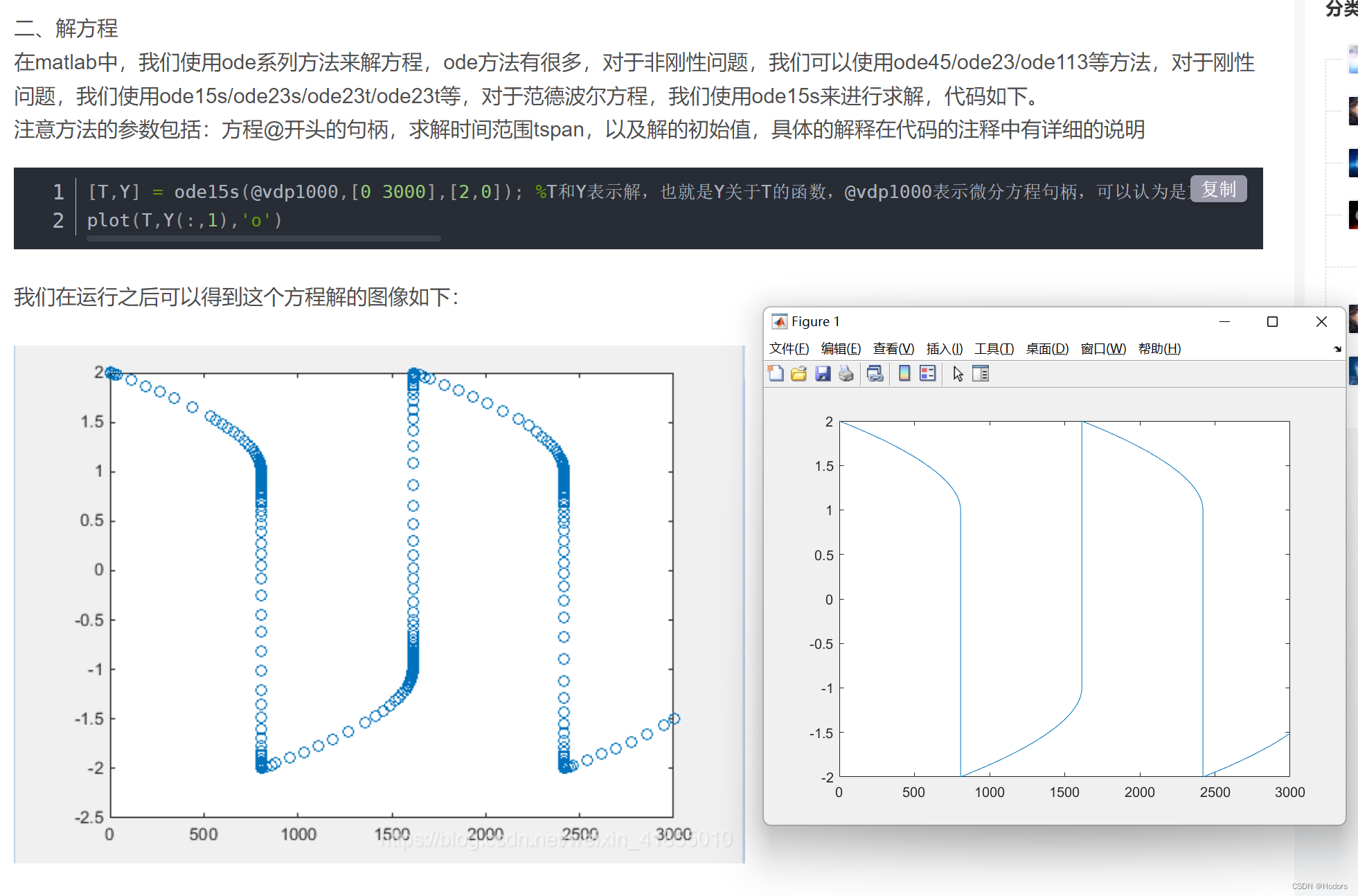
[T,Y] = ode15s(@vdp1000,[0 3000],[2,0]);
%T和Y表示解,也就是Y关于T的函数,@vdp1000表示微分方程句柄,可以认为是方程的名字,比如这里就是范德波尔方程,[0,3000]代表的是时间范围,也就是限定了区间,显然区间越大,计算量越大,所以要想清楚自己要哪一段的数据,给多了也没用。[2,0]表示的是解的初始值,因为初始值不一样,解也不一样,这是解方程必须给出的数据。这里给出了两个初始值,2表示y的初始值,0表示dy的初始值。
plot(T,Y(:,1),'o')
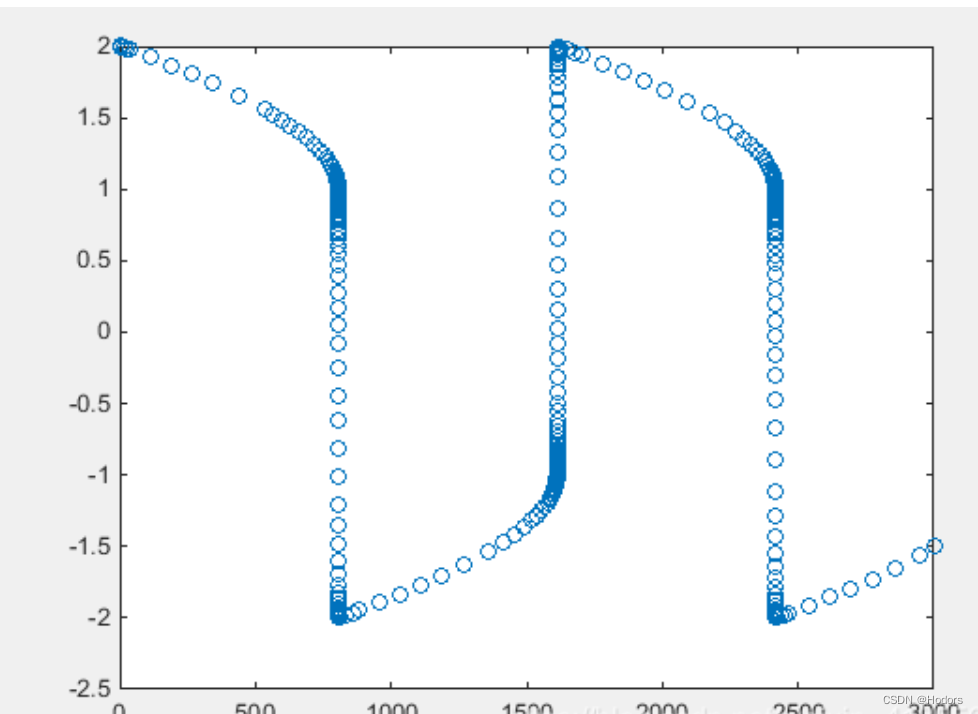
¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥¥
code 如下,结果如右上
% Rewrite the Second-Order ODE as a System of First-Order ODEs
syms y(t);
[V] = odeToVectorField(diff(y, 2) == 1000*(1 - y^2)*diff(y) - y);
% Generate MATLAB Function
M = matlabFunction(V,'vars', {'t','Y'});
% Solve the System of First-Order ODEs
sol = ode45(M,[0 3000],[2 0]);
% Plot the Solution
fplot(@(x)deval(sol,x,1), [0, 3000]);
-------------------
官方文档中这么介绍:
1、求解高阶常微分方程的一种典型方法是将高阶常微分方程转化为一阶微分方程组,然后求解。 该示例使用Symbolic Math Toolbox™将二阶ODE转换为一阶ODE的系统。 然后使用MATLAB求解器ode45对系统进行求解。
2、这个例子向您展示了如何将一个二阶微分方程转换为一个可以使用MATLAB®的数值求解器ode45来求解的微分方程系统。
例子:
Solve a Second-Order Differential Equation Numerically- MATLAB & Simulink- MathWorks 中国

参考:
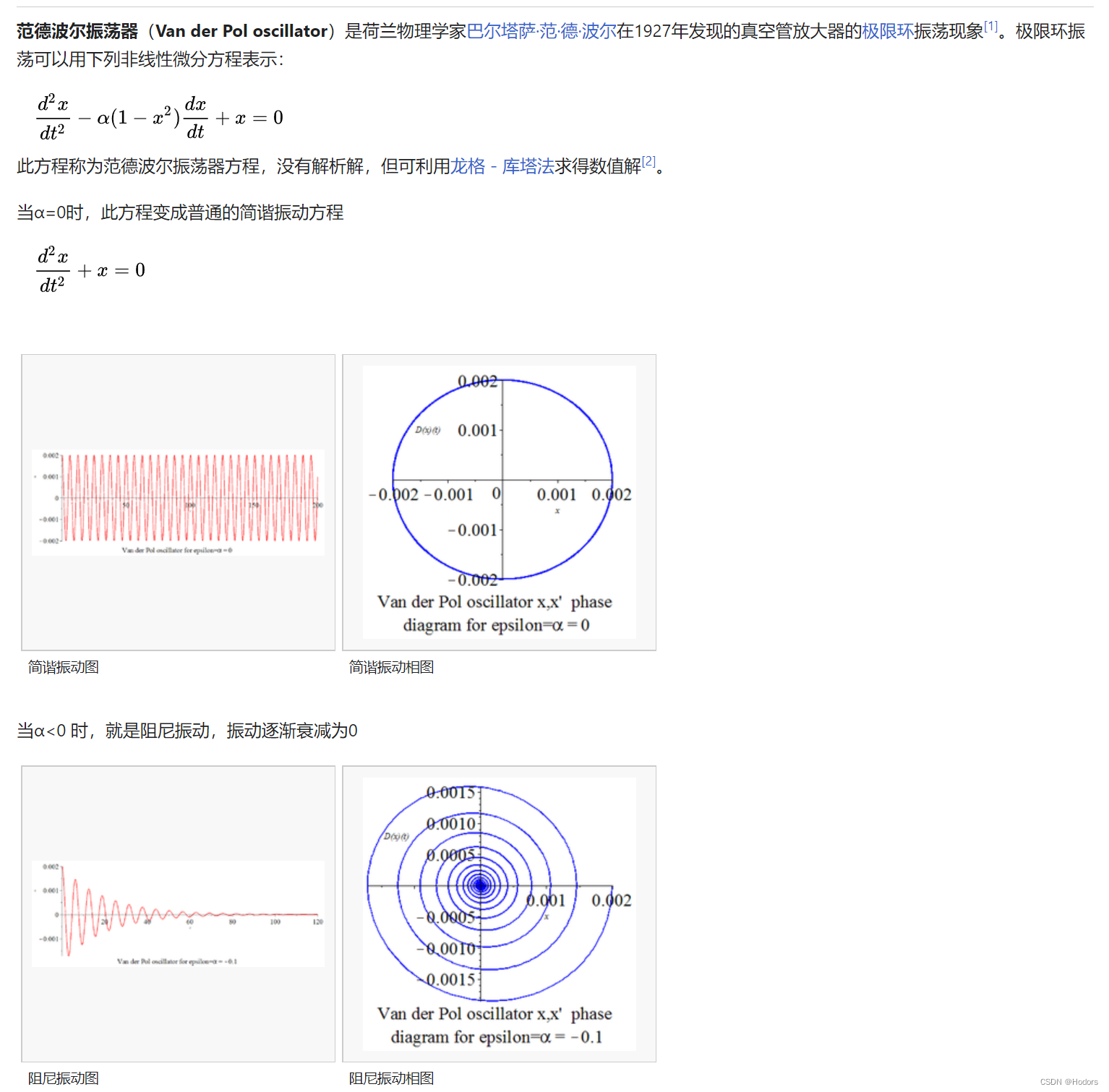
https://zh.m.wikipedia.org/zh-hans/%E8%8C%83%E5%BE%B7%E6%B3%A2%E5%B0%94%E6%8C%AF%E8%8D%A1%E5%99%A8
参考资料:
matlab解微分方程_没想好叫什么名字的博客-CSDN博客_matlab解微分方程
这是最简单的一种求解微分方程的一种方法-符号解法。一般来说,在matlab中解常微分方程有两种方法,一种是符号解法,另一种是数值解法。在本科阶段的微分数学题,基本上可以通过符号解法解决。
ode是最常用的求解微分方程的指令,它采用变步长四、五阶Runge-Kutta-Felhberg法适合高精度问题
matlab中使用ode方法解范德波尔微分方程的数值解_梧桐雪的博客-CSDN博客_范德波尔方程
这个问题的本质是,MATLAB的ode。
在matlab中使用dsolve函数解范德波尔二阶微分方程_梧桐雪的博客-CSDN博客_范德波尔方程matlab编程
有解析解:
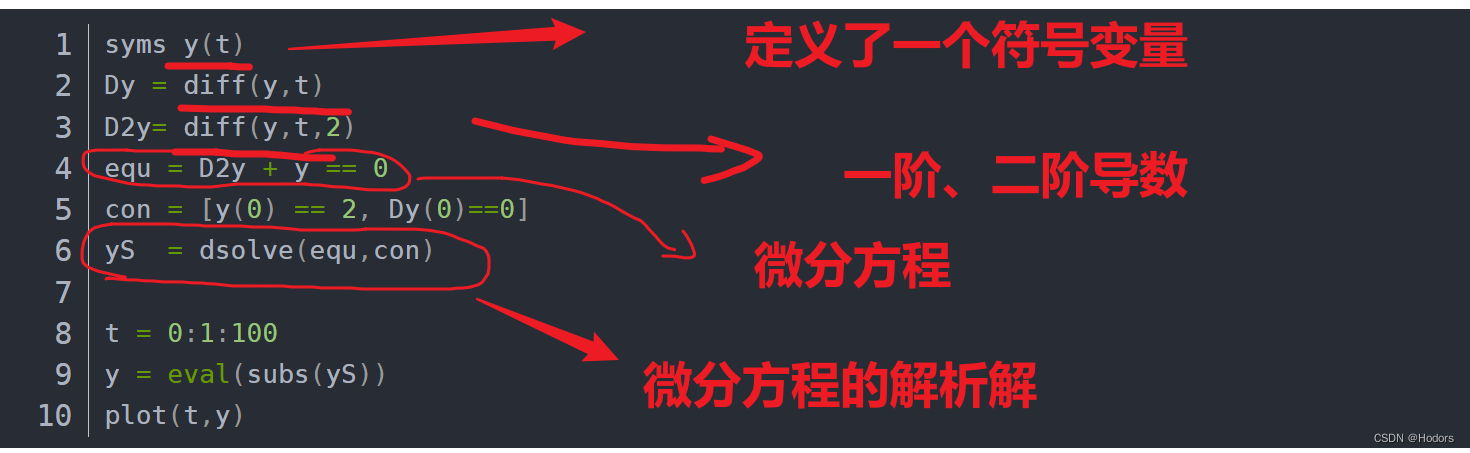
syms y(t)
Dy = diff(y,t)
D2y= diff(y,t,2)
equ = D2y + y == 0
con = [y(0) == 2, Dy(0)==0]
yS = dsolve(equ,con)
t = 0:1:100
y = eval(subs(yS))
plot(t,y)
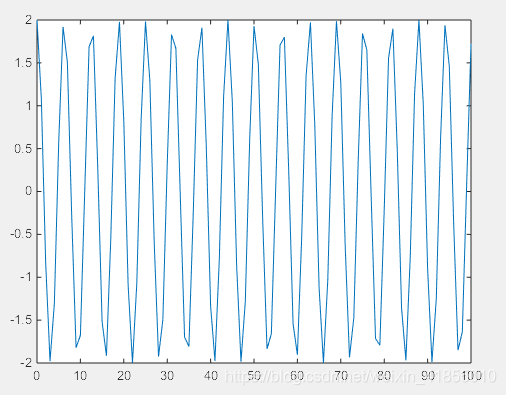
但是这样调整之后,就没有解析解了
clear all;
syms y(t);
u = 0.1;
Dy = diff(y,t);
D2y= diff(y,t,2);
equ = D2y - (1-y*y)*Dy + y == 0;
con = [y(0) == 2, Dy(0)==0];
yS = dsolve(equ,con);

使用数值法进行求解:
Solve a Second-Order Differential Equation Numerically- MATLAB & Simulink- MathWorks 中国
% 如果有解析项,只能通过数值解求得;
% https://ww2.mathworks.cn/help/symbolic/solve-differential-equation-numerically-1.html
% Rewrite the Second-Order ODE as a System of First-Order ODEs
syms y(t);
[V] = odeToVectorField(diff(y, 2) == (1 - y^2)*diff(y) - y);
% Generate MATLAB Function
M = matlabFunction(V,'vars', {'t','Y'});
% Solve the System of First-Order ODEs
sol = ode45(M,[0 20],[2 0]);
% 常见用法:
% [ t , y ] = ode45( odefun , tspan , y0 )
% odefun ,用以表示f(t,y)的函数句柄或inline函数i,t是标量,y是标量或向量;
% tspan 若是二维向量[t0,tf],表示自变量初值t0和终值tf;若是高维向量[t0,t1,...,tn],则表示输出结点列向量;
% y0 初值向量y0;
% t 表示结点列向量(t0,t1,...,tn)^T;
% y 数值解矩阵,每一列对应y的一个分量;
% ode45函数说明:第一个参数是方程的名称,第二个参数是指求解时t的范围,第三组参数是指y中每个元素的初值。
% Plot the Solution
fplot(@(x)deval(sol,x,1), [0, 20]);
参考资料

参考:
在matlab中使用dsolve函数解范德波尔二阶微分方程_梧桐雪的博客-CSDN博客_范德波尔方程matlab编程

matlab中syms是什么意思

matlab中syms与sym有什么区别_爱吃的小花猫_Vigor的博客-CSDN博客_sym和syms的区别

这个解释的也非常清楚:
matlab的符号变量sym,syms_winycg的博客-CSDN博客_matlab sym
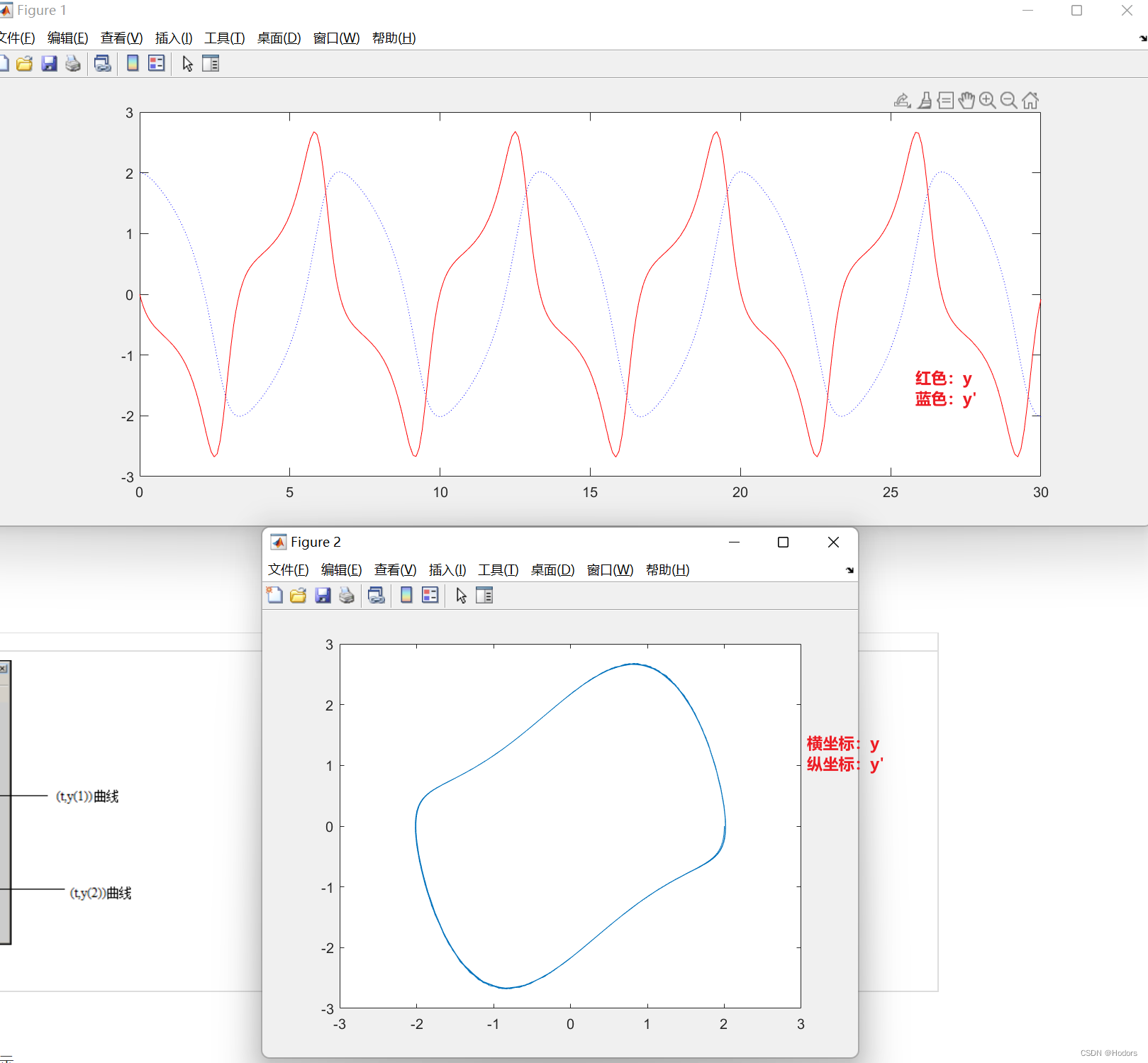
% 另外一种plot方法:
syms y(t);
[V] = odeToVectorField(diff(y, 2) == (1 - y^2)*diff(y) - y);%把高阶变成一阶;
M = matlabFunction(V,'vars', {'t','Y'});
[t, y] = ode45(M,[0 30],[2 0]);
% Plot the Solution
y1=y(:,1); %Y
y2=y(:,2); %Y'
figure(1);
plot(t,y1,':b',t,y2,'-r') %画微分方程解
figure(2);
plot(y1,y2); %画相平面图
% sol = ode45(M,[0 30],[2 0]); sol.x 等价于t, sol.y 等价于y;
[t, y] = ode45(M,[0 30],[2 0]);
-----------------------------------------------------------
2、多个范德波尔振子,耦合成星型网络,
-----------------------------------------------------------



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 三行代码完成国际化适配,妙~啊~
· .NET Core 中如何实现缓存的预热?