如何用龙格库塔 方法求解 范德波振子的运动
如何用龙格库塔 方法求解 范德波振子的运动
坑，没有想好。
这是一个非常好的线索：
Generalized Forced Van Der Pol Oscillator Phase Plot -
function [t,y] = VanderPol(idis, ivel, mu, A, omega)
[t,y] = ode23(@vdp1,[0 20],[2; 0]);
plot(t,y(:,1),'-o',t,y(:,2),'-o')
title('Solution of van der Pol Equation (\mu = 1) with ODE23');
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2')
figure
plot(y(:,1),y(:,2))
title('Phase plane plot')
function dydt = vdp1(t,y)
dydt = [y(2); mu*(1-y(1)^2)*y(2)-y(1)+A*sin(omega*t)];
end
end
在这个代码中，施加了一个外力；
A*sin(omega*t)]
代码这样写，为什们呢？具体有啥规定啊。
---
idis = 2;
ivel = 0;
A = 8;
omega = 4;
mu = 3;
[t,y] = VanderPol(idis, ivel, mu, A, omega);
figure
plot(t,y)
grid
但是这个力不是 岁时间变化的sin函数呢？该怎么办
有想法了：
所有的微分方程组的基本思路：
1、
2、
3、
4、拿 范德波振子举例：
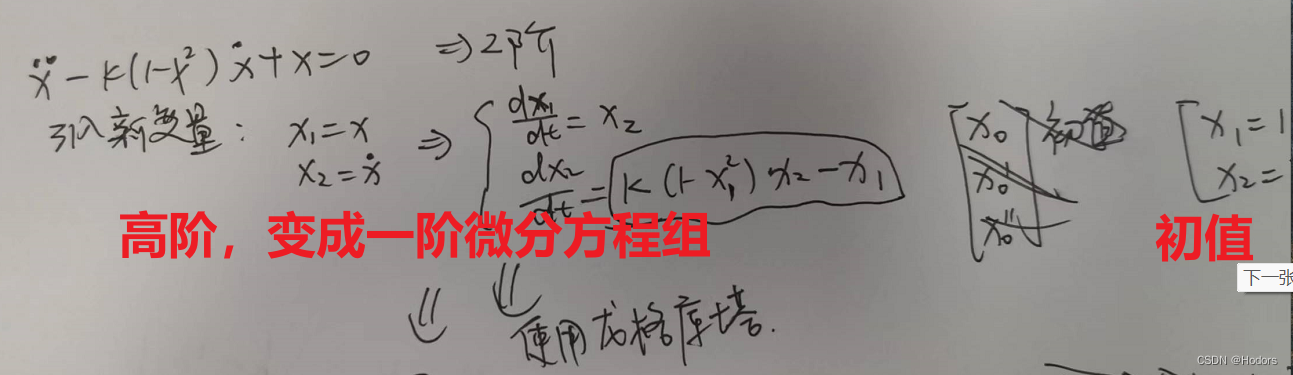
变成了一阶微分方程组之后，
能够非常简单的求得delt x1 和delt x2 如下图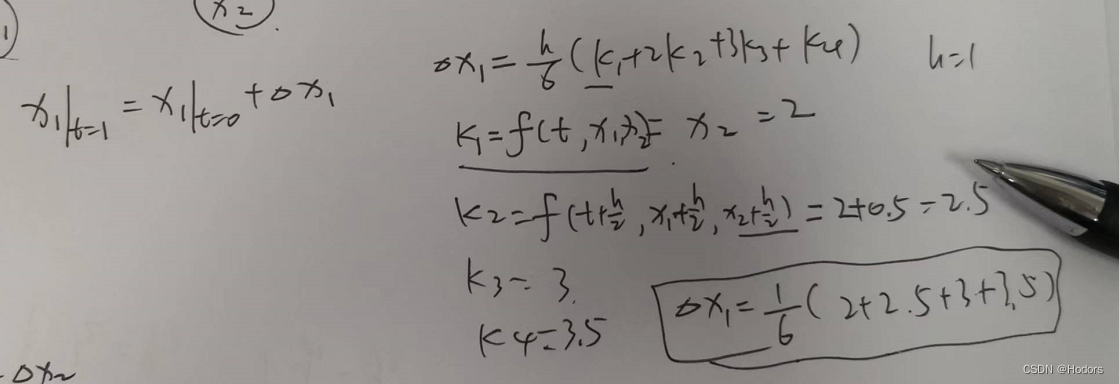
代码如下。
clear all;
x10 = 0.1; %x1代表第一个变量，x2代表第二个变量，后边的0代表的时刻；
x20 = 0.1;
n = 1e4;
x = zeros(n, 2);
x(1, :) = [x10, x20]; %初始条件；
for k=2:n
[dx1, dx2] = dxdt_Vonderpol(x(k-1,1), x(k-1,2));
x(k,1) = x(k-1,1) + dx1;
x(k,2) = x(k-1,2) + dx2;
end
plot(x(:,1));
grid on;
function g=f1(t, x1, x2)
g = x2;
end
function g=f2(t, x1, x2)
k = 1; %范德波振子的衰减系数
e = 0.086; %其他神经元对当前神经元的耦合项；
g = k*(1-x1*x1)*x2 - x1;
end
% ============================================================
% --范德波震荡方程的四阶龙格库塔函数
% ============================================================
function [dx1, dx2] = dxdt_Vonderpol(x1, x2)
h = 1e-2; %步长
K1 = f1(0, x1, x2);
K2 = f1(0, x1 + h*K1/2, x2 + h*K1/2);
K3 = f1(0, x1 + h*K2/2, x2 + h*K2/2);
K4 = f1(0, x1 + h*K3, x2 + h*K3);
L1 = f2(0, x1, x2);
L2 = f2(0, x1 + h*L1/2, x2 + h*L1/2);
L3 = f2(0, x1 + h*L2/2, x2 + h*L2/2);
L4 = f2(0, x1 + h*L3, x2 + h*L3);
dx1 = (K1 + 2*K2 + 2*K3 + K4)*h/6;
dx2 = (L1 + 2*L2 + 2*L3 + L4)*h/6;
end
效果如下：
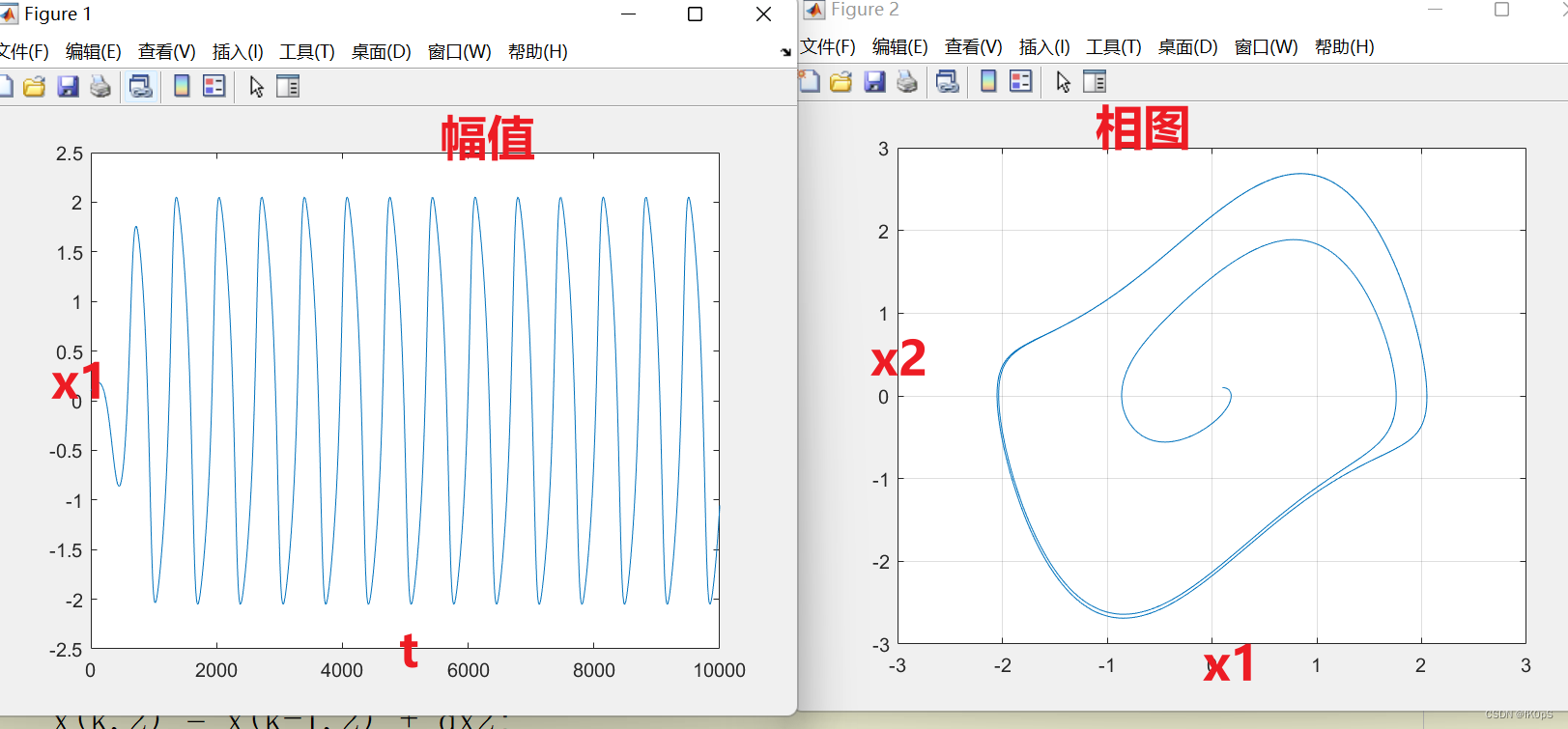
和 微分方程的结果进行对比。
code如下
syms y(t);
[V] = odeToVectorField(diff(y, 2) == (1 - y^2)*diff(y) - y);%把高阶变成一阶；
M = matlabFunction(V,'vars', {'t','Y'});
% sol = ode45(M,[0 30],[2 0]); sol.x 等价于t， sol.y 等价于y；
[t, y] = ode45(M,[0 30],[2 0]);
% Plot the Solution
y1=y(:,1); %Y
y2=y(:,2); %Y'
figure(1);
plot(t,y1,':b',t,y2,'-r') %画微分方程解
figure(2);
plot(y1,y2); %画相平面图
结果：
结论，
（1）两种方法的波形是一致的；
（2）初始条件不会影响收敛的相图；
如果加上其他振子的耦合，是类似的，无非 x.. 的微分方程这一块有一点点不一样。
yes
