MATLAB 构造微分方程的基本知识
0、
关于微分方程你需要了解：含有未知的函数及其某些阶的导数以及其自变量本身的方程称为微分方程。如果未知函数是一元函数，则称为常微分方程。如果未知函数是多元函数，则称为偏微分方程。联系一些未知函数的一组微分方程称为微分方程组。微分方程中出现的未知函数的导数的最高阶称为微分方程的阶。
1、有解析解的方程组；
2、只有数值解的方程组；
3、怎么构造任意的方程组，包括一阶，二阶，三阶。等等。
4、为什么下式这样构造没问题？其合理性是啥？
function dydt = vdp1(t,y)
dydt = [y(2); 3*(1-y(1)^2)*y(2)-y(1)+8*sin(4*t)];
end
5、
6、
7、
8、
在解n个未知函数的方程组时，x0和x均为n维向量，m-文件中的待解方程组应以x的分量形式写成。
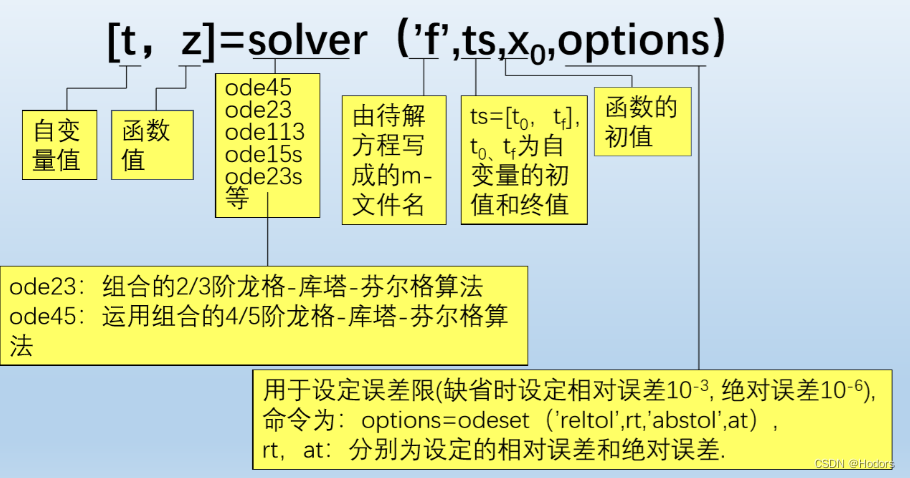
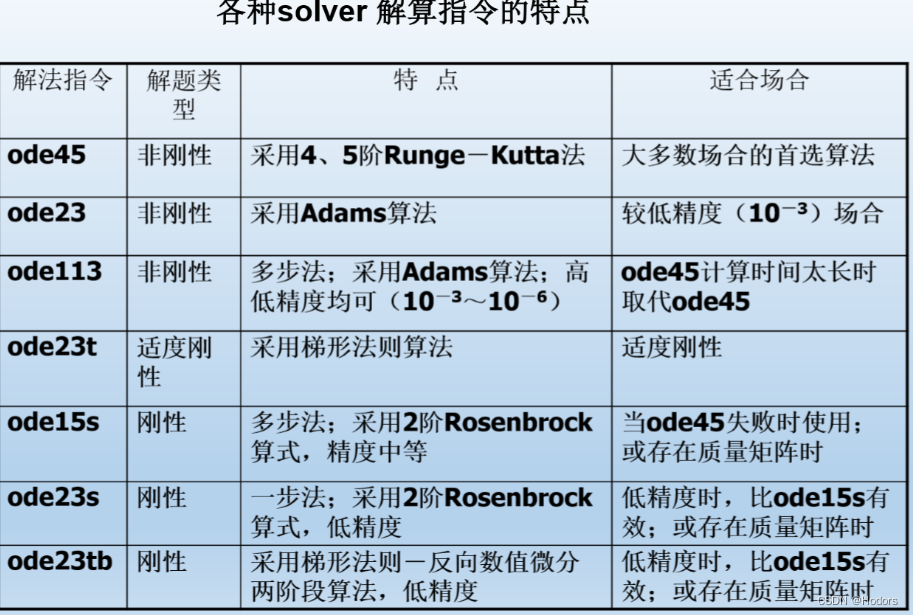
MATLAB提供了7个常微分方程求解器（solver）分别是ode45,ode23,ode113,ode15s,ode23s,ode23t,ode23tb，其中前3个适用于求解非刚性（Nonstiff）问题，后4个适用于刚性问题。
刚性：设有一阶常系数线性微分方程组y’=Ay+f，如果它的Jacobian矩阵的特征值相差十分悬殊；简单点说，就是系统包含多个相互作用但变化速度相差十分悬殊的子过程。
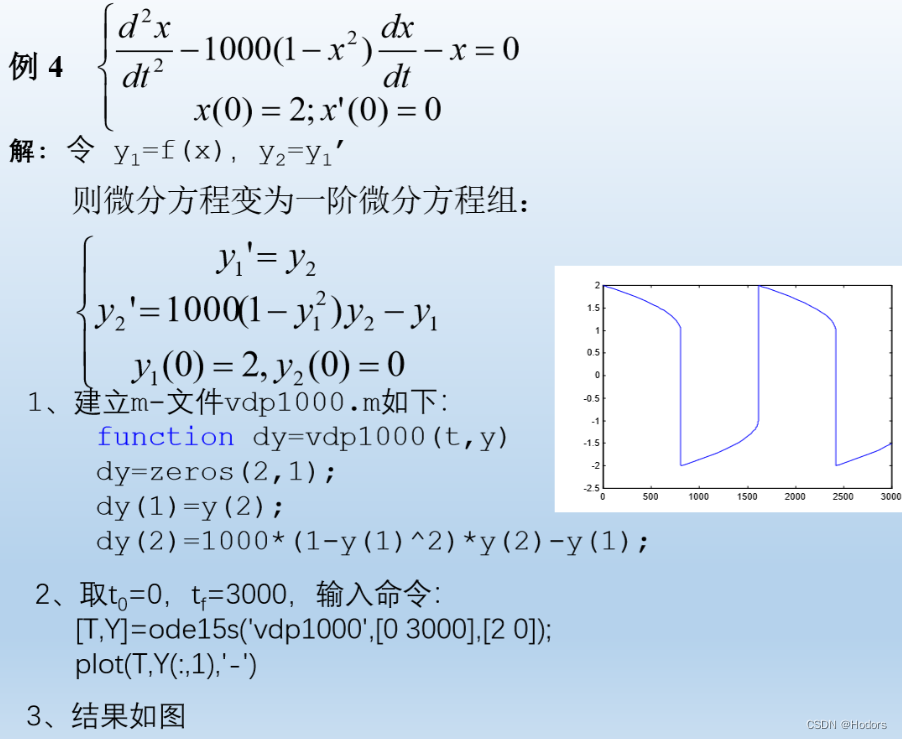
9、为什么要把高阶微分方程组，转化为多个一阶微分方程呢？
主要是为了方便估计斜率， 有了斜率的表达式，就能很方便地得到delt ，从而一步步的进行迭代。
10、数值求解微分方程的关键在于区间上平均斜率的构造。
参考资料：
1、一篇文章带你搞定 MATLAB 求解微分方程（数学建模）_南淮北安的博客-CSDN博客_matlab解一阶微分方程
2、
带你用matlab轻松搞定微分方程 - 云+社区 - 腾讯云
这篇博客抽象的非常好；
3、这个对本质理解的非常深刻
