使用matlab计算 洛伦兹方程 的李雅普诺夫指数

function dX = Lorenz(t,X,params)

a = params(1);
b = params(2);
c = params(3);

x=X(1); 
y=X(2); 
z=X(3);

dX = zeros(3,1);
dX(1)=a*(y-x);
dX(2)=x*(b-z)-y;
dX(3)=x*y-c*z;

end 

%% 计算洛伦兹动力学的李雅普诺夫指数

Z=[];  
a=10; 
c=8/3; 
d0=1e-7; 
bs = linspace(0,300,301);
transient = 50;
for b=bs
    params = [a,b,c];
    lsum=0; 
    x=1;y=1;z=1;   % #初始基准点
    x1=1;y1=1;z1=1+d0;  % #初始偏离点
    for i=1:100  
        [T1,Y1]=ode45(@(t,X) Lorenz(t,X,params),[0 1],[x;y;z]); 
        [T2,Y2]=ode45(@(t,X) Lorenz(t,X,params),[0 1],[x1;y1;z1]); 
        n1=length(Y1);n2=length(Y2);     
        x=Y1(n1,1);y=Y1(n1,2);z=Y1(n1,3);   
        x1=Y2(n2,1);y1=Y2(n2,2);z1=Y2(n2,3);   
        d1=sqrt((x-x1)^2+(y-y1)^2+(z-z1)^2);     
        % #新的偏离点在上一次计算的两轨迹末端的连线上，且距离仍等于d0
        x1=x+(d0/d1)*(x1-x);   
        y1=y+(d0/d1)*(y1-y);    
        z1=z+(d0/d1)*(z1-z); 
        % #舍弃暂态过程的数据，因为初始基准点不一定在吸引子上
        if i> transient
            lsum=lsum+log(d1/d0);  
        end  
    end  
    Z=[Z lsum/(i-transient)]; 
end 

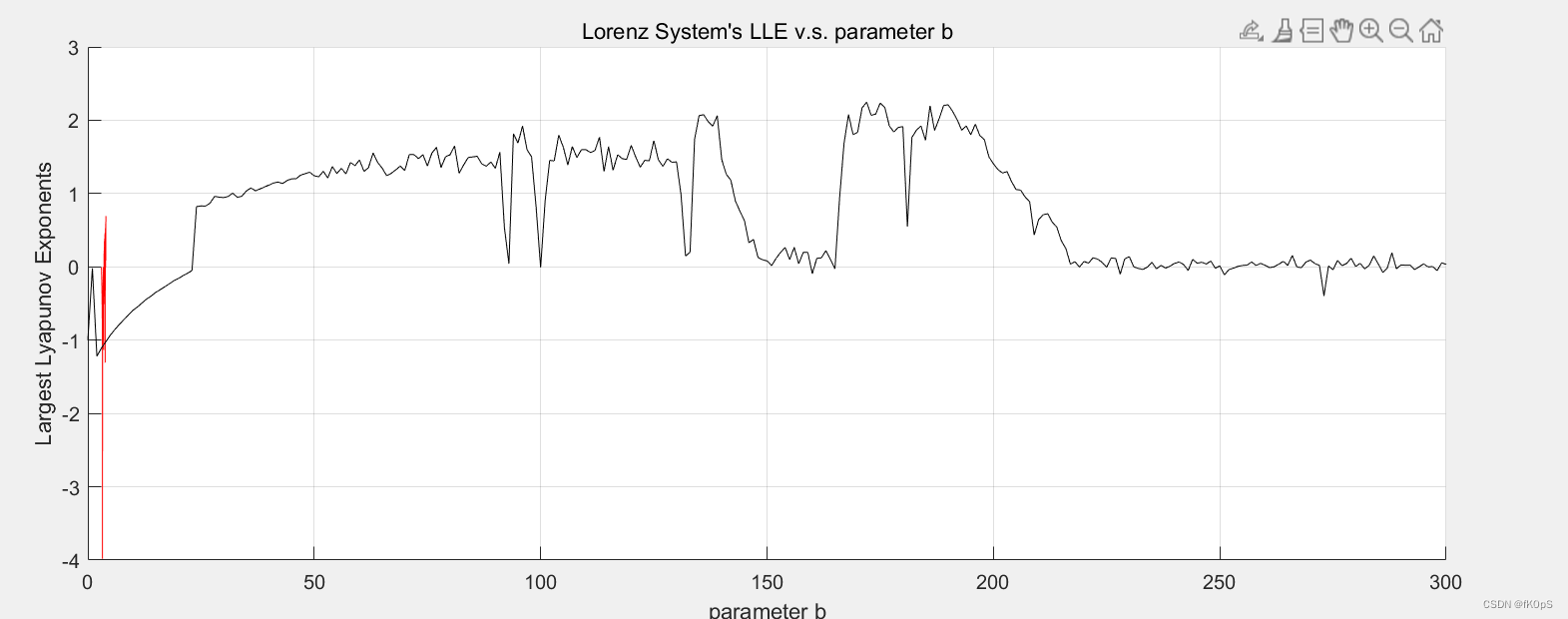
plot(bs,Z,'-k');  
title('Lorenz System''s LLE v.s. parameter b')  
xlabel('parameter b'),ylabel('Largest Lyapunov Exponents'); 
grid on;