范德波振子的李雅普诺夫指数

范德波振子的李雅普诺夫指数

keng

code

%% 计算范德波振子的李雅普诺夫指数
clear all;close all;clc;
Z=zeros(1,100);  %保存结果；
d0=1e-6; %蝴蝶煽动翅膀；
ks = linspace(0,5,100);
transient = 50;

for ii=1:10
    disp(ii);
    lsum=0;
    xxx=1;yyy=1;% #初始基准点
    xxx1=1;yyy1=1+d0;% #初始偏离点
    k = ks(ii);
    
    for i=1:100
        %-----------------------------------------
        %
        syms y(t);
        [V] = odeToVectorField(diff(y, 2) == k*(1 - y^2)*diff(y) - y);%把高阶变成一阶；
        M = matlabFunction(V,'vars', {'t','Y'});
        [t, y] = ode45(M,[0 30],[xxx yyy]);
        n1=length(y);
        xxx=y(n1,1);
        yyy=y(n1,2);  %
        
        syms y(t);
        [V] = odeToVectorField(diff(y, 2) == k*(1 - y^2)*diff(y) - y);%把高阶变成一阶；
        M = matlabFunction(V,'vars', {'t','Y'});
        [t, y] = ode45(M,[0 30],[xxx1 yyy1]);
        n2=length(y);
        xxx1=y(n2,1);
        yyy1=y(n2,2);  %
        %-----------------------------------------
        d1=sqrt((xxx-xxx1)^2+(yyy-yyy1)^2);
        % #新的偏离点在上一次计算的两轨迹末端的连线上，且距离仍等于d0
        xxx1 = xxx + (d0/d1)*(xxx1-xxx);
        yyy1 = yyy + (d0/d1)*(yyy1-yyy);
        
        % #舍弃暂态过程的数据，因为初始基准点不一定在吸引子上
        if i> transient
            lsum=lsum+log(d1/d0);
        end
    end
    Z(ii) = lsum/(i-transient);
end

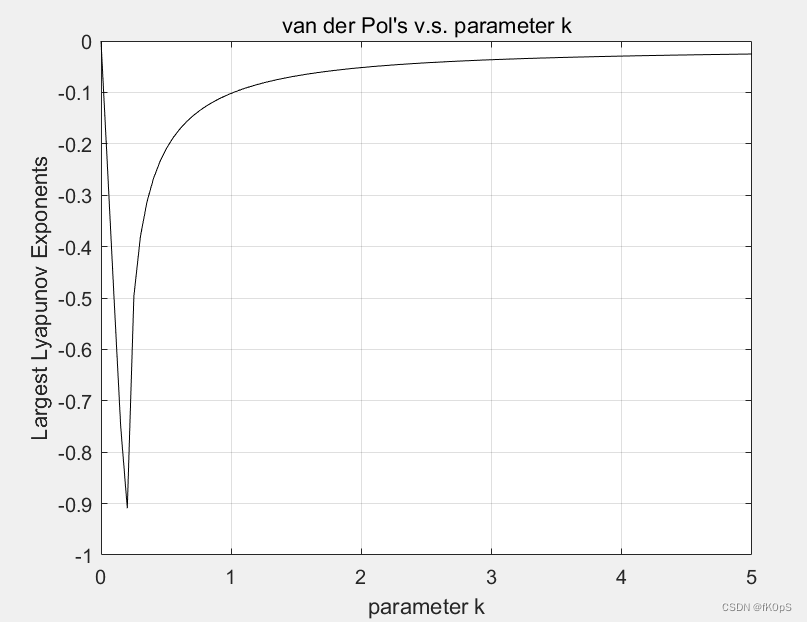
plot(ks,Z,'-k');
title('van der Pol''s v.s. parameter k')  ;
xlabel('parameter k');
ylabel('Largest Lyapunov Exponents');
grid on;

==================================

这是目前为止，最NB的解决方案：  结果如下，根本就混沌不起来啊，感觉

% 范德波振子的方程组；
% 有周期性外力 8*sin(4*t) ；
% y(1) 代表的就是y，振子的幅度；
% y(2) 代表的是y'，振子幅度的一阶导数；

function dydt = vdp1(t,y,params)

    k = params(1);  %外力的幅度和频率也可以是参数；
    dydt = [y(2); k*(1-y(1)^2)*y(2)-y(1)+8*sin(4*t)];

end

-----

%% 计算范德波振子的李雅普诺夫指数  方案1
clear all;close all;clc;
Z=zeros(1,100);  %保存结果；
d0=1e-7; %蝴蝶煽动翅膀；
ks = linspace(0,5,100);
transient = 50;

parfor ii=1:100
    disp(ii);
    lsum=0;
    xxx=1;yyy=1;% #初始基准点
    xxx1=1;yyy1=1+d0;% #初始偏离点
    k = ks(ii);
    params = k;
    
    for i=1:100
        %-----------------------------------------
                
        [T1,Y1]=ode45(@(t,X) vdp1(t,X,params),[0 1],[xxx;yyy]);
        [T2,Y2]=ode45(@(t,X) vdp1(t,X,params),[0 1],[xxx1;yyy1]);
        n1=length(Y1);n2=length(Y2);
        xxx=Y1(n1,1);yyy=Y1(n1,2);
        xxx1=Y2(n2,1);yyy1=Y2(n2,2);
        d1=sqrt((xxx-xxx1)^2+(yyy-yyy1)^2);
        % #新的偏离点在上一次计算的两轨迹末端的连线上，且距离仍等于d0
        xxx1=xxx+(d0/d1)*(xxx1-xxx);
        yyy1=yyy+(d0/d1)*(yyy1-yyy);               
        
        % #舍弃暂态过程的数据，因为初始基准点不一定在吸引子上
        if i> transient
            lsum=lsum+log(d1/d0);
        end
    end
    Z(ii) = lsum/(i-transient);
end

plot(ks,Z,'-k');
title('van der Pol''s v.s. parameter k')  ;
xlabel('parameter k');
ylabel('Largest Lyapunov Exponents');
grid on;
 

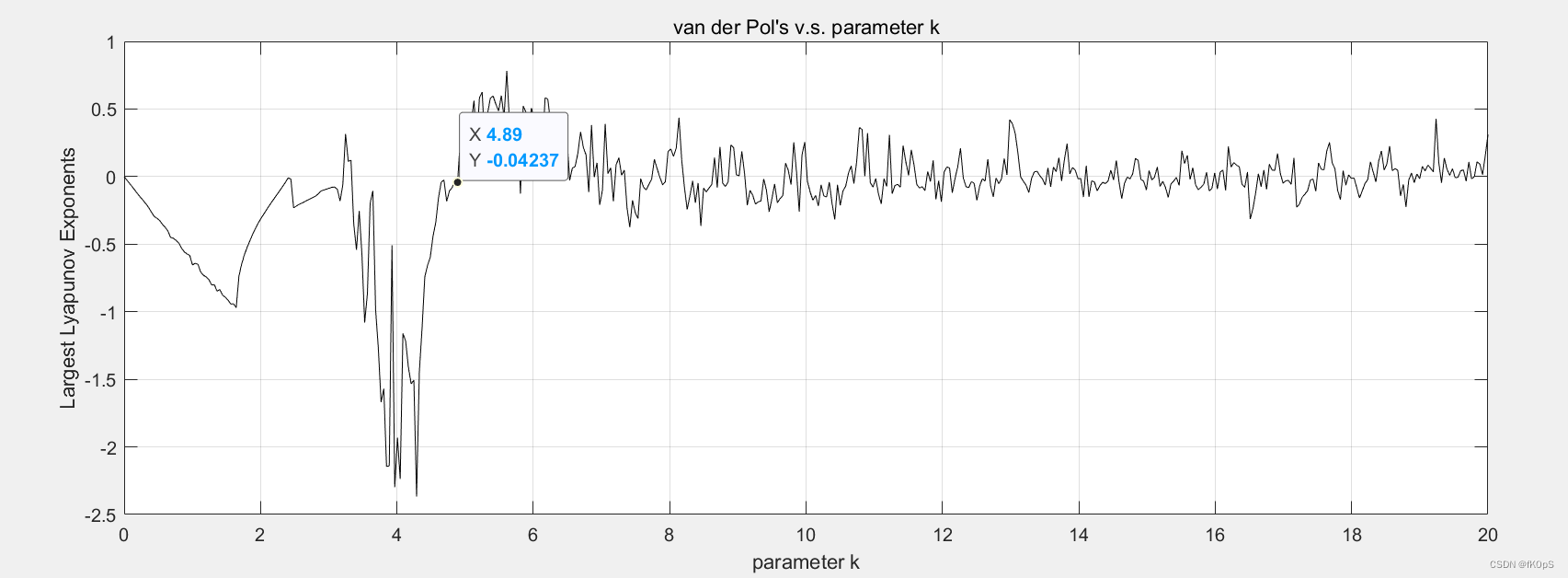
 结论，如果K大于4.8的话，就容易进入混沌状态；