什么是动态规划，什么是背包问题， 计算字符串的编辑距离

什么是动态规划。动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。它比起贪心策略，会分别算出取1、5、11的代价，从而做出一个正确决策，这样就避免掉了“鼠目寸光”！

-----------------------

处理动态规划问题时，需要考虑的points：

1、DP算法的核心是，根据题目，尽可能地缩小解空间：

2、DP的核心思想：尽量缩小可能解空间

3、就是：“未来与过去无关”，这就是无后效性。

4、最优子结构；

-----------------------

1.3万的点赞量，讲解的非常详细： 

什么是动态规划（Dynamic Programming）？动态规划的意义是什么？ - 知乎

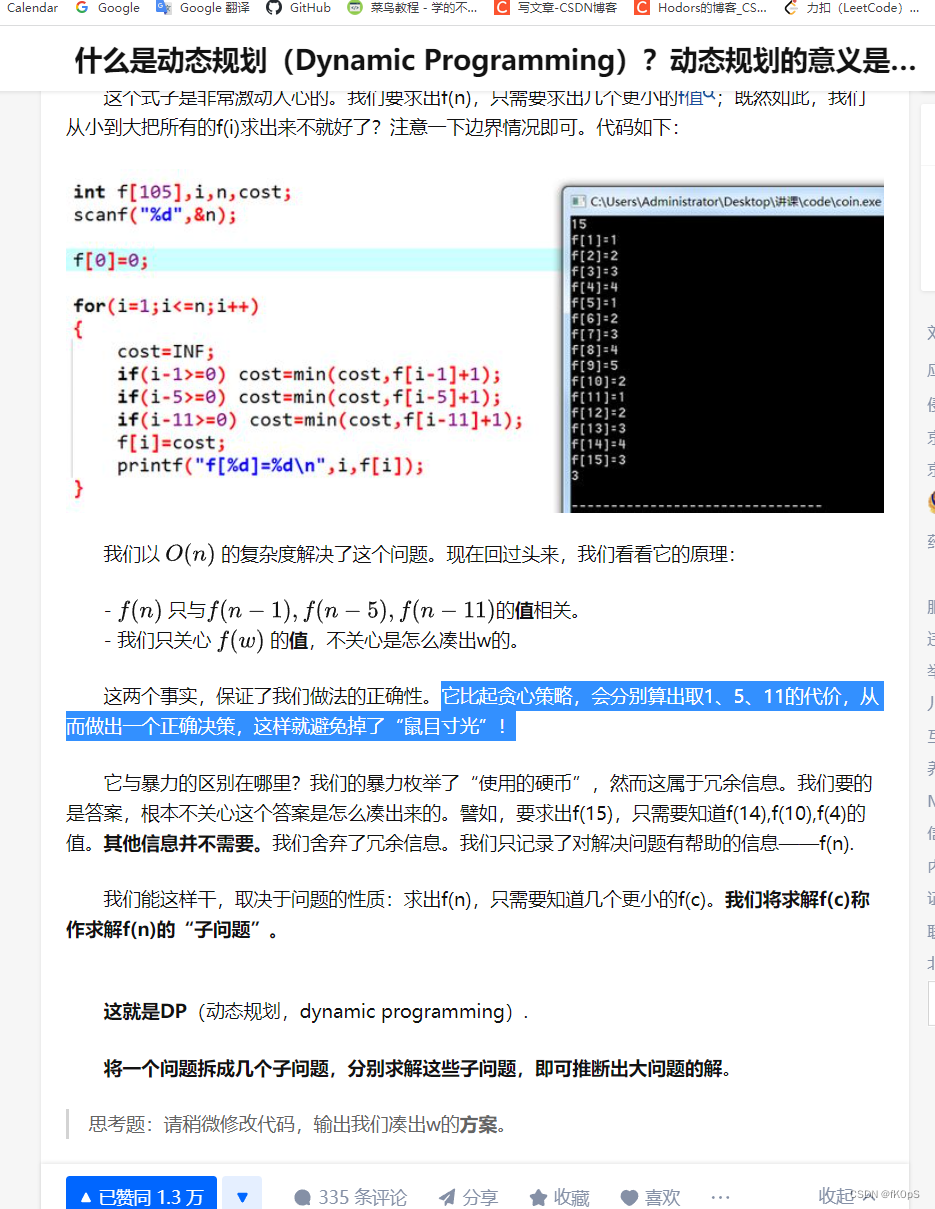
dp动态规划问题，有个重要的特点，

1、就是：“未来与过去无关”，这就是无后效性。

2、最优子结构；

DP算法的核心是，根据题目，尽可能地缩小解空间：

DP的核心思想：尽量缩小可能解空间

背包问题：

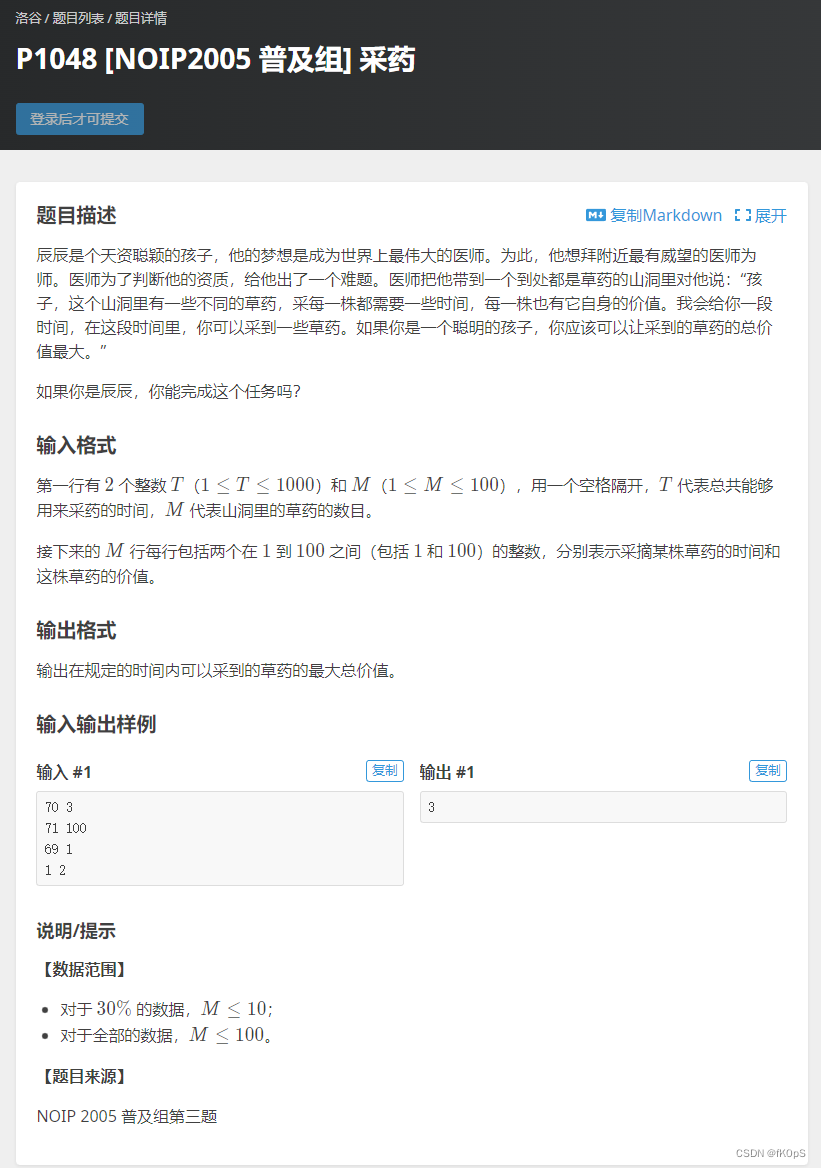
动态规划的典型例题；

----------------------

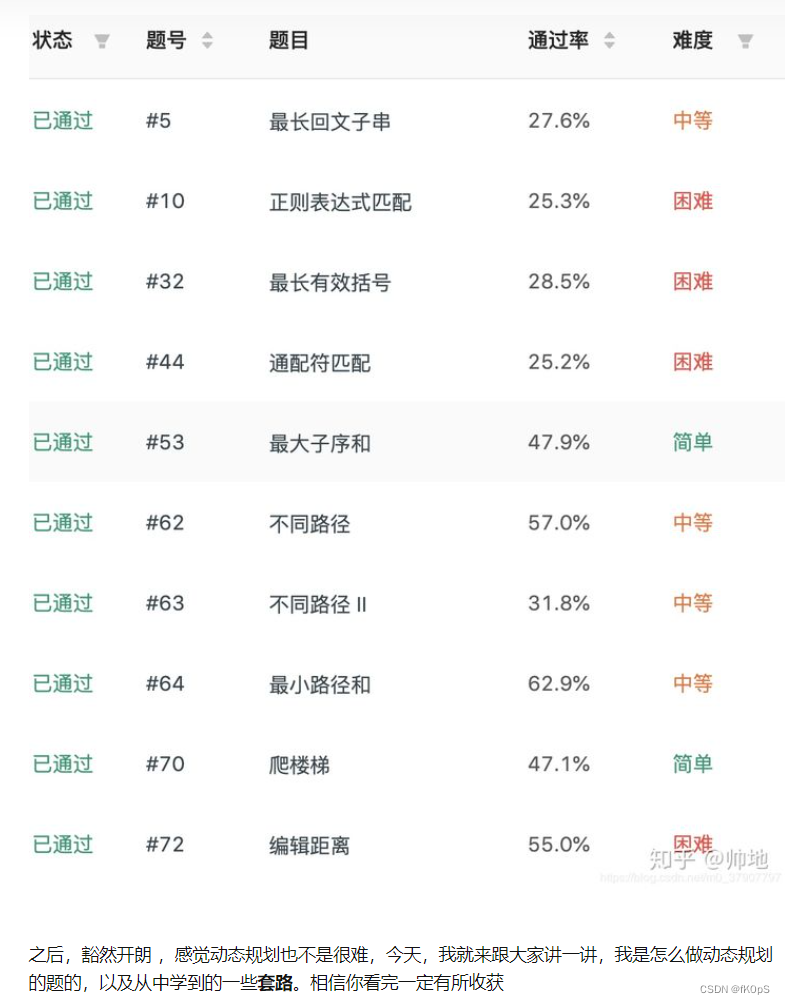
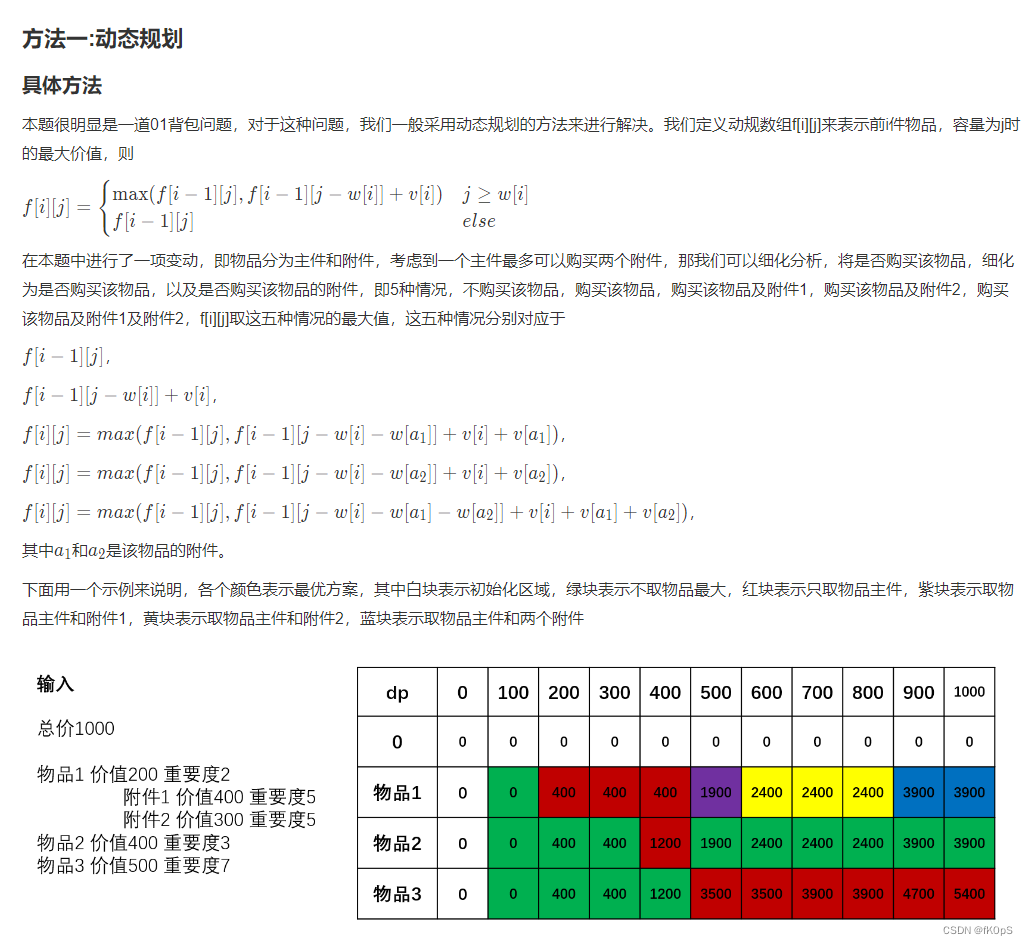
#对于动态规划问题，首先定义个dp函数 

#为什么要倒着来？ 因为是把大问题，化解成小问题；

# 每一种选择，都会对未来有很大的影响，我觉得这是dp问题，最容易让人想不明白的地方；

# 如果发现了一定重复问题，那么一定会有千千万万个重复问题，就像斐波那契数列一样。而重叠子问题是可以通过备忘录解决的

------

递归便于说明问题的解决思路，实际写代码时我们一般采用的还是自底向上的解法，也就是动态规划数组。有了上面的基础，我们很容易能够理解，和公共子串，子序列那些题一样，这道题的数组也一定是一个二维数组

动态规划问题一定要有一个二维数组：

# 一定是一个二维的dp矩阵
m = len(ip1)
n = len(ip2)

dp = [[1 for _ in range(len(ip1)+1)] for _ in range(len(ip2)+1)]
for i in range(1, m+1):
    for j in range(1, n+1):
        if ip1[i-1] == ip2[i-1] :
            dp[i][j] = dp[i-1][j-1]
        else:
            dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1 # 一定要有一次操作