R生存分析AFT
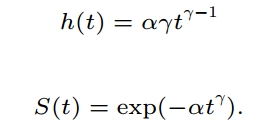
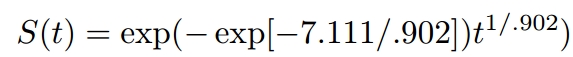
γ = 1/scale =1/0.902
α = exp(−(Intercept)γ)=exp(-(7.111)*γ)
> library(survival)
> myfit=survreg(Surv(futime, fustat)~1 , ovarian, dist="weibull",scale=0)
> summary(myfit)
Call:
survreg(formula = Surv(futime, fustat) ~ 1, data = ovarian, dist = "weibull",
scale = 0)
Value Std. Error z p
(Intercept) 7.111 0.293 24.292 2.36e-130
Log(scale) -0.103 0.254 -0.405 6.86e-01
Scale= 0.902
Weibull distribution
Loglik(model)= -98 Loglik(intercept only)= -98
Number of Newton-Raphson Iterations: 5
n= 26
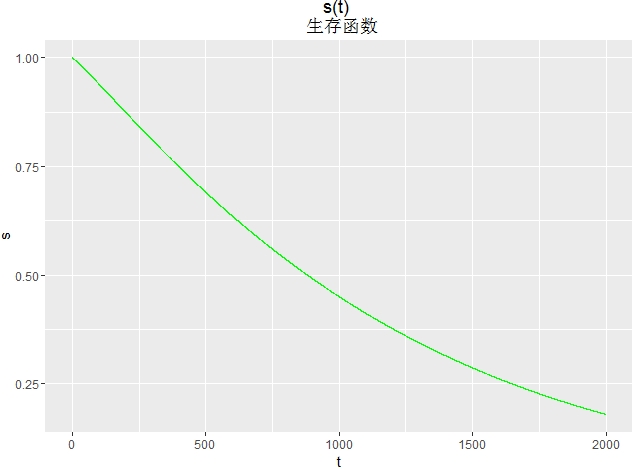
画生存函数图
d<- seq(0, 2000, length.out=10000)
h<-1-pweibull(d,shape=1/0.902,scale=exp(7.111))
df<-data.frame(t=d,s=h)
library(ggplot2)
ggplot(df,aes(x=t,y=s))+
geom_line(colour="green")+
ggtitle("s(t) \n 生存函数")
1. Surv
Description
创建一个生存对象,通常用作模型公式中的响应变量。 参数匹配是此功能的特殊功能,请参阅下面的详细信息。
Surv(time, time2, event,
type=c('right', 'left', 'interval', 'counting', 'interval2', 'mstate'),
origin=0)
is.Surv(x)
Arguments
time
对于右删失数据,这是一个跟踪时间。对于区间数据,第一个参数是区间的开始时间。
event
状态指示,通常,0=活着,1=死亡。其他选择是TRUE/FALSE (TRUE = 死亡) or 1/2 (2=死亡)。对于区间删失数据,状态指示,0=右删失, 1=事件时间, 2=左删失, 3=区间删失.
右删失(Right Censoring):只知道实际寿命大于某数;
左删失(Left Censoring):只知道实际寿命小于某数;
区间删失(Interval Censoring):只知道实际寿命在一个时间区间内。
time2
区间删失区间的结束时间或仅对过程数据进行计数。
type
指定删失类型。 "right", "left", "counting", "interval", "interval2" or "mstate".
如果event变量是一个因子,假定type="mstate"。如果没有指定参数time2,type="right";如果指定参数time2,type="counting"
Surv使用示例
> str(lung) 'data.frame': 228 obs. of 10 variables: $ inst : num 3 3 3 5 1 12 7 11 1 7 ... $ time : num 306 455 1010 210 883 ... $ status : num 2 2 1 2 2 1 2 2 2 2 ... $ age : num 74 68 56 57 60 74 68 71 53 61 ... $ sex : num 1 1 1 1 1 1 2 2 1 1 ... $ ph.ecog : num 1 0 0 1 0 1 2 2 1 2 ... $ ph.karno : num 90 90 90 90 100 50 70 60 70 70 ... $ pat.karno: num 100 90 90 60 90 80 60 80 80 70 ... $ meal.cal : num 1175 1225 NA 1150 NA ... $ wt.loss : num NA 15 15 11 0 0 10 1 16 34 ... > with(lung, Surv(time, status)) [1] 306 455 1010+ 210 883 1022+ 310 361 218 [10] 166 170 654 728 71 567 144 613 707 [19] 61 88 301 81 624 371 394 520 574 [28] 118 390 12 473 26 533 107 53 122 [37] 814 965+ 93 731 460 153 433 145 583 [46] 95 303 519 643 765 735 189 53 246 [55] 689 65 5 132 687 345 444 223 175 [64] 60 163 65 208 821+ 428 230 840+ 305 [73] 11 132 226 426 705 363 11 176 791 [82] 95 196+ 167 806+ 284 641 147 740+ 163 [91] 655 239 88 245 588+ 30 179 310 477 [100] 166 559+ 450 364 107 177 156 529+ 11 [109] 429 351 15 181 283 201 524 13 212 [118] 524 288 363 442 199 550 54 558 207 [127] 92 60 551+ 543+ 293 202 353 511+ 267 [136] 511+ 371 387 457 337 201 404+ 222 62 [145] 458+ 356+ 353 163 31 340 229 444+ 315+ [154] 182 156 329 364+ 291 179 376+ 384+ 268 [163] 292+ 142 413+ 266+ 194 320 181 285 301+ [172] 348 197 382+ 303+ 296+ 180 186 145 269+ [181] 300+ 284+ 350 272+ 292+ 332+ 285 259+ 110 [190] 286 270 81 131 225+ 269 225+ 243+ 279+ [199] 276+ 135 79 59 240+ 202+ 235+ 105 224+ [208] 239 237+ 173+ 252+ 221+ 185+ 92+ 13 222+ [217] 192+ 183 211+ 175+ 197+ 203+ 116 188+ 191+ [226] 105+ 174+ 177+ > str(heart) 'data.frame': 172 obs. of 8 variables: $ start : num 0 0 0 1 0 36 0 0 0 51 ... $ stop : num 50 6 1 16 36 39 18 3 51 675 ... $ event : num 1 1 0 1 0 1 1 1 0 1 ... $ age : num -17.16 3.84 6.3 6.3 -7.74 ... $ year : num 0.123 0.255 0.266 0.266 0.49 ... $ surgery : num 0 0 0 0 0 0 0 0 0 0 ... $ transplant: Factor w/ 2 levels "0","1": 1 1 1 2 1 2 1 1 1 2 ... $ id : num 1 2 3 3 4 4 5 6 7 7 ... > Surv(heart$start, heart$stop, heart$event) [1] ( 0.0, 50.0] ( 0.0, 6.0] ( 0.0, 1.0+] [4] ( 1.0, 16.0] ( 0.0, 36.0+] ( 36.0, 39.0] [7] ( 0.0, 18.0] ( 0.0, 3.0] ( 0.0, 51.0+] [10] ( 51.0, 675.0] ( 0.0, 40.0] ( 0.0, 85.0] [13] ( 0.0, 12.0+] ( 12.0, 58.0] ( 0.0, 26.0+] [16] ( 26.0, 153.0] ( 0.0, 8.0] ( 0.0, 17.0+] [19] ( 17.0, 81.0] ( 0.0, 37.0+] ( 37.0,1387.0] [22] ( 0.0, 1.0] ( 0.0, 28.0+] ( 28.0, 308.0] [25] ( 0.0, 36.0] ( 0.0, 20.0+] ( 20.0, 43.0] [28] ( 0.0, 37.0] ( 0.0, 18.0+] ( 18.0, 28.0] [31] ( 0.0, 8.0+] ( 8.0,1032.0] ( 0.0, 12.0+] [34] ( 12.0, 51.0] ( 0.0, 3.0+] ( 3.0, 733.0] [37] ( 0.0, 83.0+] ( 83.0, 219.0] ( 0.0, 25.0+] [40] ( 25.0,1800.0+] ( 0.0,1401.0+] ( 0.0, 263.0] [43] ( 0.0, 71.0+] ( 71.0, 72.0] ( 0.0, 35.0] [46] ( 0.0, 16.0+] ( 16.0, 852.0] ( 0.0, 16.0] [49] ( 0.0, 17.0+] ( 17.0, 77.0] ( 0.0, 51.0+] [52] ( 51.0,1587.0+] ( 0.0, 23.0+] ( 23.0,1572.0+] [55] ( 0.0, 12.0] ( 0.0, 46.0+] ( 46.0, 100.0] [58] ( 0.0, 19.0+] ( 19.0, 66.0] ( 0.0, 4.5+] [61] ( 4.5, 5.0] ( 0.0, 2.0+] ( 2.0, 53.0] [64] ( 0.0, 41.0+] ( 41.0,1408.0+] ( 0.0, 58.0+] [67] ( 58.0,1322.0+] ( 0.0, 3.0] ( 0.0, 2.0] [70] ( 0.0, 40.0] ( 0.0, 1.0+] ( 1.0, 45.0] [73] ( 0.0, 2.0+] ( 2.0, 996.0] ( 0.0, 21.0+] [76] ( 21.0, 72.0] ( 0.0, 9.0] ( 0.0, 36.0+] [79] ( 36.0,1142.0+] ( 0.0, 83.0+] ( 83.0, 980.0] [82] ( 0.0, 32.0+] ( 32.0, 285.0] ( 0.0, 102.0] [85] ( 0.0, 41.0+] ( 41.0, 188.0] ( 0.0, 3.0] [88] ( 0.0, 10.0+] ( 10.0, 61.0] ( 0.0, 67.0+] [91] ( 67.0, 942.0+] ( 0.0, 149.0] ( 0.0, 21.0+] [94] ( 21.0, 343.0] ( 0.0, 78.0+] ( 78.0, 916.0+] [97] ( 0.0, 3.0+] ( 3.0, 68.0] ( 0.0, 2.0] [100] ( 0.0, 69.0] ( 0.0, 27.0+] ( 27.0, 842.0+] [103] ( 0.0, 33.0+] ( 33.0, 584.0] ( 0.0, 12.0+] [106] ( 12.0, 78.0] ( 0.0, 32.0] ( 0.0, 57.0+] [109] ( 57.0, 285.0] ( 0.0, 3.0+] ( 3.0, 68.0] [112] ( 0.0, 10.0+] ( 10.0, 670.0+] ( 0.0, 5.0+] [115] ( 5.0, 30.0] ( 0.0, 31.0+] ( 31.0, 620.0+] [118] ( 0.0, 4.0+] ( 4.0, 596.0+] ( 0.0, 27.0+] [121] ( 27.0, 90.0] ( 0.0, 5.0+] ( 5.0, 17.0] [124] ( 0.0, 2.0] ( 0.0, 46.0+] ( 46.0, 545.0+] [127] ( 0.0, 21.0] ( 0.0, 210.0+] (210.0, 515.0+] [130] ( 0.0, 67.0+] ( 67.0, 96.0] ( 0.0, 26.0+] [133] ( 26.0, 482.0+] ( 0.0, 6.0+] ( 6.0, 445.0+] [136] ( 0.0, 428.0+] ( 0.0, 32.0+] ( 32.0, 80.0] [139] ( 0.0, 37.0+] ( 37.0, 334.0] ( 0.0, 5.0] [142] ( 0.0, 8.0+] ( 8.0, 397.0+] ( 0.0, 60.0+] [145] ( 60.0, 110.0] ( 0.0, 31.0+] ( 31.0, 370.0+] [148] ( 0.0, 139.0+] (139.0, 207.0] ( 0.0, 160.0+] [151] (160.0, 186.0] ( 0.0, 340.0] ( 0.0, 310.0+] [154] (310.0, 340.0+] ( 0.0, 28.0+] ( 28.0, 265.0+] [157] ( 0.0, 4.0+] ( 4.0, 165.0] ( 0.0, 2.0+] [160] ( 2.0, 16.0] ( 0.0, 13.0+] ( 13.0, 180.0+] [163] ( 0.0, 21.0+] ( 21.0, 131.0+] ( 0.0, 96.0+] [166] ( 96.0, 109.0+] ( 0.0, 21.0] ( 0.0, 38.0+] [169] ( 38.0, 39.0+] ( 0.0, 31.0+] ( 0.0, 11.0+] [172] ( 0.0, 6.0]
2.survreg
拟合参数生存回归模型。 这些是用于时间变量的任意变换的位置尺度模型; 最常见的情况使用对数变换,建立加速失效时间模型。
survreg(formula, data, weights, subset,
na.action, dist="weibull", init=NULL, scale=0,
control,parms=NULL,model=FALSE, x=FALSE,
y=TRUE, robust=FALSE, score=FALSE, ...)
dist
y变量的假设分布。"weibull", "exponential", "gaussian", "logistic","lognormal" and "loglogistic"。
scale
可选的固定值。如果设置<=0,scale将被估计
# survreg's scale = 1/(rweibull shape) # survreg's intercept = log(rweibull scale) # survreg结果中输出的scale与“rweibull scale”不同
control
控制值列表,参考survreg.control()
survreg.control
survreg.control(maxiter=30, rel.tolerance=1e-09,
toler.chol=1e-10, iter.max, debug=0, outer.max=10)
maxiter
最大迭代次数
rel.tolerance
“相对容忍度”来声明收敛
toler.chol
Tolerance to declare Cholesky decomposition singular
iter.max
与maxiter相同
debug
打印调试信息
outer.max
用于选择惩罚参数的外部迭代的最大数目
convergence tolerance
/x(k+1)/=/x(k)/*Tr+Ta
其中:
k 迭代次数;
x(k+1) x的k次迭代计算值;
x(k) x的k次迭代初始值;
Tr 相对误差
Ta绝对误差
// 表示绝对值
因此,从上述公式我们可以得到一个重要结论:设定计算迭代误差的时候,要全面权衡物理量的绝对值大小,同时要衡量收敛迭代值的相对误差,这样才能正确满意的设定自己需要的计算误差!
不能简单的以为绝对误差和相对误差越小越好,也要杜绝tolerance设定时的随意性(按照公式进行合理的设定是一个优秀的过程工程师的基本素质)
survreg使用示例
> library(survival)
> str(ovarian)
'data.frame': 26 obs. of 6 variables:
$ futime : num 59 115 156 421 431 448 464 475 477 563 ...
$ fustat : num 1 1 1 0 1 0 1 1 0 1 ...
$ age : num 72.3 74.5 66.5 53.4 50.3 ...
$ resid.ds: num 2 2 2 2 2 1 2 2 2 1 ...
$ rx : num 1 1 1 2 1 1 2 2 1 2 ...
$ ecog.ps : num 1 1 2 1 1 2 2 2 1 2 ...
> # 拟合指数模型,以下2个模型是一样的
> survreg(Surv(futime, fustat) ~ ecog.ps + rx, ovarian, dist='weibull',
+ scale=1)
Call:
survreg(formula = Surv(futime, fustat) ~ ecog.ps + rx, data = ovarian,
dist = "weibull", scale = 1)
Coefficients:
(Intercept) ecog.ps rx
6.9618376 -0.4331347 0.5815027
Scale fixed at 1 # 注意这里
Loglik(model)= -97.2 Loglik(intercept only)= -98
Chisq= 1.67 on 2 degrees of freedom, p= 0.43
n= 26
> survreg(Surv(futime, fustat) ~ ecog.ps + rx, ovarian,
+ dist="exponential")
Call:
survreg(formula = Surv(futime, fustat) ~ ecog.ps + rx, data = ovarian,
dist = "exponential")
Coefficients:
(Intercept) ecog.ps rx
6.9618376 -0.4331347 0.5815027
Scale fixed at 1 # 注意这里
Loglik(model)= -97.2 Loglik(intercept only)= -98
Chisq= 1.67 on 2 degrees of freedom, p= 0.43
n= 26
> ##########################################
>
> str(lung)
'data.frame': 228 obs. of 10 variables:
$ inst : num 3 3 3 5 1 12 7 11 1 7 ...
$ time : num 306 455 1010 210 883 ...
$ status : num 2 2 1 2 2 1 2 2 2 2 ...
$ age : num 74 68 56 57 60 74 68 71 53 61 ...
$ sex : num 1 1 1 1 1 1 2 2 1 1 ...
$ ph.ecog : num 1 0 0 1 0 1 2 2 1 2 ...
$ ph.karno : num 90 90 90 90 100 50 70 60 70 70 ...
$ pat.karno: num 100 90 90 60 90 80 60 80 80 70 ...
$ meal.cal : num 1175 1225 NA 1150 NA ...
$ wt.loss : num NA 15 15 11 0 0 10 1 16 34 ...
> # weibull分布,如果设置scale<=0,模型将使用最大似然估计,估计最优的scale
> myfit<-survreg(Surv(time, status) ~ ph.ecog + age + sex, data=lung,dist = "weibull")
> myfit
Call:
survreg(formula = Surv(time, status) ~ ph.ecog + age + sex, data = lung,
dist = "weibull")
Coefficients:
(Intercept) ph.ecog age sex
6.273435252 -0.339638098 -0.007475439 0.401090541
Scale= 0.731109
Loglik(model)= -1132.4 Loglik(intercept only)= -1147.4
Chisq= 29.98 on 3 degrees of freedom, p= 1.4e-06
n=227 (1 observation deleted due to missingness)
> summary(myfit)
Call:
survreg(formula = Surv(time, status) ~ ph.ecog + age + sex, data = lung,
dist = "weibull")
Value Std. Error z p
(Intercept) 6.27344 0.45358 13.83 1.66e-43
ph.ecog -0.33964 0.08348 -4.07 4.73e-05
age -0.00748 0.00676 -1.11 2.69e-01
sex 0.40109 0.12373 3.24 1.19e-03
Log(scale) -0.31319 0.06135 -5.11 3.30e-07
Scale= 0.731
Weibull distribution
Loglik(model)= -1132.4 Loglik(intercept only)= -1147.4
Chisq= 29.98 on 3 degrees of freedom, p= 1.4e-06
Number of Newton-Raphson Iterations: 5
n=227 (1 observation deleted due to missingness)
# survreg's scale = 1/(rweibull shape)
# survreg's intercept = log(rweibull scale)
# survreg结果中输出的scale与“rweibull scale”不同
##############################################
> # weibull分布,以sex对数据分组,产生2个不同的scale
> myfit1<-survreg(Surv(time, status) ~ ph.ecog + age + strata(sex), data=lung,dist = "weibull")
> summary(myfit1)
Call:
survreg(formula = Surv(time, status) ~ ph.ecog + age + strata(sex),
data = lung, dist = "weibull")
Value Std. Error z p
(Intercept) 6.73235 0.42396 15.880 8.75e-57
ph.ecog -0.32443 0.08649 -3.751 1.76e-04
age -0.00581 0.00693 -0.838 4.02e-01
sex=1 -0.24408 0.07920 -3.082 2.06e-03
sex=2 -0.42345 0.10669 -3.969 7.22e-05
Scale:
sex=1 sex=2
0.783 0.655
Weibull distribution
Loglik(model)= -1137.3 Loglik(intercept only)= -1146.2
Chisq= 17.8 on 2 degrees of freedom, p= 0.00014
Number of Newton-Raphson Iterations: 5
n=227 (1 observation deleted due to missingness)
################################################
# 具有高斯误差的线性回归,以及左删失数据
> survreg(Surv(durable, durable>0, type='left') ~ age + quant,
+ data=tobin, dist='gaussian', scale = 0)
Call:
survreg(formula = Surv(durable, durable > 0, type = "left") ~
age + quant, data = tobin, dist = "gaussian", scale = 0)
Coefficients:
(Intercept) age quant
15.14486636 -0.12905928 -0.04554166
Scale= 5.57254
Loglik(model)= -28.9 Loglik(intercept only)= -29.5
Chisq= 1.1 on 2 degrees of freedom, p= 0.58
n= 20
3.survdiff
测试在两条或更多条生存曲线之间是否存在差异
survdiff(formula, data, subset, na.action, rho=0)
rho = 0 表示log-rank or Mantel-Haenszel检验;
rho = 1 表示Wilcoxon检验
log-rank检验(时序检验)--生存时间分布近似weibull分布或者属于比例风险模型时效率较高
似然比检验(likelihood ratio test)--生存时间分布近似指数分布时效率较高
wilcoxon检验--生存时间分布近似对数正态分布效率较高
survdiff使用示例
> survdiff(Surv(futime, fustat) ~ rx,data=ovarian)
Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)
N Observed Expected (O-E)^2/E (O-E)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06
Chisq= 1.1 on 1 degrees of freedom, p= 0.303
> # 用strata来控制协变量的影响
> survdiff(Surv(time, status) ~ pat.karno + strata(inst), data=lung)
Call:
survdiff(formula = Surv(time, status) ~ pat.karno + strata(inst),
data = lung)
n=224, 4 observations deleted due to missingness.
N Observed Expected (O-E)^2/E (O-E)^2/V
pat.karno=30 2 1 0.692 0.13720 0.15752
pat.karno=40 2 1 1.099 0.00889 0.00973
pat.karno=50 4 4 1.166 6.88314 7.45359
pat.karno=60 30 27 16.298 7.02790 9.57333
pat.karno=70 41 31 26.358 0.81742 1.14774
pat.karno=80 50 38 41.938 0.36978 0.60032
pat.karno=90 60 38 47.242 1.80800 3.23078
pat.karno=100 35 21 26.207 1.03451 1.44067
Chisq= 21.4 on 7 degrees of freedom, p= 0.00326
> survdiff(Surv(time, status) ~ pat.karno + sex, data=lung)
Call:
survdiff(formula = Surv(time, status) ~ pat.karno + sex, data = lung)
n=225, 3 observations deleted due to missingness.
N Observed Expected (O-E)^2/E (O-E)^2/V
pat.karno=30, sex=1 1 1 0.246 2.31e+00 2.33e+00
pat.karno=30, sex=2 1 0 0.412 4.12e-01 4.16e-01
pat.karno=40, sex=1 1 1 0.132 5.68e+00 5.72e+00
pat.karno=40, sex=2 1 0 1.204 1.20e+00 1.22e+00
pat.karno=50, sex=1 2 2 0.111 3.23e+01 3.25e+01
pat.karno=50, sex=2 2 2 0.968 1.10e+00 1.11e+00
pat.karno=60, sex=1 18 17 9.173 6.68e+00 7.14e+00
pat.karno=60, sex=2 12 10 6.064 2.56e+00 2.68e+00
pat.karno=70, sex=1 30 23 16.737 2.34e+00 2.65e+00
pat.karno=70, sex=2 11 8 9.527 2.45e-01 2.62e-01
pat.karno=80, sex=1 32 26 24.570 8.32e-02 9.91e-02
pat.karno=80, sex=2 19 13 16.311 6.72e-01 7.55e-01
pat.karno=90, sex=1 31 25 24.992 2.66e-06 3.21e-06
pat.karno=90, sex=2 29 13 24.420 5.34e+00 6.33e+00
pat.karno=100, sex=1 21 15 14.002 7.11e-02 7.91e-02
pat.karno=100, sex=2 14 6 13.131 3.87e+00 4.25e+00
Chisq= 66.1 on 15 degrees of freedom, p= 2.17e-08
anova
计算一个或多个拟合模型的方差(或偏差)表的分析
mod1<-survreg(Surv(time, status) ~ ph.ecog + age + sex, data=lung,dist = "weibull")
mod2<-survreg(Surv(time, status) ~ ph.ecog + age + sex+ph.karno*pat.karno, data=lung,dist = "weibull")
anova(mod1,mod2,test="Chisq")
Terms Resid. Df -2*LL Test Df Deviance Pr(>Chi)
1 ph.ecog + age + sex 222 2264.877 NA NA NA
2 ph.ecog + age + sex + ph.karno * pat.karno 215 2209.372 = 7 55.50527 1.183848e-09
library(MASS)
# 简洁模型更好
stepAIC(mod1)
stepAIC(mod2)




