left 1 Codeforces Round 920 (Div. 3)
D.
贪心思路初步是对的
最大配最小
但是，最小也可能配最小
比如 999 1000
1 2
这个例子，就是最小配最小
还是极端到极端的问题，两个极端都要考虑
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
void solve() {
int n,m;cin>>n>>m;
vector<int>a(n+1);
for(int i=1;i<=n;i++)cin>>a[i];
sort(a.begin()+1,a.end());
vector<int>b(m+1);
for(int i=1;i<=m;i++)cin>>b[i];
sort(b.begin()+1,b.end());
int d=0;
int l1=1,r1=n,l2=1,r2=m;
while(l1<=r1){
int l=abs(a[l1]-b[r2]);
int r=abs(a[r1]-b[l2]);
if(l>r){
d+=l;
l1++;
r2--;
}else {
d+=r;
l2++;
r1--;
}
}
cout<<d<<'\n';
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int left=1;
cin>>left;
while(left--){
solve();
}
}
E.
A和B每走一步横坐标一定变化
所以若A的横坐标大等于B的，那么一定平局
A先手，我们可以知道A与B的横坐标之差如果是奇数，是A吃B。
A走 差/2+1，B走 差/2步
走完后A、B一定在同一行
那么再判在不在同一列
最优，一定是往一个一个方向走（由走路特点决定）
注意棋盘有边界，到边界则只能走竖直方向
判吃方横向位置能否追上被吃方即可
debug：
我算了A和B向左向右最远走了多少，然后看差值是否为0，即是否相遇
这样若棋盘够长，吃方可能比被吃方走得多
所以应该是判吃方在两个方向上能否比被吃方走得更远
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
void solve() {
int h,w,xa,ya,xb,yb;cin>>h>>w>>xa>>ya>>xb>>yb;
if(xa>=xb){
cout<<"Draw"<<'\n';
return ;
}
int hc=abs(xa-xb);
if(hc&1){
int step=hc/2;
int b1=min(w,yb+step),b2=max(1ll,yb-step),a1=min(w,ya+step+1),a2=max(1ll,ya-step-1);
//int c=min({abs(b1-a1),abs(b1-a2),abs(b2-a1),abs(b2-a2)});
if(a2<=b2&&a1>=b1) {
cout << "Alice" << '\n';
return;
}else {
cout << "Draw" << '\n';
return;
}
}else{
int step=hc/2;
int b1=min(w,yb+step),b2=max(1ll,yb-step),a1=min(w,ya+step),a2=max(1ll,ya-step);
// int c=min({abs(b1-a1),abs(b1-a2),abs(b2-a1),abs(b2-a2)});
if(b2<=a2&&b1>=a1) {
cout << "Bob" << '\n';
return;
}else {
cout << "Draw" << '\n';
return;
}
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int left=1;
cin>>left;
while(left--){
solve();
}
}
F.
根号分治
一共有n个数，每次最多选择n/d个数
那么若d很大，则时间复杂度并不高
若d很小，时间复杂度很高
所以考虑根号分治
d大等于根号n时，直接暴力计算
d小于等于根号时，预处理两个后缀和
注意，普通的后缀和每个数只计数了一次
我们这里有权值，所以对于后缀和再做一次后缀和
那么越靠后的数，被加的次数越多，权值就体现出来了
以下是具体的例子：
原： 1 1 1
前缀和： 3 2 1
前缀和 6 3 1
6的组成：第一个11，第二个12，第三个1*3
d2[i][d]以i为第一个且i的权值为1，i+d为第2个，且权值为2...
i+d及i+d之后的，有公共权值为d，然后是1,2,3...的权值
附图：
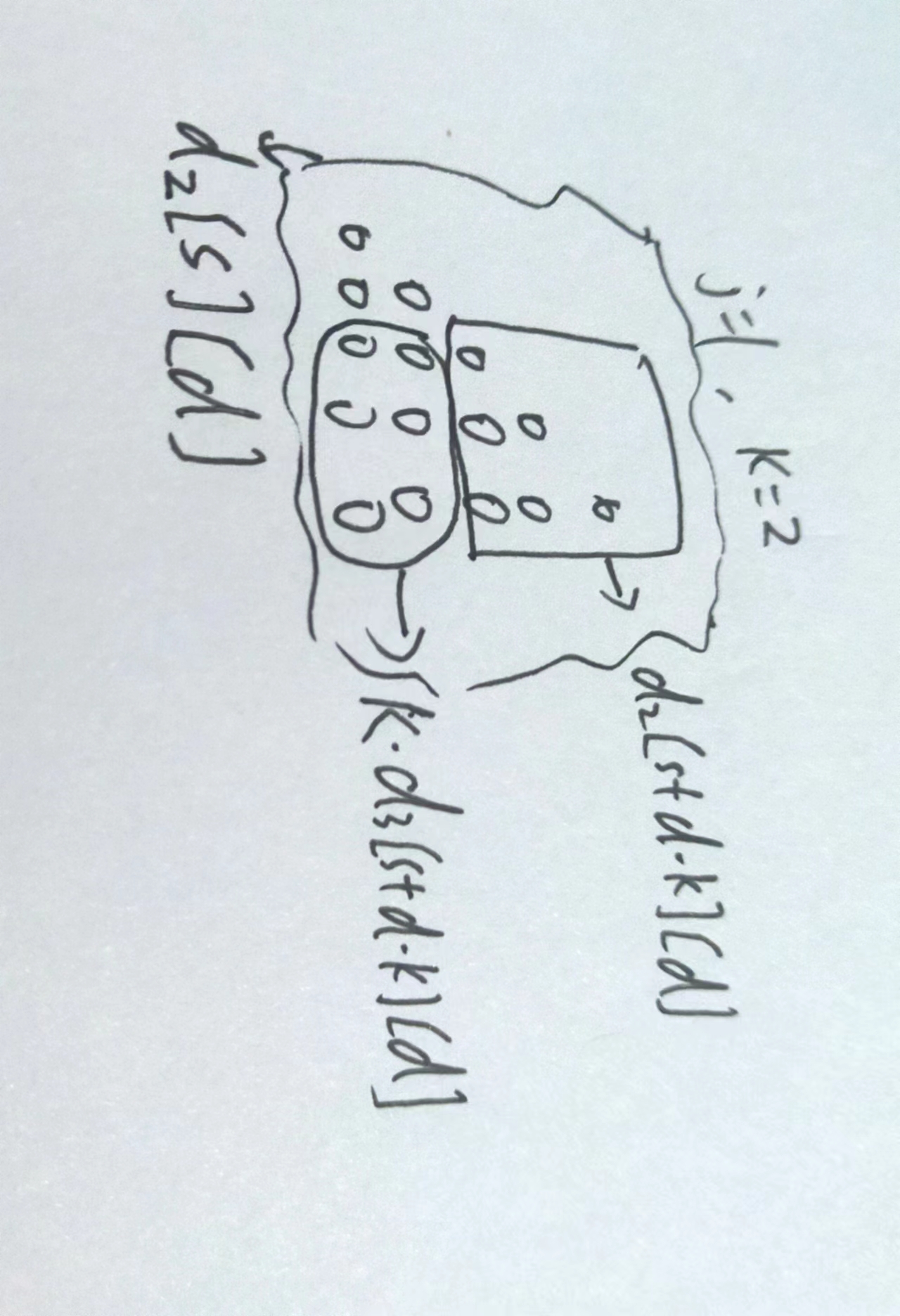
代码：
#include<bits/stdc++.h>
using namespace std;
long long t,n,q,a[100010],d3[100010][320],d2[100010][320];
signed main(){
cin>>t;
for(int l=1;l<=t;l++){
cin>>n>>q;
int sq=sqrt(n);
for(int i=1;i<=n+sq;i++) for(int j=1;j<=319;j++) d3[i][j]=0,d2[i][j]=0;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=n;i>=1;i--) for(int j=1;j<=sq;j++) d3[i][j]=d3[i+j][j]+a[i];
for(int i=n;i>=1;i--) for(int j=1;j<=sq;j++) d2[i][j]=d2[i+j][j]+d3[i][j];
for(int j=1;j<=q;j++){
int s,d,k;
cin>>s>>d>>k;
if(d>=sq){
long long ans=0;
for(int i=1;i<=k;i++) ans+=a[s+(i-1)*d]*i;
cout<<ans<<" ";
}
else cout<<d2[s][d]-d2[s+d*k][d]-k*d3[s+d*k][d]<<endl;
}
cout<<endl;
}
return 0;
}
G.
把这个奇形怪状的范围看成仅由行或仅由列组成即可
计算时间复杂大的重要性
O（nmsqrt）
行少就枚举行，列少就枚举列
这里用的二维前缀和
对于每个点枚举4种情况
#include <bits/stdc++.h>
using namespace std;
string g[100010];
vector<int> pre[100010];
int gt(int x1,int y1,int x2,int y2)
{
return pre[x2][y2]-(x1==0?0:pre[x1-1][y2])-(y1==0?0:pre[x2][y1-1])+(x1==0||y1==0?0:pre[x1-1][y1-1]);
}
void solve() {
int n,m,k;
cin>>n>>m>>k;
for(int i = 0;i<n;i++) {cin>>g[i];pre[i].resize(m);}
pre[0][0] = (g[0][0]=='#');
for(int i = 0;i<n;i++)
{
for(int j = 0;j<m;j++)
{
if(i==0&&j==0) continue;
if(i==0) pre[i][j] = pre[i][j-1]+(g[i][j]=='#');
else if(j==0) pre[i][j] = pre[i-1][j]+(g[i][j]=='#');
else pre[i][j] = pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+(g[i][j]=='#');
}
}
int ans = 0;
if(n<m) //暴力枚举行.
{
for(int i = 0;i<n;i++)
{
for(int j = 0;j<m;j++)
{
//枚举四种方式
int sum = 0;
for(int l = 0;l<=k;l++)
{
int row = i-l,col = min(j+k-l,m-1);
if(row<0) break;
sum+=gt(row,j,row,col);
}
ans = max(ans,sum);
sum = 0;
for(int l = 0;l<=k;l++)
{
int row = i+l,col = min(j+k-l,m-1);
if(row>=n) break;
sum+=gt(row,j,row,col);
}
ans = max(ans,sum);
sum = 0;
for(int l = 0;l<=k;l++)
{
int row = i+l,col = max(j-k+l,0);
if(row>=n) break;
sum+=gt(row,col,row,j);
}
ans = max(ans,sum);
sum = 0;
for(int l = 0;l<=k;l++)
{
int row = i-l,col = max(j-k+l,0);
if(row<0) break;
sum+=gt(row,col,row,j);
}
ans = max(ans,sum);
}
}
} else //暴力枚举列.
{
for(int i = 0;i<n;i++)
{
for(int j = 0;j<m;j++)
{
//枚举四种方式
int sum = 0;
for(int l = 0;l<=k;l++)
{
int col = j+l,row = max(0,i-k+l);
if(col>=m) break;
sum+=gt(row,col,i,col);
}
ans = max(ans,sum);
sum = 0;
for(int l = 0;l<=k;l++)
{
int col = j+l,row = min(n-1,i+k-l);
if(col>=m) break;
sum+=gt(i,col,row,col);
}
ans = max(ans,sum);
sum = 0;
for(int l = 0;l<=k;l++)
{
int col = j-l,row = min(n-1,i+k-l);
if(col<0) break;
sum+=gt(i,col,row,col);
}
ans = max(ans,sum);
sum = 0;
for(int l = 0;l<=k;l++)
{
int col = j-l,row = max(0,i-k+l);
if(col<0) break;
sum+=gt(row,col,i,col);
}
ans = max(ans,sum);
}
}
}
cout<<ans<<'\n';
}
int main(){
int left;
cin>>left;
while(left--){
solve();
}
return 0;
}
