hey_left 7 Codeforces Round 886 (Div. 4) 续

题目链接

F.

记录下出现的数字和个数
注意放置陷阱的位置1-n都有可能
然后遍历1-n，对每个数进行因子分解，对于在因子的位置上有青蛙的，加上青蛙的个数，取最大即可

#include <bits/stdc++.h>
using namespace std;

#define int long long
const int N=2e5+10;

void solve(){
    int n;cin>>n;
    map<int,int>mp;
    map<int,int>be;
    for(int i=1,x;i<=n;i++){
        cin>>x;
        be[x]++;
    }
//    for(auto t:be){
//        cout<<t.first<<' '<<t.second<<'\n';
//    }
    for(int i=1;i<=n;i++){
        int val=i;
        for(int j=1;j*j<=val;j++){
            if(val%j==0){
                if(be[j])
                    mp[val]+=be[j];
                if(val/j!=j){
                    if(be[val/j]) {
                        mp[val] += be[val/j];
                       // cout<<"be[j]="<<be[j]<<'\n';
                    }
                }
            }
        }
    }
    int ma=0;
    for(auto t:mp){
        if(t.first<=n&&t.second>ma){
            ma=t.second;
        }
    }
    cout<<ma<<'\n';
}

signed main(){
    int hey_left=1;
    cin>>hey_left;
    while(hey_left--) {
        solve();
    }
    return 0;
}

G.

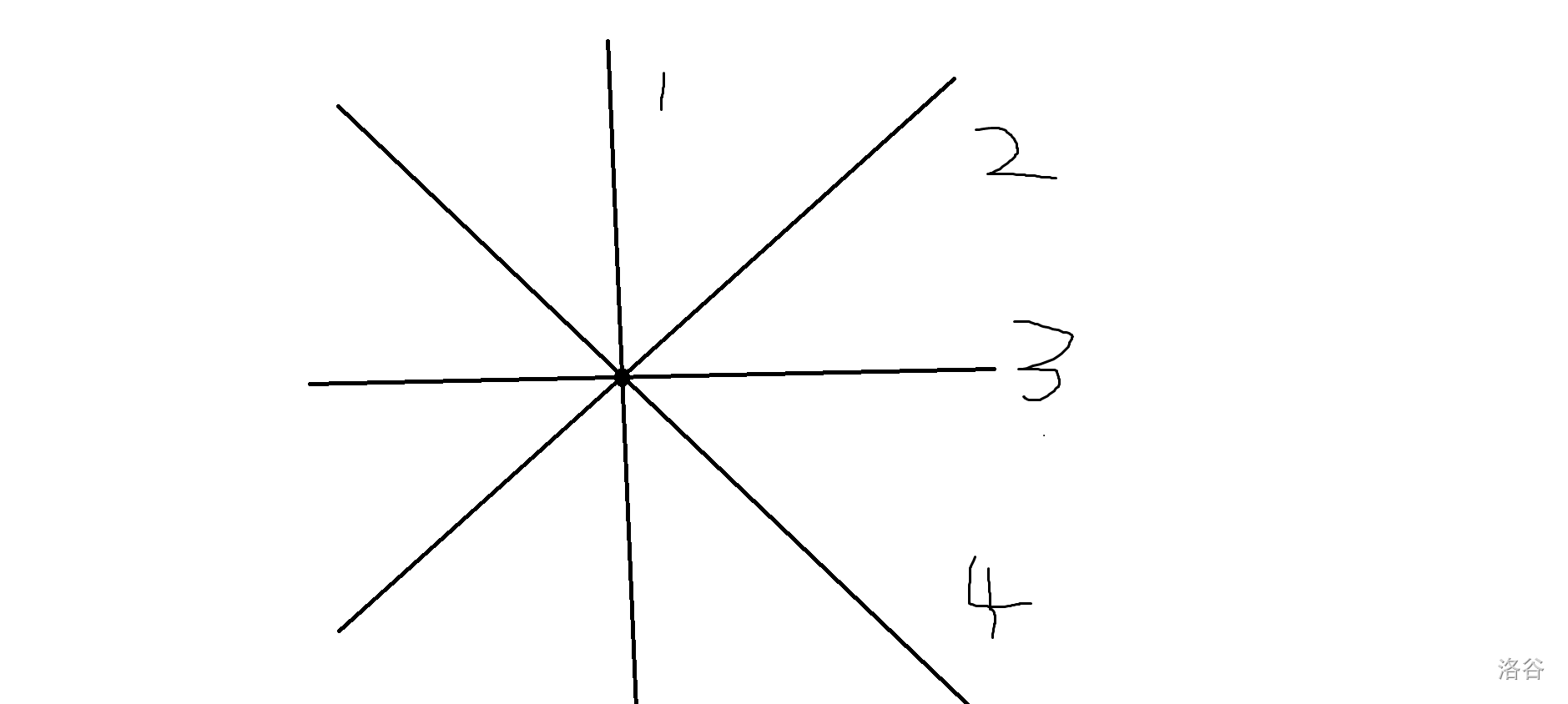
直线上点的特性：
直线1：x1=x0
直线2：x2-x0=y2-y0,即x0-y0=x2-y2
直线3：y3=y0
直线4：x4-x0=y0-y4,即x0+y0=x4+y4

自己做的时候已经想到了x2-x0=y2-y0
以为一定要两个数比较才能确定，n方复杂度认为做不了
其实移下项就好了

然后记录答案的时候，最好是分开算，并且点数大于1

#include <bits/stdc++.h>
using namespace std;

const int N=2e5+10;

#define int long long
map<int,int>tx,ty,tbx,tnx;
pair<int,int>a[N];
void solve(){
    tx.clear();ty.clear();tbx.clear();tnx.clear();
    int n;cin>>n;
    for(int i=1,x,y;i<=n;i++){
        cin>>x>>y;
        a[i].first=x;a[i].second=y;
        tx[x]++;
        ty[y]++;
        tbx[{x-y}]++;
        tnx[{x+y}]++;
    }
    int sum=0;
    for(int i=1;i<=n;i++){
        int xx=a[i].first,yy=a[i].second;
        if(tx[xx]>1)sum+=tx[xx]-1;
        if(ty[yy]>1)sum+=ty[yy]-1;
        if(tbx[{xx-yy}])sum+=tbx[{xx-yy}]-1;
        if(tnx[{xx+yy}])sum+=tnx[{xx+yy}]-1;
    }
    cout<<sum<<'\n';
}

signed main(){
    int hey_left=1;
    cin>>hey_left;
    while(hey_left--) {
        solve();
    }
    return 0;
}

H.

有几点导致没做出来：
1.建双向边
原来觉得从小到大的线性关系就建的单向边
2.按连通块去遍历
原来按从1-n的顺序，会出现时序问题
3.总想着从小到大线性地确定唯一关系

正解：
首先建双向边
对于每个连通块，确定一点，算出其他点的位置，注意判合法，这里用的bfs遍历连通块

#include <bits/stdc++.h>
using namespace std;

#define int long long

void solve(){
    int n,m;cin>>n>>m;
    vector<vector<pair<int,int>>>g(n+1);
    for(int i=1,a,b,d;i<=m;i++){
        cin>>a>>b>>d;
        g[a].push_back({b,-d});
        g[b].push_back({a,d});
    }
    vector<int>dist(n+1,LLONG_MIN);
    for(int i=1;i<=n;i++){
        if(dist[i]!=LLONG_MIN)continue;
        dist[i]=0;
        queue<int>q;
        q.push(i);
        while(q.size()){
            int t=q.front();q.pop();
            for(int j=0;j<g[t].size();j++){
                int k=g[t][j].first,dis=g[t][j].second;
                if(dist[k]!=LLONG_MIN){
                    if(dist[k]!=dist[t]+dis){
                        cout<<"NO"<<'\n';
                        return ;
                    }
                }else{
                    dist[k]=dist[t]+dis;
                    q.push(k);
                }
            }
        }
    }
    cout<<"YES"<<'\n';
}

signed main(){
    int hey_left=1;
    cin>>hey_left;
    while(hey_left--){
        solve();
    }
}