从最简单的感知器学习到的一些有趣的现象
看了一些深度学习神经网络的视频，最近有了一点新的体会，在google的一个小工具上，地址:http://playground.tensorflow.org 一个神经网络训练的模拟器，发现了一些有意思的事情，有了些新的体会
这里分享给大家。
1 权值，刚开始都是设置的随机初始值，但是随着训练的深入，你会发现权值变化的一些规律，这里一二分类为列，某些对最终分类帮助性大的因素即输入的权值会越来越大，而那些对分类作用小的因素，甚至对分类起反作用的因素的权值会逐渐变得很小，或者为负值，有些同学会问权值之和是不是为1，显然不是，这里是不是和概率论的知识混淆了，下面一图来展示
我们的初始值大概是这个样子：对于这个数据集有点类似异或的关系，但是观察坐标轴你会发现这个图的正中间的坐标原点是（0，0）所以它与异或有些不同但同样不是最简单的感知器即两个输入能进行分类的，所以我们这里采用改进的感知器，另外增加了三个元素即增加了一些非线性的因素。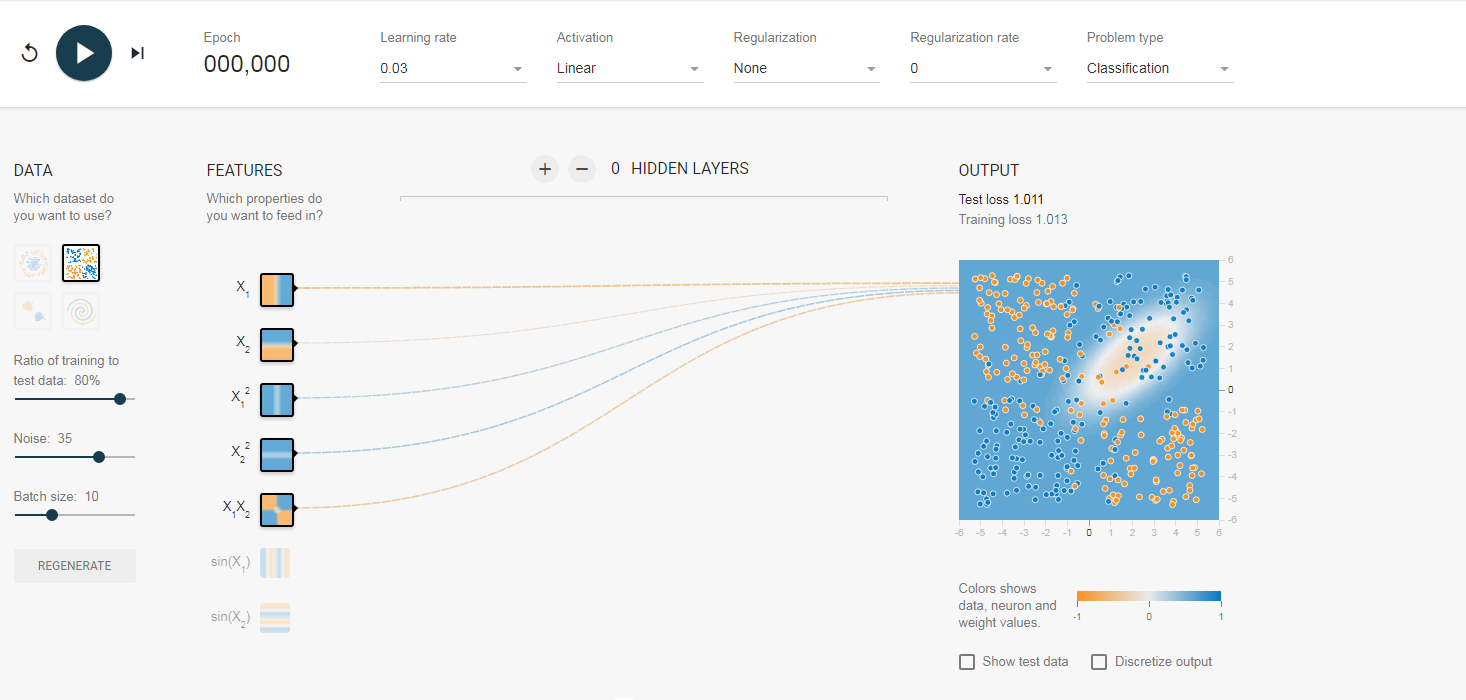
大家先看这个小图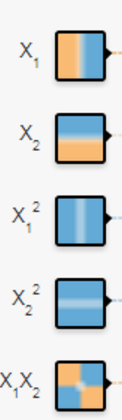
有没有发现什么，对于x1它是相当于数据集（1，3）（3，5）（3，7）等等的x值，而小图也显示它将整个图分为ie左右两半，而对于x2则是数据集中的y值，它将图分为上下两半，其他的都类似，这样我们来看最后一个因素，x1*x2,这个会决定什么，查看它的小图，你会发现它几乎已经将数据集分成了最终的效果图，大概就是x1*x2为负值是一类，x1*x2是正值为另一类，这里大家可以看图来理解。
所以现在大家可以来预测了，后面我们开始训练后，随着训练次数的迭代，那些输入的权值会越来越大，那些则会削弱。我们来看图，这里我们列举多个结果图，它们的初始全职不同，但是训练结果对于权值的分布是类似的，（另外跟大家解释一下，神经元之前的连线代表权值，蓝色为正，黄色为负，越粗绝对值越大）：
初始值：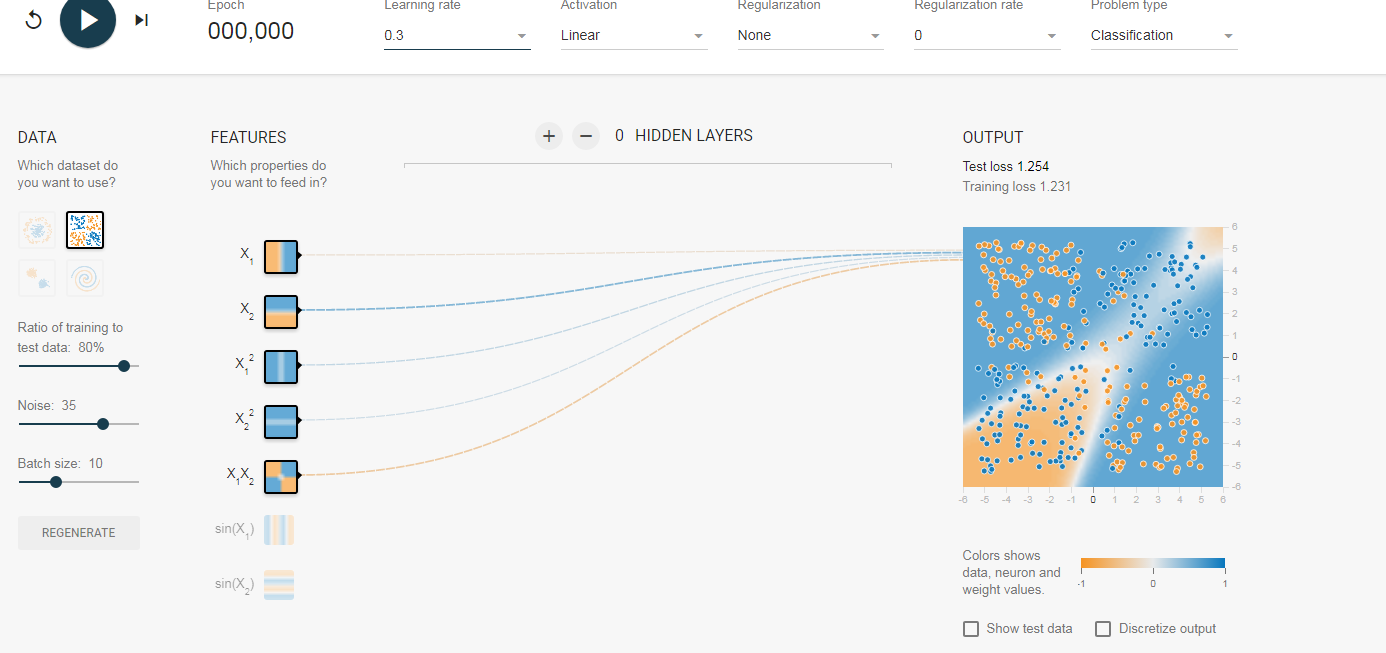
结果：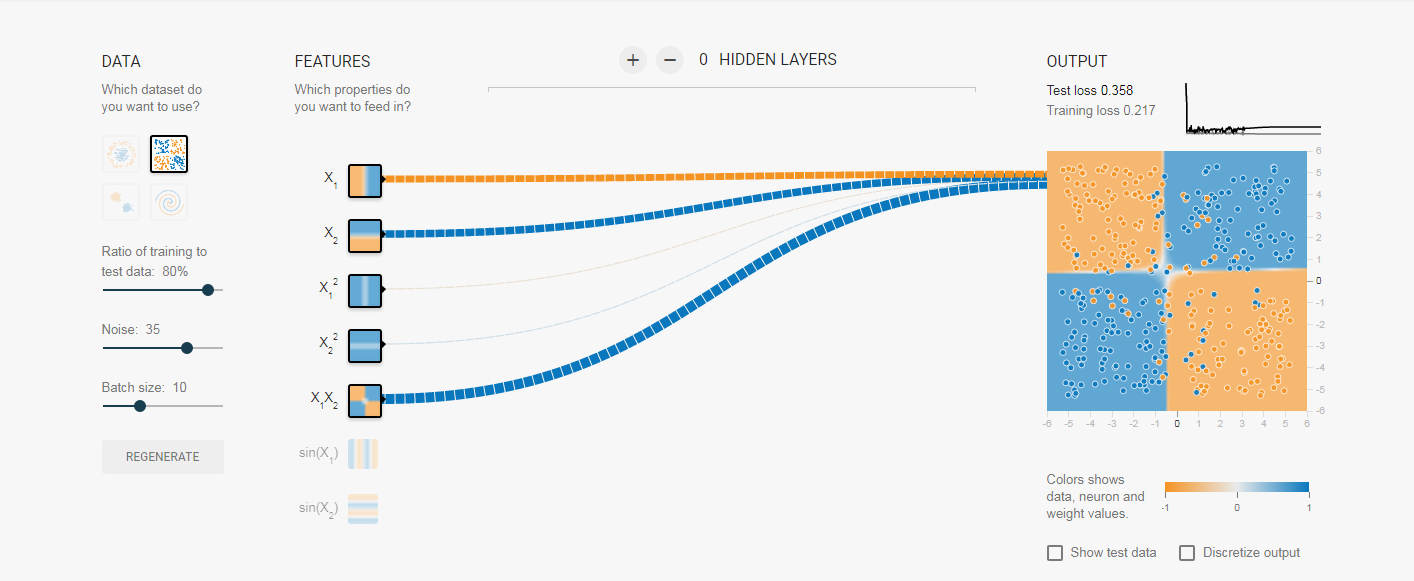
初始值：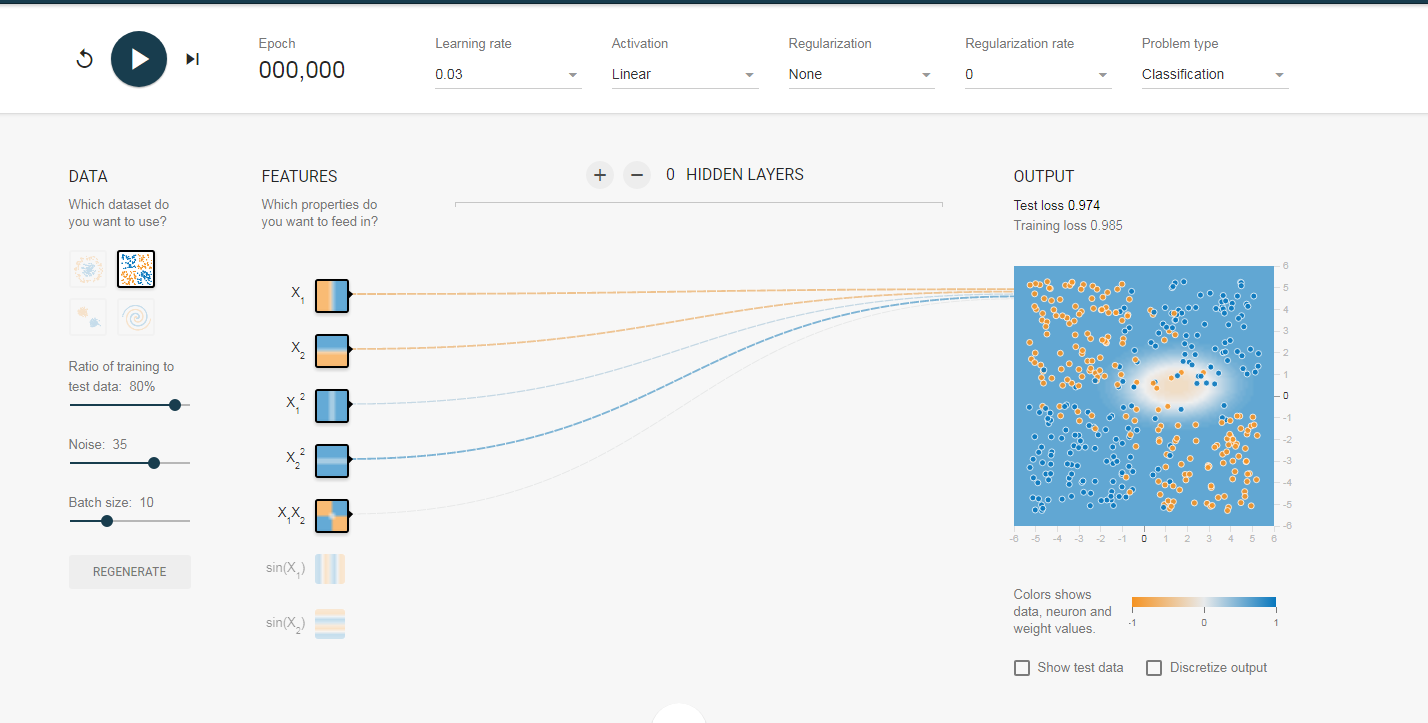
结果：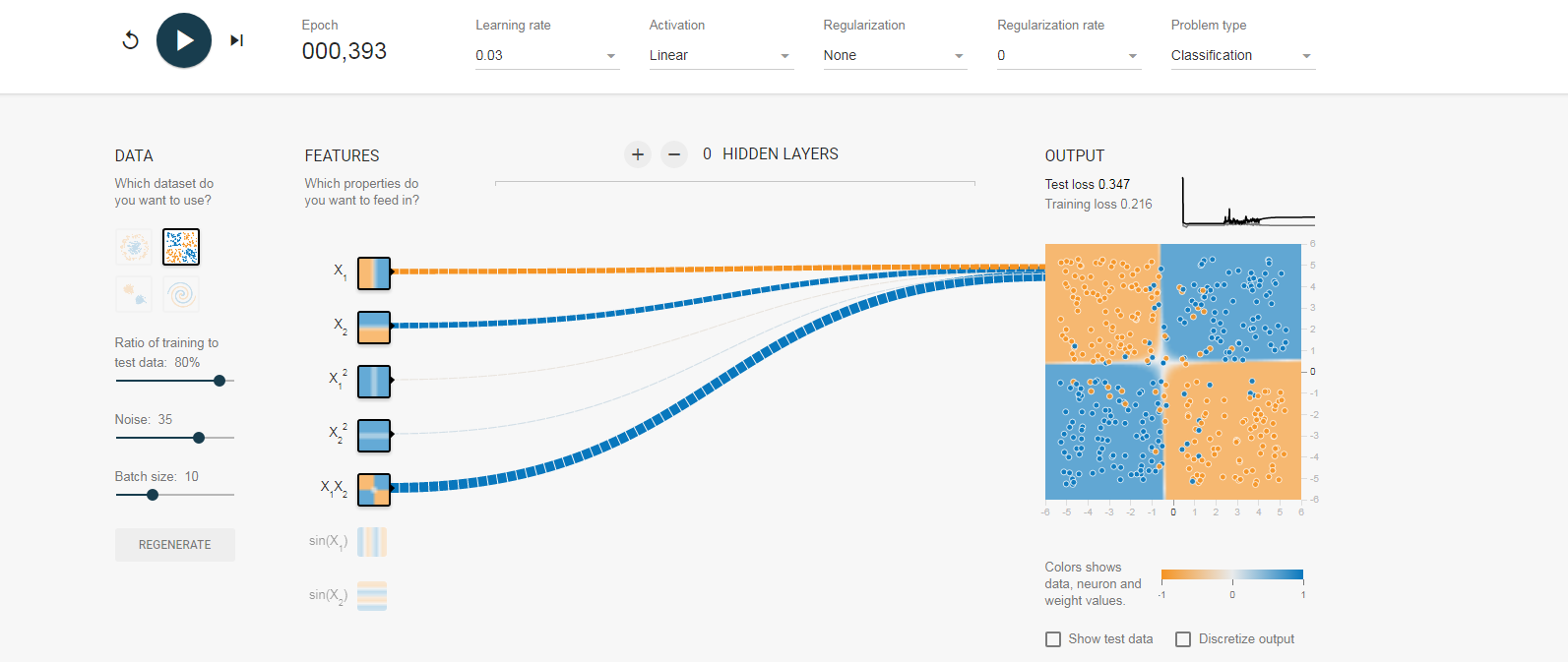
对于线性可分的，我这里也给一个例子，大家可以看出来，凭借x1和x2已经可以将数据分开了，其他三个因素几乎用不着：大家看权值：
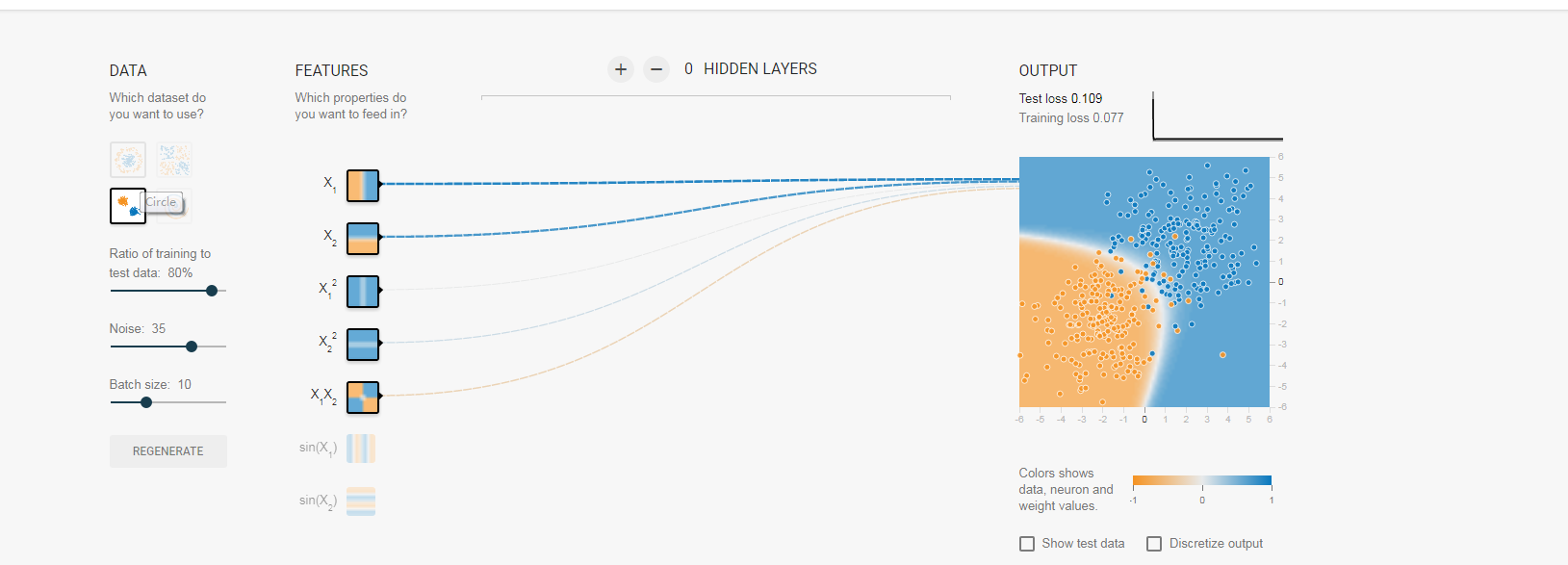
大家可以看出来全职变化的规律了吧。
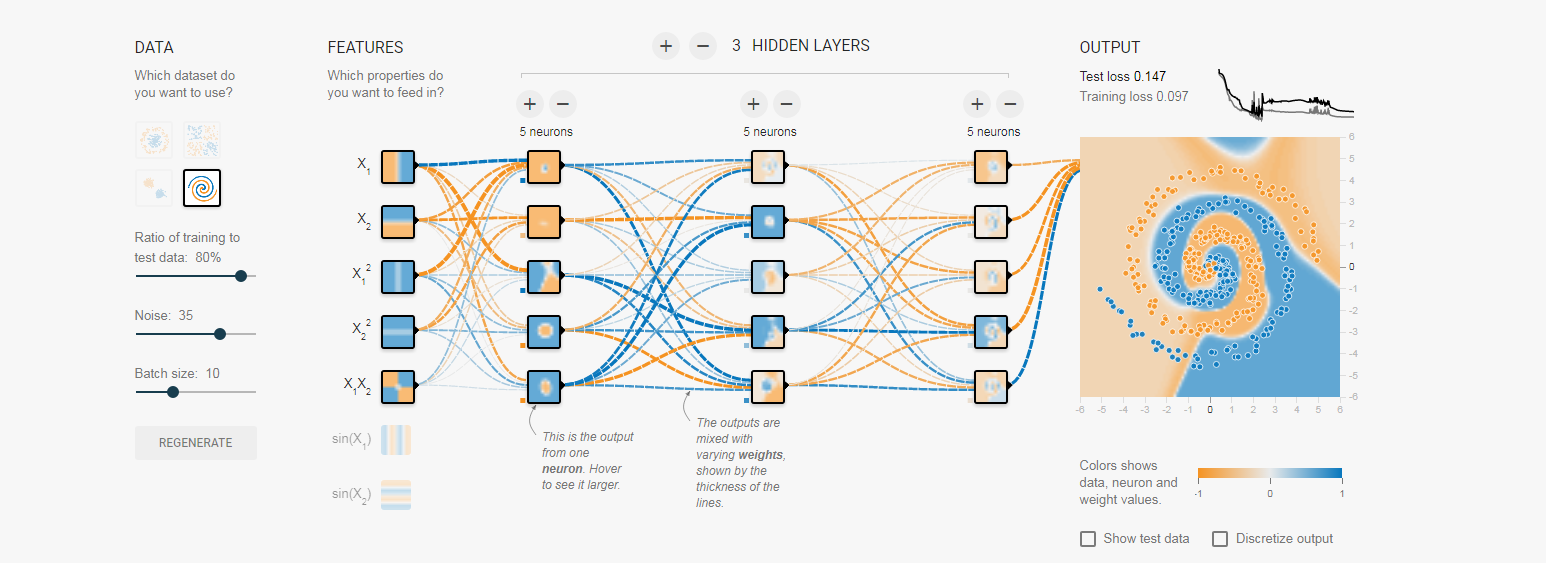
2，对于多层神经元的模型，神经元的层次越深，这个神经元“考虑的因素越多”，就像我们俗话说的，考虑全面，将各种因素考虑在内，事情才能办的更好，这里同样对于我们的输出来说，层次越多，综合各种因素越强，对于训练集来说最终的分类结果也会越好，这也是对简单的问题，采用过于复杂的模型对导致过拟合的原因。
同样来张图向大家展示，大家可以逐层次的看神经元的小图来与输入，和输出比较：
