经典算法-（六）老鼠走迷宫

问题描述：

给定一个二维数组，数组中2表示墙壁，0表示通路，由此数组可展示为一个迷宫图。给定入口位置和出口位置，判断之间是否存在通路并显示出走出迷宫的道路。

问题解答：

实际上是使用回溯算法求解该问题，就是在上下左右四个方向试探，倘若有路则走一步，在新的位置继续在四个位置试探，并且对走过的路进行标记，倘若走到死胡同里，则退回上一步再来试探，以此类推，类似于图的深度优先算法，使用递归来实现。

java实现：

package a;
import java.math.BigInteger;
import java.util.*;
public class Main{     
    public static  void main(String[] args)  {  
        System.out.println("请输入一数来开始");
        Scanner cin = new Scanner(System.in);       
        while(cin.hasNext()){
          String n=cin.next();
          int[][] maze =new int [][] {
                {2,2,2,2,2,2,2,2,2},  
                {2,0,0,0,0,0,0,0,2},  
                {2,0,2,2,0,2,2,0,2},  
                {2,0,2,0,0,2,0,0,2},  
                {2,0,2,0,2,0,2,0,2},  
                {2,0,0,0,0,0,2,0,2},  
                {2,2,0,2,2,0,2,2,2},  
                {2,0,0,0,0,0,0,0,2},  
                {2,2,2,2,2,2,2,2,2}  
                };   
             xun(maze,1,1);
                
 }
        cin.close();      
    }
    static void xun(int[][] a,int i,int j) {
               a[i][j]=1; 
            if(i==7&&j==7)
            { System.out.println("打印一波：--------------");
            System.out.println();
                for(int m=0;m<9;m++) {
                    for (int n=0;n<9;n++) {
                        System.out.print(a[m][n]+" ");
                    }
                    System.out.println();
                }
            }
            if(a[i][j+1]==0) {
                  xun(a,i,j+1);
                }
            if(a[i+1][j]==0) {
                    xun(a,i+1,j);    
            }
             if(a[i-1][j]==0) {
                xun(a,i-1,j);    
            }
             if(a[i][j-1]==0) {
                xun(a,i,j-1);    
            }
             a[i][j]=0;
    }
}

运算结果：

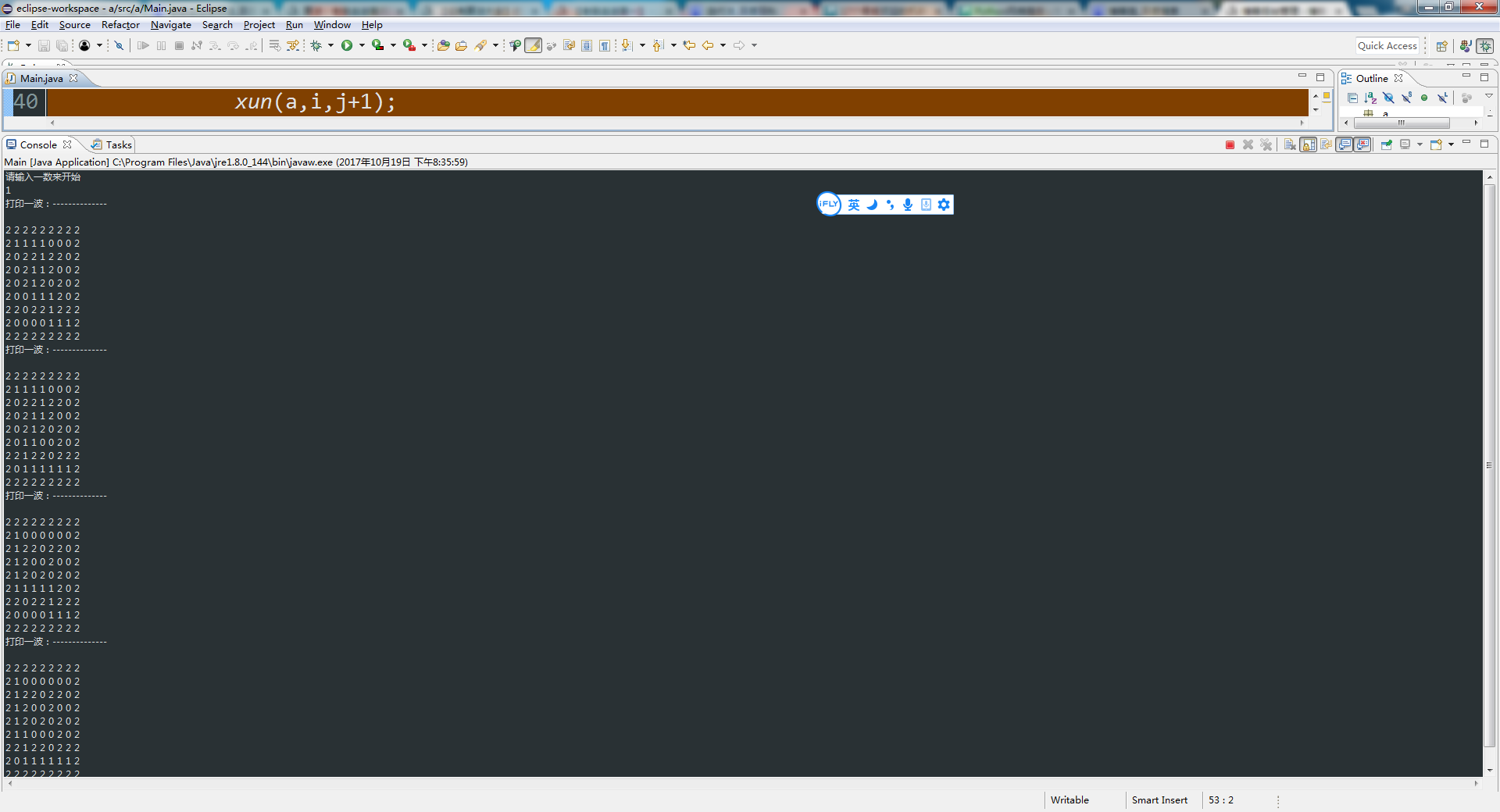
点评：

现在的代码是将所有可能的路线都打印出来了，稍微修改下可以实现打印一种结果，打印了所有的结果正是体现了回溯法可实现遍历出所有可能的答案。

顺便附上打印一种结果的实现代码 ：

c++实现：

#include <stdio.h>
#include <stdlib.h>

int visit(int , int );

int maze[7][7] = {
    {2, 2, 2, 2, 2, 2, 2},
    {2, 0, 0, 0, 0, 0, 2},
    {2, 0, 2, 0, 2, 0, 2},
    {2, 0, 0, 2, 0, 2, 2},
    {2, 2, 0, 2, 0, 2, 2},
    {2, 0, 0, 0, 0, 0, 2},
    {2, 2, 2, 2, 2, 2, 2} 
};

int startI = 1, startJ = 1;
int endI = 5, endJ = 5;
int success = 0;

int main(void)
{
    int i, j;

    printf("显示迷宫：\n");
    for(i = 0; i < 7; i++)
    {
        for(j = 0; j < 7; j++)
        {
            if(maze[i][j] == 2)
                printf("#");
            else
                printf(" ");
        }
        printf("\n");
    }
    
    if(visit(startI, startJ) == 0)
        printf("\n没有找到出口!\n");
    else
    {
        printf("\n显示路径：\n");
        for(i = 0; i < 7; i++)
        {
            for(j = 0; j < 7; j++)
            {
                if(maze[i][j] == 2)
                    printf("#");
                else if(maze[i][j] == 1)
                    printf("1");
                else
                    printf(" ");
            }
            printf("\n");        
        }
    }
    return 0;
} 

int visit(int i, int j)
{
    maze[i][j] = 1;
    
    if(i == endI && j == endJ)
        success = 1;
        
    if(success != 1 && maze[i][j+1] == 0)
        visit(i, j+1); 
    if(success != 1 && maze[i+1][j] == 0)
        visit(i+1, j);
    if(success != 1 && maze[i][j-1] == 0)
        visit(i, j-1);
    if(success != 1 && maze[i-1][j] == 0)
        visit(i-1, j);
        
    if(success != 1)
        maze[i][j] = 0; 
    return success;
}