Description
You are to write a program to read different formulas and determine whether or not they are arithmetically equivalent.
Input
- Single letter variables (case insensitive).
- Single digit numbers.
- Matched left and right parentheses.
- Binary operators +, - and * which are used for addition, subtraction and multiplication respectively.
- Arbitrary number of blank or tab characters between above tokens.
Note: Expressions are syntactically correct and evaluated from left to right with equal precedence (priority) for all operators. The coefficients and exponents of the variables are guaranteed to fit in 16-bit integers.
Output
Sample Input
3 (a+b-c)*2 (a+a)+(b*2)-(3*c)+c a*2-(a+c)+((a+c+e)*2) 3*a+c+(2*e) (a-b)*(a-b) (a*a)-(2*a*b)-(b*b)
Sample Output
YES YES NO
解题思路:我的程序是把每个 'a'--'z' 的字母分别hash成0--25 再把每个 'A'--'Z' 的字母分别hash成0--25
给出两个数学式子判断其结果是否相等。
解法:
1,用栈将表达式转换成为后缀式,然后计算后缀表达式的只判断其是否相等。
2,其中有一个问题就是字母转换之后如何算其值来代表其字母的值,我用的是(int)s1[i]直接将其ASCII作为数值对待,结果也AC了(看来这个 题只是判断两个表达式是否在数值上是等价的而不是判断两个公式是否等价 比如说:(b-a+c)*2 与 (1+c)*2也相等,但是如果作为公式的话这两个是不相等的)。
规则
中缀表达式a + b*c + (d * e + f) * g,其转换成后缀表达式则为a b c * + d e * f + g * +。
转换过程需要用到栈,具体过程如下:
1)如果遇到操作数,我们就直接将其输出。
2)如果遇到左括号,我们直接将其放入到栈中。
3)如果遇到一个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为止。注意,左括号只弹出并不输出。
4)如果遇到任何其他的操作符,如(“+”, “*”,“-“)等,从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后,才将遇到的操作符压入到栈中。有一点需要注意,只有在遇到" ) "的情况下我们才弹出" ( ",其他情况我们都不会弹出" ( "。优先级从大到小顺序为:" * " 与 " / "," + " 与 " - ","(",也就是说" ( "优先级最低。
5)如果我们读到了输入的末尾,则将栈中所有元素依次弹出。
规则规则很多,还是用实例比较容易说清楚整个过程。以上面的转换为例,输入为a + b * c + (d * e + f)*g,处理过程如下:
1)首先读到a,直接输出。
2)读到“+”,将其放入到栈中。
3)读到b,直接输出。
此时栈和输出的情况如下:

4)读到“*”,因为栈顶元素"+"优先级比" * " 低,所以将" * "直接压入栈中。
5)读到c,直接输出。
此时栈和输出情况如下:

6)读到" + ",因为栈顶元素" * "的优先级比它高,所以弹出" * "并输出, 同理,栈中下一个元素" + "优先级与读到的操作符" + "一样,所以也要弹出并输出。然后再将读到的" + "压入栈中。
此时栈和输出情况如下:

7)下一个读到的为"(",所以直接放入到栈中。
8)读到d,将其直接输出。
此时栈和输出情况如下:

9)读到" * ",由于只有”(“的优先级最低,遇到" ) "的时候左括号"("才会弹出,所以" * "压入栈中。
10)读到e,直接输出。
此时栈和输出情况如下:
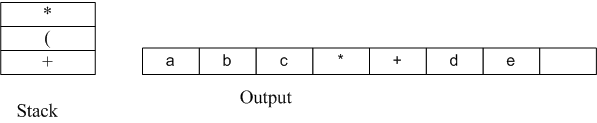
11)读到" + ",弹出" * "并输出,然后将"+"压入栈中。
12)读到f,直接输出。
此时栈和输出情况:

13)接下来读到“)”,则直接将栈中元素弹出并输出直到遇到"("为止。这里右括号前只有一个操作符"+"被弹出并输出。

14)读到" * ",压入栈中。读到g,直接输出。

15)此时输入数据已经读到末尾,栈中还有两个操作符“*”和" + ",直接弹出并输出。

至此整个转换过程完成。程序实现代码后续再补充了。
然后是后缀表达式求值后缀表达式也叫逆波兰表达式,其求值过程可以用到栈来辅助存储。假定待求值的后缀表达式为:6 5 2 3 + 8 * + 3 + *,则其求值过程如下:
1)遍历表达式,遇到的数字首先放入栈中,此时栈如下所示:
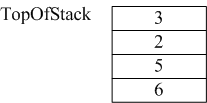
2)接着读到“+”,则弹出3和2,执行3+2,计算结果等于5,并将5压入到栈中。
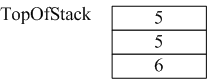
3)读到8,将其直接放入栈中。
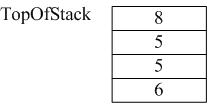
4)读到“*”,弹出8和5,执行8*5,并将结果40压入栈中。而后过程类似,读到“+”,将40和5弹出,将40+5的结果45压入栈...以此类推。最后求的值288。
借鉴了高人的解题思路,自己不怎么表达的清楚
程序代码:
#include<iostream> #include <cstdio> #include<cstring> #define N 100 using namespace std; int calculate(char s[],int t,int n) //计算 { if(n<t) return 0; if(n==t) { if(s[t]>='A' && s[t]<='Z') return (s[t]-'A'); else if(s[t]>='a' && s[t]<='z') return (s[t]-'a'); else return s[t]-'0'; } int f1=-1,f2=-1; //f1 : '+' 或者是 '-'的位子;f2 : '*'的位子 int kuohao=0; for(int i=t;i<=n;i++) { if(s[i]=='(') kuohao++; else if(s[i]==')') kuohao--; else if((s[i]=='+' || s[i]=='-') && kuohao==0) f1=i; else if(s[i]=='*' && kuohao==0) f2=i; } if(f1<0 && f2<0) return calculate(s,t+1,n-1); if(f1>0) { if(s[f1]=='+') return calculate(s,t,f1-1)+calculate(s,f1+1,n); else return calculate(s,t,f1-1)-calculate(s,f1+1,n); } else return calculate(s,t,f2-1)*calculate(s,f2+1,n); } void g(char s[]) { char *p=s; char temp[N],*p1=temp; while(*p!='\0') { while(((*p==' ') ||(*p=='\t')) && (*p!='\0')) *p++; *p1=*p; p1++; p++; } *p1='\0'; strcpy(s,temp); } int main() { int t; scanf("%d",&t);getchar(); while(t--) { char str1[N],str2[N]; gets(str1); gets(str2); g(str1); g(str2); int a=calculate(str1,0,strlen(str1)-1); int b=calculate(str2,0,strlen(str2)-1); if(a==b)cout<<"YES\n"; else cout<<"NO\n"; } return 0; }



