分解合集（LU分解/谱分解(特征分解)/cholesky分解/QR分解/奇异值分解

LU分解

将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积

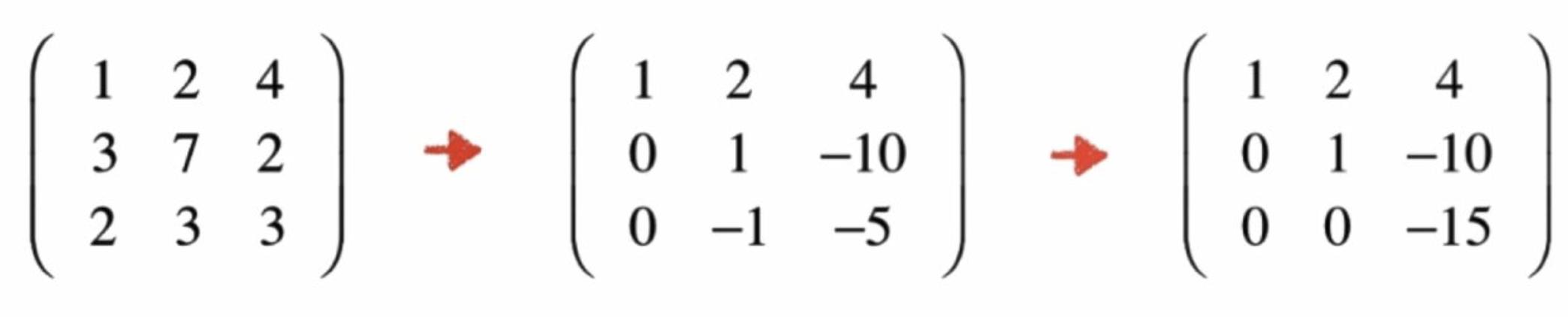
 利用高斯消去法将矩阵化为上三角形矩阵U，消去过程中左乘初等矩阵

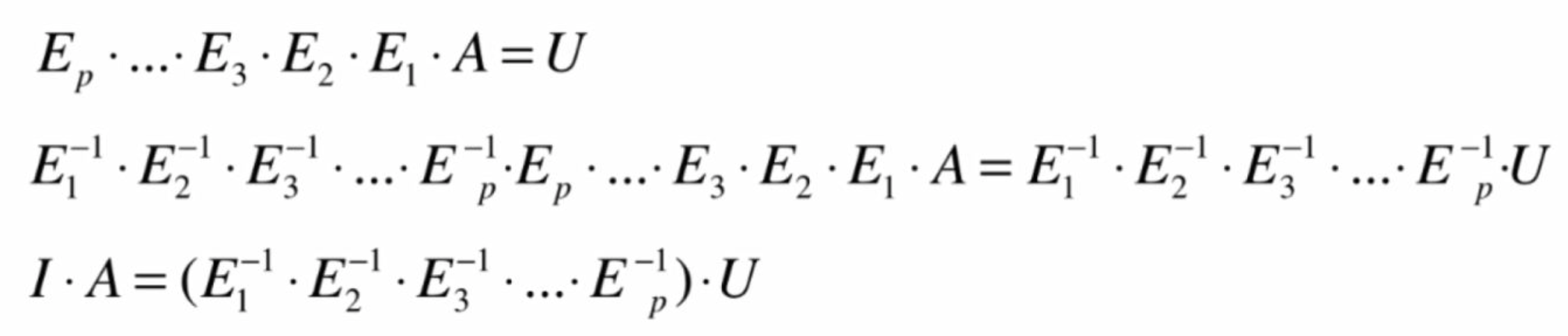
 选主元的LU分解

对于A = LU，我们之前限制了行的互换，选主元的LU分解，只需要把A = LU变成 PA = LU就可以了，其中P是置换矩阵。实际上所有的A = LU都可以写成PA = LU的形式，当A没有行互换时，P就是单位矩阵。

谱分解

A的特征向量q1,q2，Q=[q1 q2]

对角线为特征值其余元素为0 的矩阵B

A=QBQ^T

Cholesky 分解

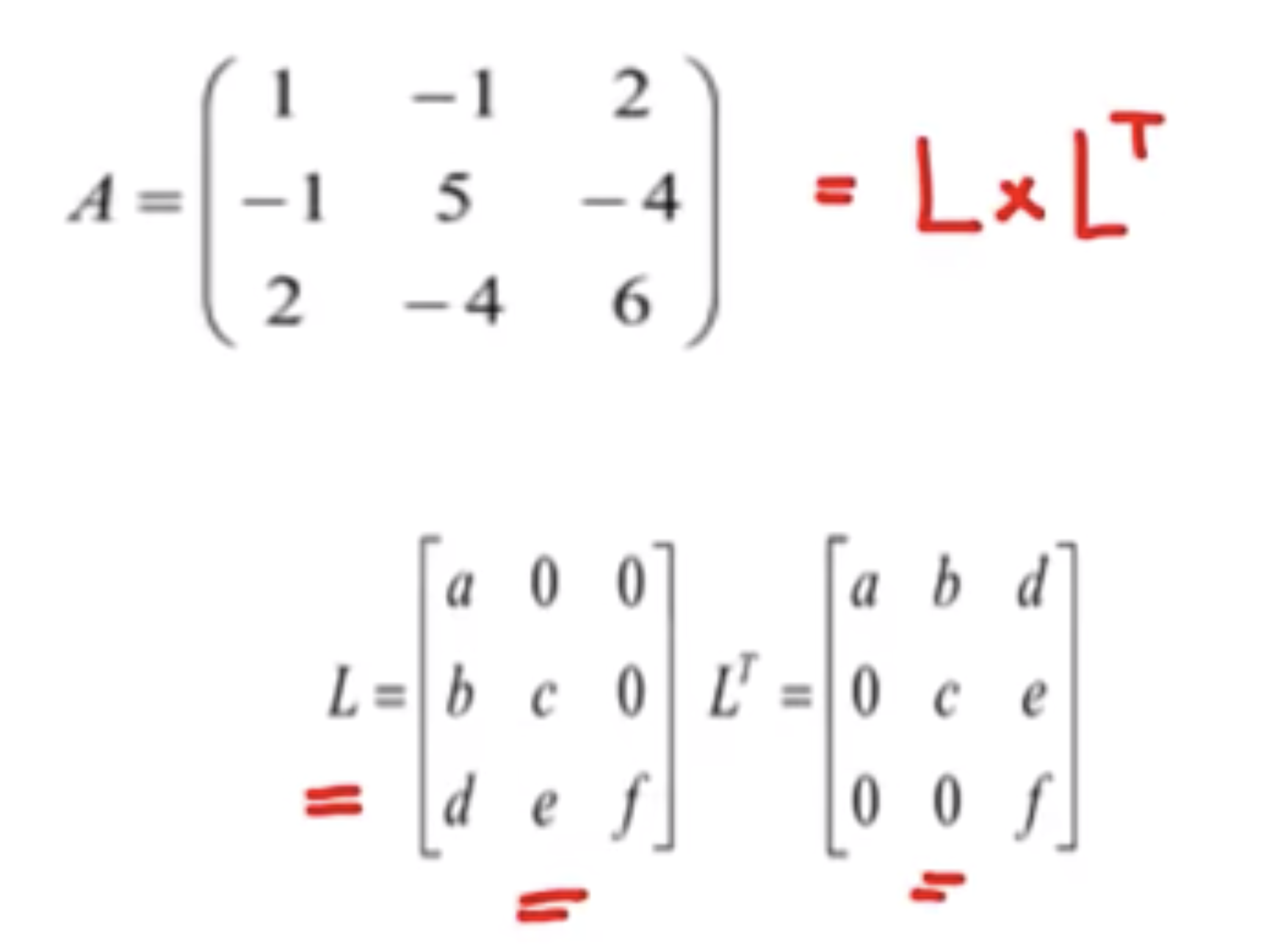
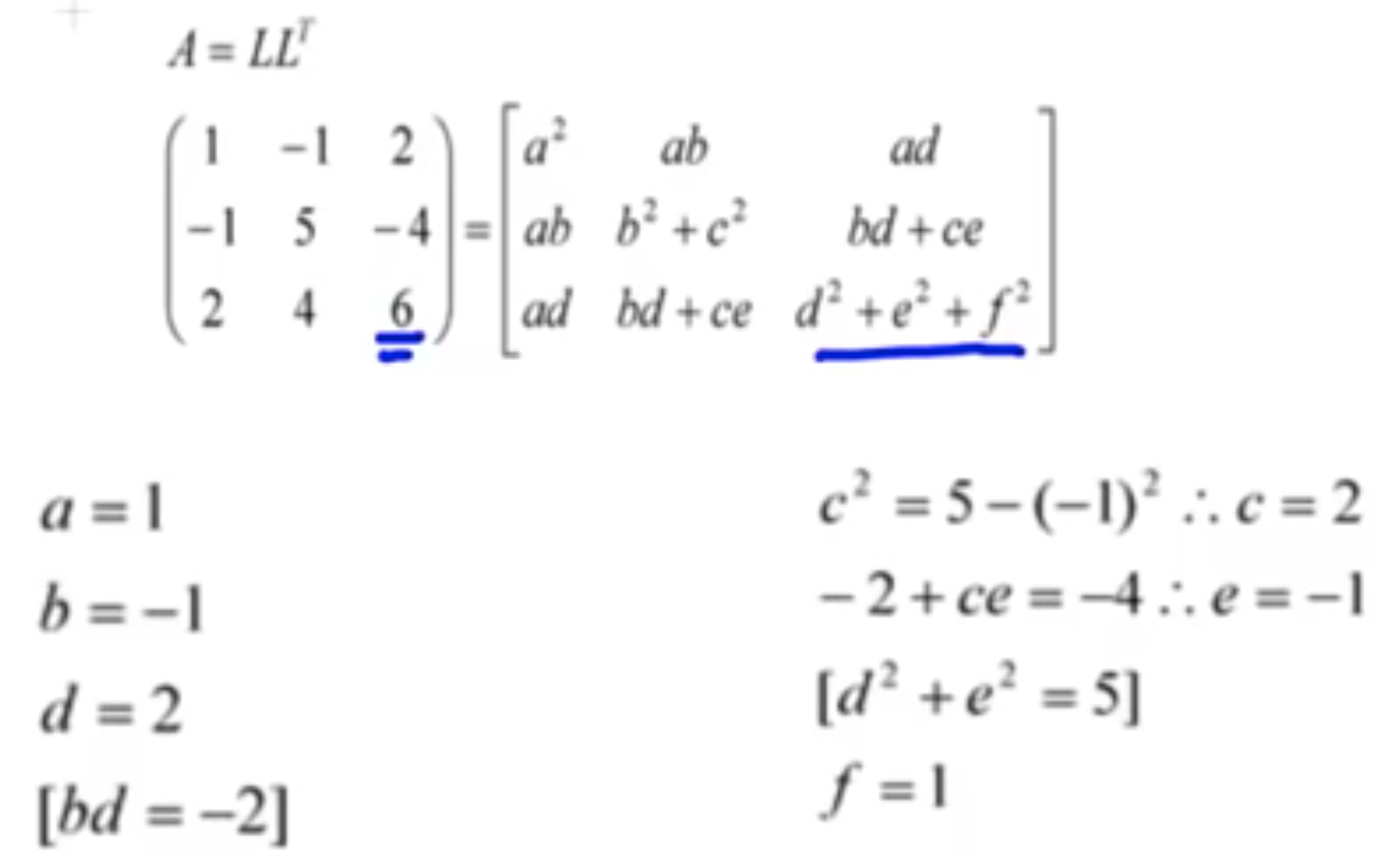
QR分解 

一个矩阵的QR分解是将矩阵分解成A=QR，其中Q是一个正交矩阵（QTQ=I），R是上三角矩阵。

1）基于施密特正交化的QR分解

  具体推导过程可以看我的另一篇博客：https://www.cnblogs.com/wwqdata/p/12889765.html

2）基于householder变换的QR分解

3）基于givens变换的QR分解

 具体分解步骤可参考:https://ccjou.wordpress.com/2010/02/18/givens-%E6%97%8B%E8%BD%89%E6%96%BC-qr-%E5%88%86%E8%A7%A3%E7%9A%84%E6%87%89%E7%94%A8/

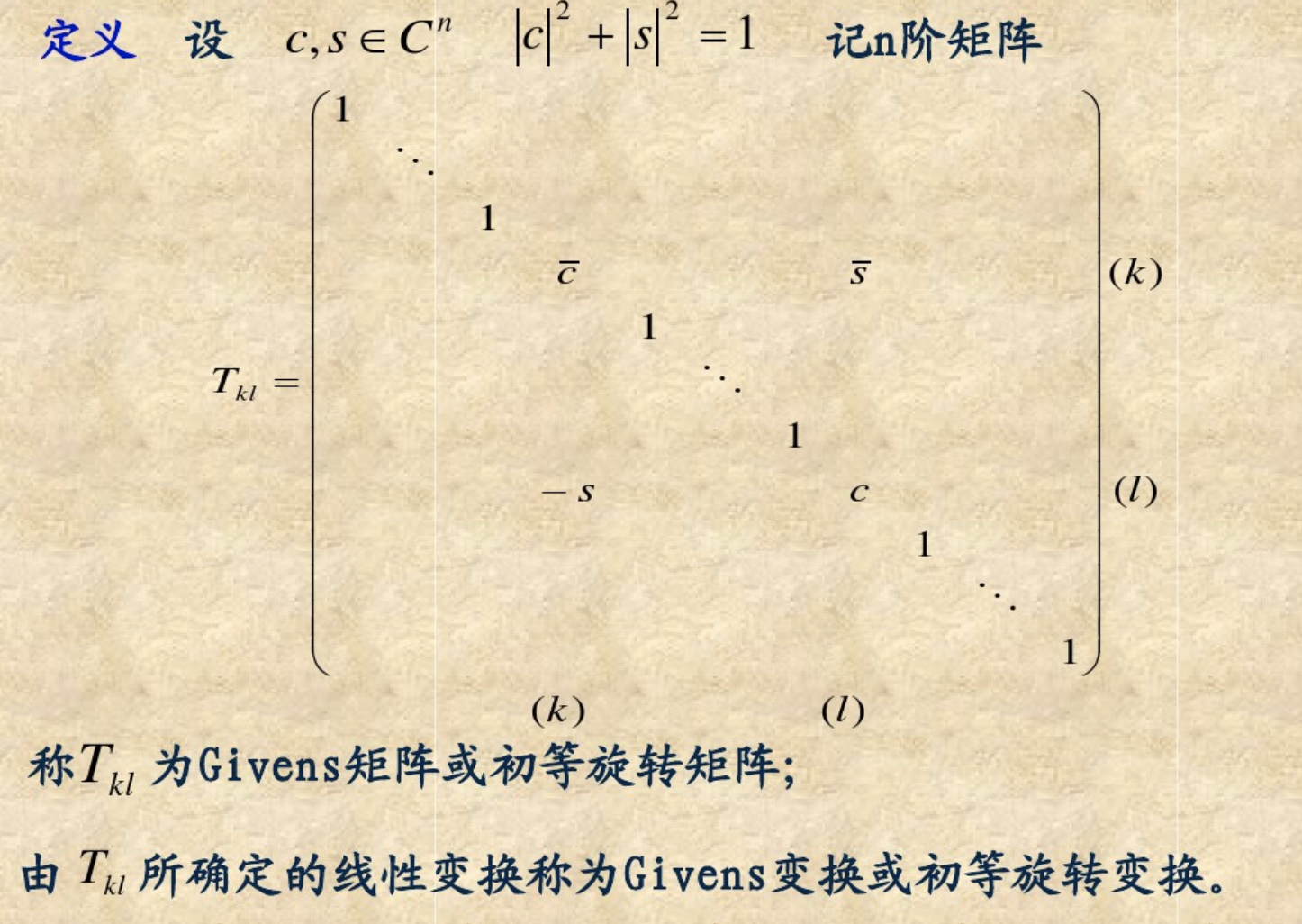
总结一下就是对A分解，先攻A(2,1)元，以A11和A21来确定c 和s，以此确定Q21

然后攻Q21A的(3,1)元，以Q21A的11元和Q21A的31元来确定c 和s，以此确定Q31

最后攻Q31Q21A的(3,2)元

R=Q32Q31Q21A

Q=(Q21)^T(Q31)^T(Q32)^T

SVD分解

见我的另一个博客https://www.cnblogs.com/wwqdata/p/12893876.html