条件期望与重期望法则

重期望法则

 

 

 

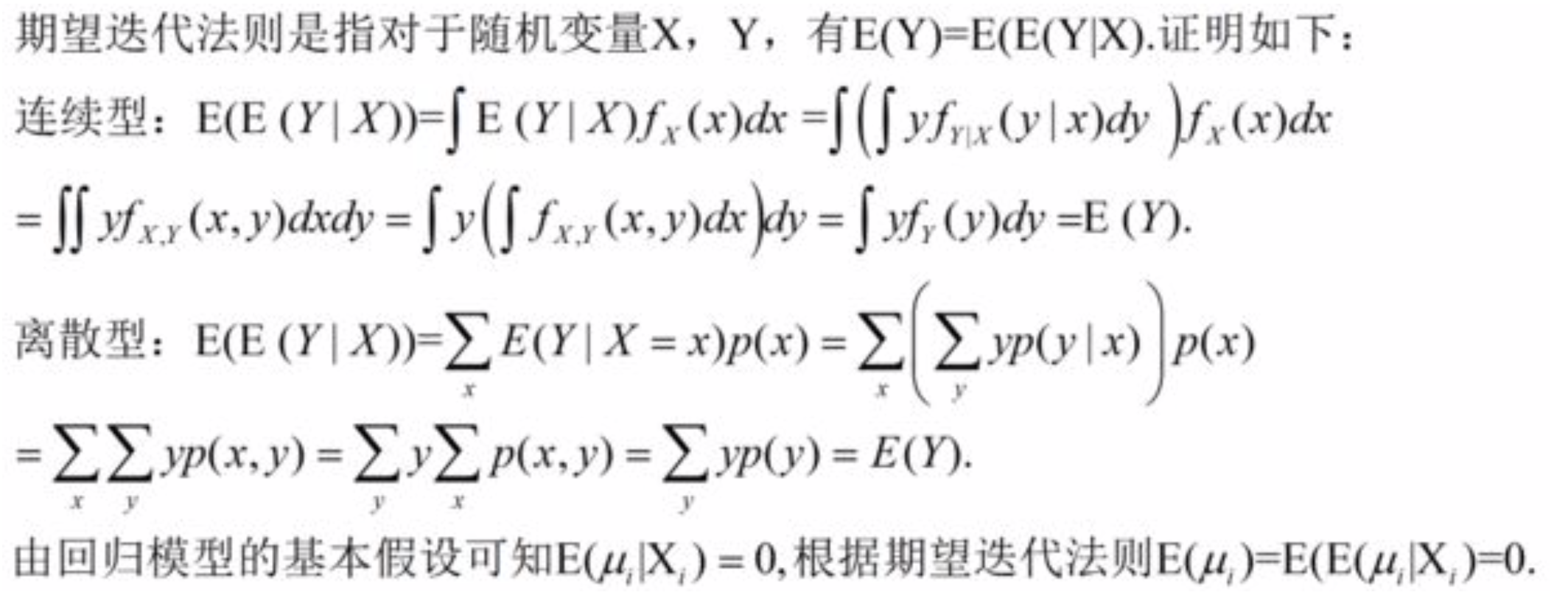
条件期望

 

 

 

期望是对全体的加权平均

条件期望是局限在条件内部的加权平均

对于这个随机变量E(X|Y)，当Y=y时它的取值为E(X|Y=y)，称随机变量E(X|Y)为随机变量X关于随机变量Y的条件数学期望。

由于E(X|Y=y)是一种依赖于Y的分割的局部平均，而EX是全体的平均。把E(X|Y)再平均一次就得到了重期望法则举个例子，如果我们要计算某个年级学生的平均分，有两种方法

    1.可以把该年级每个学生的成绩∑起来，然后再除以总人数，这是极为常规的方法。该方法对应于计算EX；

    2.我们还可以先计算每个班级的平均分（第一次平均），然后在把每个班级的平均分加起来除以班级数（第二次平均）。这便是E(E(X|Y))。这个例子里面，每个班级相当于Y，计算每个班级的平均分相当于固定一个Y=y去求E(X|Y=y)，最后再对班级做平均。
    很显然，用1和2的方法得到的结果是一致的。即E(E(X|Y))=E(X)

先局部平均，再整体平均。
————————————————
参考
：https://blog.csdn.net/henhen2002/article/details/5540039